Big O 표기법

이성은·2022년 11월 11일

Big O

Big O 소개

여러가지 코드를 일반적으로 서로 비교하고 성능을 평가하는 방법
코드를 더 잘 이해하고 더 좋은 코드를 쓰기 위해서 도움이 된다.

코드 시간 재기

예시 코드 : 1부터 숫자n까지 합 구하기
- 예시 코드 1과 2중에 어느 코드가 더 나은가?
더 좋은 better코드는 무엇을 의미하나?
- 더 빠른 코드
  - performance.now()사용
- 많은 메모리 양을 사용하지 않는 효율적인 코드
  => 나머지 고려할 점도 있지만 위에 두개가 제일 중요하다.

//예시 1
function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}
//예시1 코드 실행 시간
let t1 = performance.now();
addUpTo(1000000000);
let t2 = performance.now();
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)
//Time Elapsed: 1.088699999988079 seconds.


//예시2
function addUpTo(n) {
  return n * (n + 1) / 2;
}
//예시2 코드 실행 시간
let t1 = performance.now();
addUpTo(1000000000);
let t2 = performance.now();
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)
//Time Elapsed: 0.00009999999403953553 seconds.

하지만 시간으로 속도를 측정하기엔 문제가 많다.
- 기기 사양에 따라 다를수 있다.
- 같은 기계라도 다른 시간을 기록할수도 있다.
- 빠른 알고리즘에서는 정말 짧은 시간 안에 모든 것이 처리 된다.

=> 빅오 표기법이 필요!!

연산 갯수 세기

컴퓨터가 처리해야하는 연산 갯수를 세기
=> 컴퓨터마다 같다.
예시 코드

//예시 1
function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}
//반복문...=> 많은 연산 갯수...


//예시2
function addUpTo(n) {
  return n * (n + 1) / 2;
}
//곱셉 한개, 덧셈 한개, 나눗셈 한개 => 연산 3개

시간 복잡도

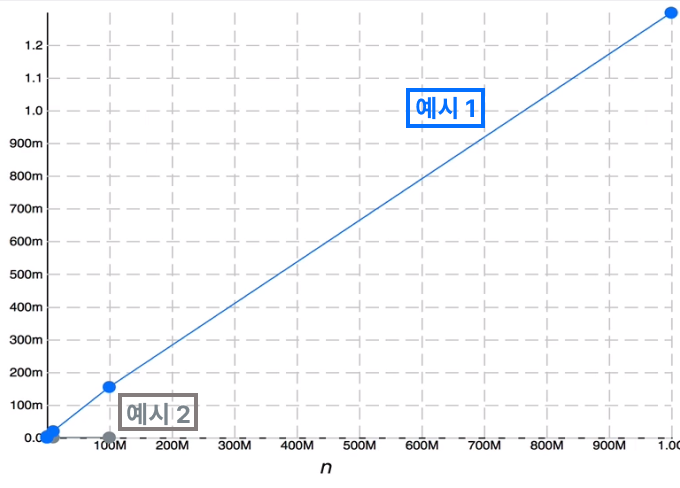
=> 예시1은 n에 따라 연산 시간이 다르지만, 예시2는 n과 상관없이 연산이 항상 3개이므로 시간이 거의같다.

=> 성능으로 보면 예시1과 예시2의 알고리즘이 굉장히 다르다는 것을 볼수 있다.

Big O 란?

입력된 내용이 늘어날 수록 알고리즘에 실행시간이 어떻게 변하는지 설명하는 공식적인 방식
Big O는 어떤 함수의 입력값이 늘어나는 것과 함수의 실행 시간이 변하는 관계를 의미
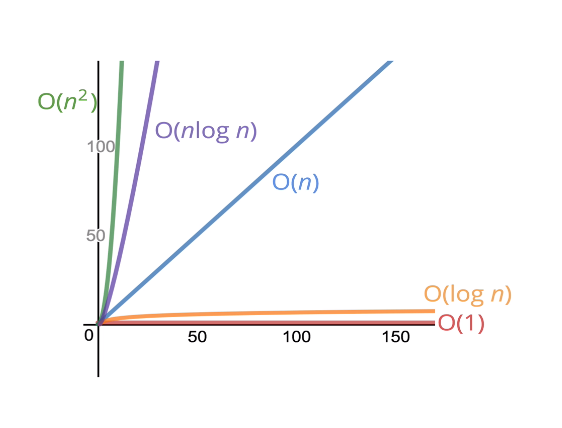
f(n) could be linear (f(n) = n)
- Linear Time (선형)
- 입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘
- n이 1번 늘어날 때마다 처리시간이 1 증가하여 선형적으로 증가
- O(n) 예시
  - 5n이든 3n이든 그냥n이든 그래프는 거의 같다.

//O(n) 예시
function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

f(n) could be quadratic (f(n) = n^2)
- Quadratic Time
- 입력 데이터 n만큼 반복하는데, 그 안에서 n만큼 또 반복할 때의 표기 방법
- 데이터가 적을 때는 문제 없지만 많아질수록 수직상승
  -O(n^2) 예시
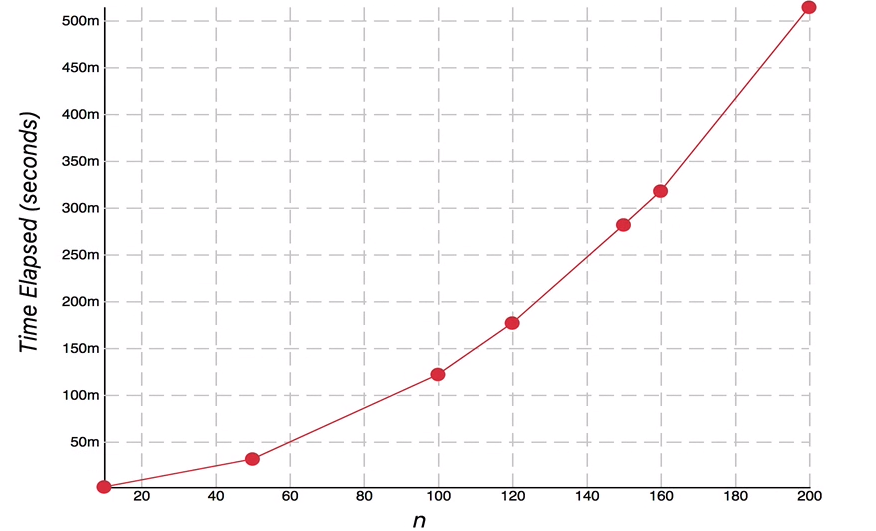
f(n) could be constant (f(n) = 1)
- Constant Time (상수)
- 입력 데이터 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘
- O(1) 예시 => 연산이 항상 3개

// O(1) 예시
function addUpTo(n) {
  return n * (n + 1) / 2;
}

f(n) could be something entirely different!

Big O 표현식의 단순화하기

Big O 표현식의 단순화 예시
- O(2n) => O(n)
- O(500) => O(1)
- O(13n^2) => O(n^2)
- O(n+10) => O(n)
- O(1000n+50) => O(n)
- O(n^2 +5n+8) => O(n^2)
- O(n^2 + n^3) => O(n^3)
Big O 표현식의 단순화
- 산수(덧셈,뺄셈,곱셈,나눗셈)는 상수로 취급
  - 즉 컴퓨터가 2+2를 처리하는 시간이나 100만+2처리하는 시간이나 비슷
- 변수 할당도 상수 취급
  - x=1000이나 x=100만이나 컴퓨터가 변수에 값을 배정하는데 걸리는 시간은 비슷
- 인덱스를 사용해서 배열에 접근하는것, 키값으로 객체에 접근하는 것도 상수 취급
  - 배열에서 첫번째 아이템을 찾던지, 10번째 아이템을 찾던지 인덱스를 사용하면 똑같은 시간이 걸림
- 반복문에서는 복잡도가 반복문 길이 곱하기 반복문 안에 있는 연산들
  - 만약 리스트에 있는 데이터를 반복문으로 처리할때, 0에서 n까지라면, n이 커질수록 반복문의 반복되는 횟수가 늘어나고, 그렇다면 그 반복문안에서 일어나는 연산들도 중요하다. 만약 중첩 반복문이라면 n제곱 실행 시간이 된다.

예시

O(n)

function logAtLeast5(n) {
  for (var i = 1; i <= Math.max(5, n); i++) {
    console.log(i);
  }
}
//logAtLeast5(10) => console.log(i) 10번
//logAtLeast5(1) => console.log(i) 5번
//logAtLeast5(3) => console.log(i) 5번
//반복문이 있어도, 결국 5까지 가거나, n까지 반복
//=> n이 커지면 실행시간은? n=100만이면 반복문도 100만번 반복
//=> 따라서 5는 중요하지 않다. n이 커질수록 연산갯수가 n에 비례해서 늘어난다.

O(1)

function logAtMost5(n) {
  for (var i = 1; i <= Math.min(5, n); i++) {
    console.log(i);
  }
}
//n이 커져도 아무 영향을 주지 않는다.

공간 복잡도(사용되는 메모리)

알고리즘이 공간을 얼마나 필요로 하는지
별도 언급이 없는한, 공간복잡도는 보조 공간 복잡도를 뜻함
booleans, numbers, undefined, null은 자바스크립트에서 불변공간
- 입력의 크기와는 상관없이, 숫자가 1이든 1000이든 모두 불변 공간이라 여긴다.
문자열 : O(n)의 공간이 필요
- 문자열의 길이가 1인 문자열보다 50인 문자열이 더 많은 공간을 차지
reference타입, 배열, 객체인 경우 : O(n)의 공간이 필요
- n은 배열의 길이거나 객체의 키 갯수일수 있다.