학습내용
Basis
벡터 공간 V의 basis는 V라는 공간을 채울 수 있는 선형 관계에 있지 않은 벡터들의 모음
Rank
matrix의 행,열을 이루고 있는 벡터들로 만들 수 있는 공간의 차원
np.linalg.matrix_rank(A)
Span
두 벡터의 조합으로 만들 수 있는 모든 가능한 벡터의 집합
orthogonality
두 벡터가 이루는 각이 수직이면 그 상태를 orthogonality라고 함
- 데이터분석에서 orthogonality의 의미 : 데이터 사이의 각이 수직이라면, 데이터 간의 상관관계가 없다고 해석할 수 있음
Projection vector
특정벡터를 다른 벡터로 전사시킨 벡터
- 데이터분석에서 projection vector의 의미 : 중요 feature 선정을 통한 overfitting 및 모델 복잡도 줄이기
ex. w를 v로 projection
=>
import matplotlib.pyplot as plt
v = [7, 4]
def myProjection(v):
v = np.array(v)
w = np.array([15,15])
v_pro = (np.dot(v,w)/np.dot(w,w))*w
return v_pro
vprime = myProjection(v)
x = np.linspace(0,10,20)
y = x*1
plt.figure(figsize = (7,7))
plt.xlim((0,10))
plt.ylim((0,10))
plt.arrow(0,0,7,4, color='blue', head_width = .2)
plt.plot(x,y, color='red')
plt.arrow(0,0,vprime[0],vprime[1], color = 'green', linestyle ='--', head_width = .2, linewidth = 3)
plt.plot([7,vprime[0]],[4,vprime[1]], color = 'gray', linestyle='--')
plt.show()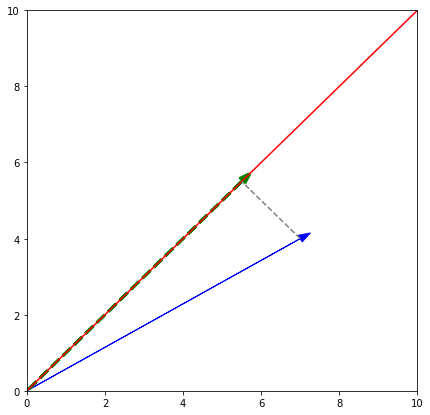
기본통계량
파이썬으로 구현
def mymean(v):
result = 0
for i in v:
result += i
return result/len(v)
def myvar(v): #모분산
dif = np.array(v)-mymean(v)
dif2 = (dif**2).sum()
result = dif2/len(v)
return result
def mystd(v): #모집단의 표준편차
result = np.sqrt(myvar(v))
return result
def myvar2(v): #표본분산
dif = np.array(v)-mymean(v)
dif2 = (dif**2).sum()
result = dif2/(len(v)-1)
return result
def mystd2(v): #표본의 표준편차
result = np.sqrt(myvar2(v))
return resultCovariance
두 변수 간의 선형관계를 나타내는 값
#직접구현
mean1 = mymean(v)
dif1 = np.array(v)-mean1
mean2 = mymean(v2)
dif2 = np.array(v2)-mean2
cov = ((dif1*dif2).sum())/(len(v)-1)
#numpy 사용
np.cov(v1,v2)[0,1]Pearson Correlation
covariance는 데이터의 scale에 의존하는 경향이 있어서 정확한 관계를 이야기하기 어려움. Correlation은 이런 문제를 스케일링을 통해 해결
#직접구현
corr = cov/(mystd2(v)*mystd2(v2))
#numpy 사용
np.corrcoef(v1,v2)[0,1]
#scipy 사용
stats.pearsonr(A,B)
#correlation, p-value 반환Spearman Correlation
categorical data의 단조성을 평가하기 위해 사용됨
단조성이 좋다는 것은 한 변수의 값의 크기가 커지면, 다른 변수의 크기도 커진다는 뜻
from scipy import stats
stats.spearmanr(A,B)
#correlation, p-value 반환matplotlib으로 벡터그리기
벡터 arrow
plt.arrow(x,y, dx,dy, head_width = 0.2, linewidth = 3, color = '')plot과 다른점은 plot은 모든x, 모든y 순으로 데이터가 입력되는데 arrow의 경우 시작점, 끝점의 좌표를 각각 입력으로 넣는다는 점이 다름
3차원
fig = plt.figure()
ax = fig.gca(projection='3d')
X = [0,0,0]
Y = [0,0,0]
Z = [0,0,0]
l = [1,2,3]
m = [-1,0,7]
n = [4,8,2]
ax.set_xlim(-1,10)
ax.set_ylim(-1,10)
ax.set_zlim(-1,10)
ax.quiver(X,Y,Z,l,m,n, color=['red','blue','green'])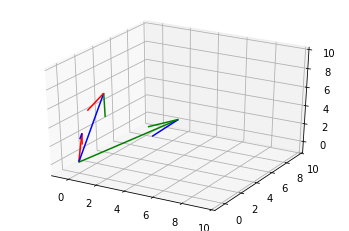
알아보기 : matplotlib에서의 gca, plt.subplots,np.meshgrid
