학습내용
Vector transformation
선형변환 : 임의의 두 벡터를 더하거나 스칼라 값을 곱하는 것을 의미
행렬의 곱을 벡터의 변환 측면에서 바라보는 습관을 길러보자
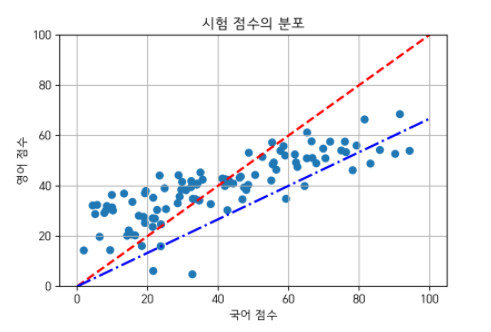
그림출처 : https://angeloyeo.github.io/2019/07/27/PCA.html
위의 그림과 같이 국어와 영어 점수를 직선 위의 점으로 변환시키는 과정도 선형 변환이라고 할 수 있음
Eigenvector
transformation에 영향을 받지 않는 축(주축), 즉 주어진 transformation에 대해서 크기만 변하고 방향은 변화하지 않는 벡터
Eigenvalue
고유벡터가 변화하는 스칼라 값
PCA
feature를 줄여 overfitting을 막기 위한 방법
-
핵심 원리 : 공분산 행렬의 고유 벡터는 데이터가 어떤 방향으로 분산되어 있는지를 나타내준다. 이를 이용하여 특정 데이터들의 주성분을 찾아내는 방법
-
eigen vector에 정사영한 데이터들의 variance는 eigenvalue가 됨을 수학적으로 증명가능
-
따라서 몇개의 eigenvalue를 이용하여(어떤 차원으로) PCA 하느냐에 따라 기존데이터를 설명하는 정도(%)가 달라짐. 기존 데이터의 90%를 설명하고 싶으면
가 0.9가 넘는 m을 선택
import seaborn as sns
#pca 파이썬 실습
cols = ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']
idx = ['species']
df = sns.load_dataset('penguins')
df.index = df['species']
df = df[cols]
df.head()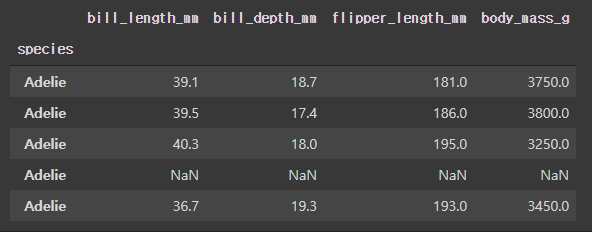
from sklearn.preprocessing import StandardScaler, Normalizer
from sklearn.decomposition import PCA
scaler = StandardScaler()
Z = scaler.fit_transform(df)
print('Scale data : \n',Z)
pca = PCA(2)
pca.fit(Z)
print('\n Eigenvectors : \n', pca.components_)
print('\n Eigenvalues : \n', pca.explained_variance_)
print('\n Explained variance ratio : \n', pca.explained_variance_ratio_)
#pca.explained_variance를 통해서 직접 계산가능
ratio = pca.explained_variance_ratio_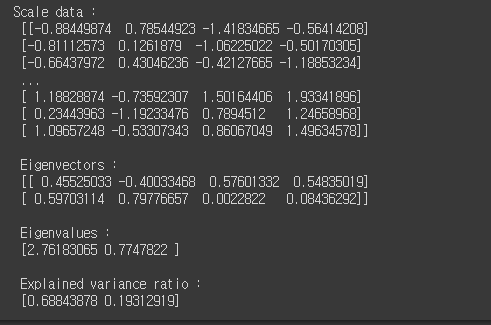
import pandas as pd
B = pca.transform(Z)
df_Z = pd.DataFrame(B, columns = ['trans_X', 'trans_Y'], index = df.index)
df_Z.reset_index(inplace=True)
p = sns.scatterplot(
x='trans_X',
y='trans_Y',
data=df_Z,
hue='species'
);
p.set_title('species');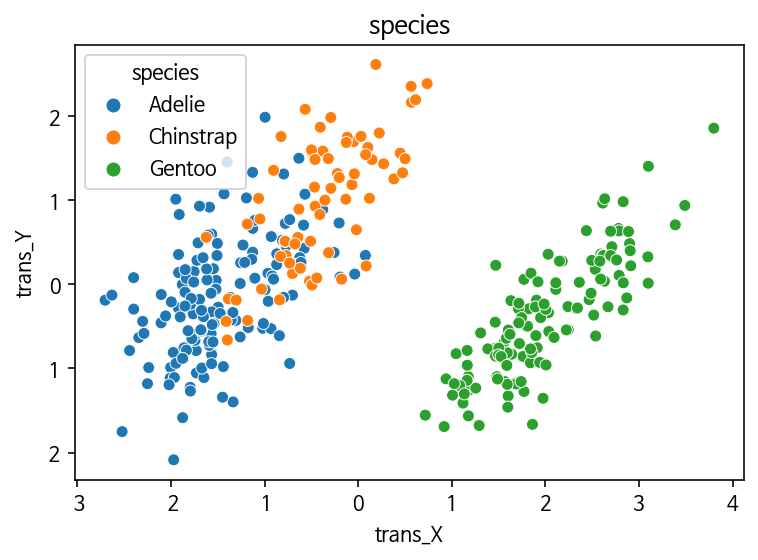
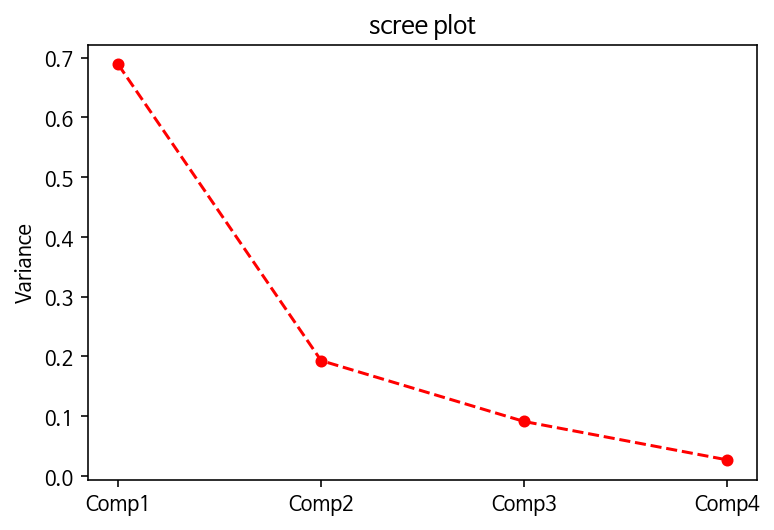
#scree plot
pca3 = PCA(4)
pca3.fit(Z)
ratio3 = pca3.explained_variance_ratio_
plt.plot(
['Comp1', 'Comp2', 'Comp3', 'Comp4'],
[ratio3[k] for k in range(0, 4)],
marker = 'o', #marker 참고 시 : matplotlib 공식 사이트
linestyle = '--',
color = 'r',
markersize = '5'
)
plt.ylabel('Variance')
plt.title('scree plot')
plt.show()