분할정복을 이용한 알고리즘

학습내용

Divide and Conquer(분할 정복)

복잡하거나 큰 문제를 여러 개로 나눠서 푸는 방법

• 재귀와의 차이

  • 재취호출은 같은 함수코드를 재호출하는 것
  • 분할정복은 비슷한 작업을 재진행하는 것

  # 재귀 : 1부터 10까지의 합
  def func(num):
    if num < 1:
      return 0
    else:
      return num + func(num-1)
  
  func(10)
  
  
  # 분할정복 : 1부터 10까지의 합
  def func(num):
    if num == 1:
        return 1
    if num % 2 == 1:
        return func(num - 1) + num
    else:
        return func(num / 2) * 2 + (num / 2) * (num / 2) 
  
  func(10)

퀵정렬, 병합정렬

• 퀵정렬

  • 피봇을 정한다.
  • 피봇을 기준으로 작은 것들은 왼쪽으로, 큰 것들은 오른쪽으로 배치한다.
  • 피봇의 위치는 정해지고 왼쪽 오른쪽으로 분할된 배열들에 대해 재귀적으로 앞의 과정을 반복한다.
  • 순환 호출이 진행될 때마다 최소한 하나의 원소(피봇)의 위치가 정해진다.
  

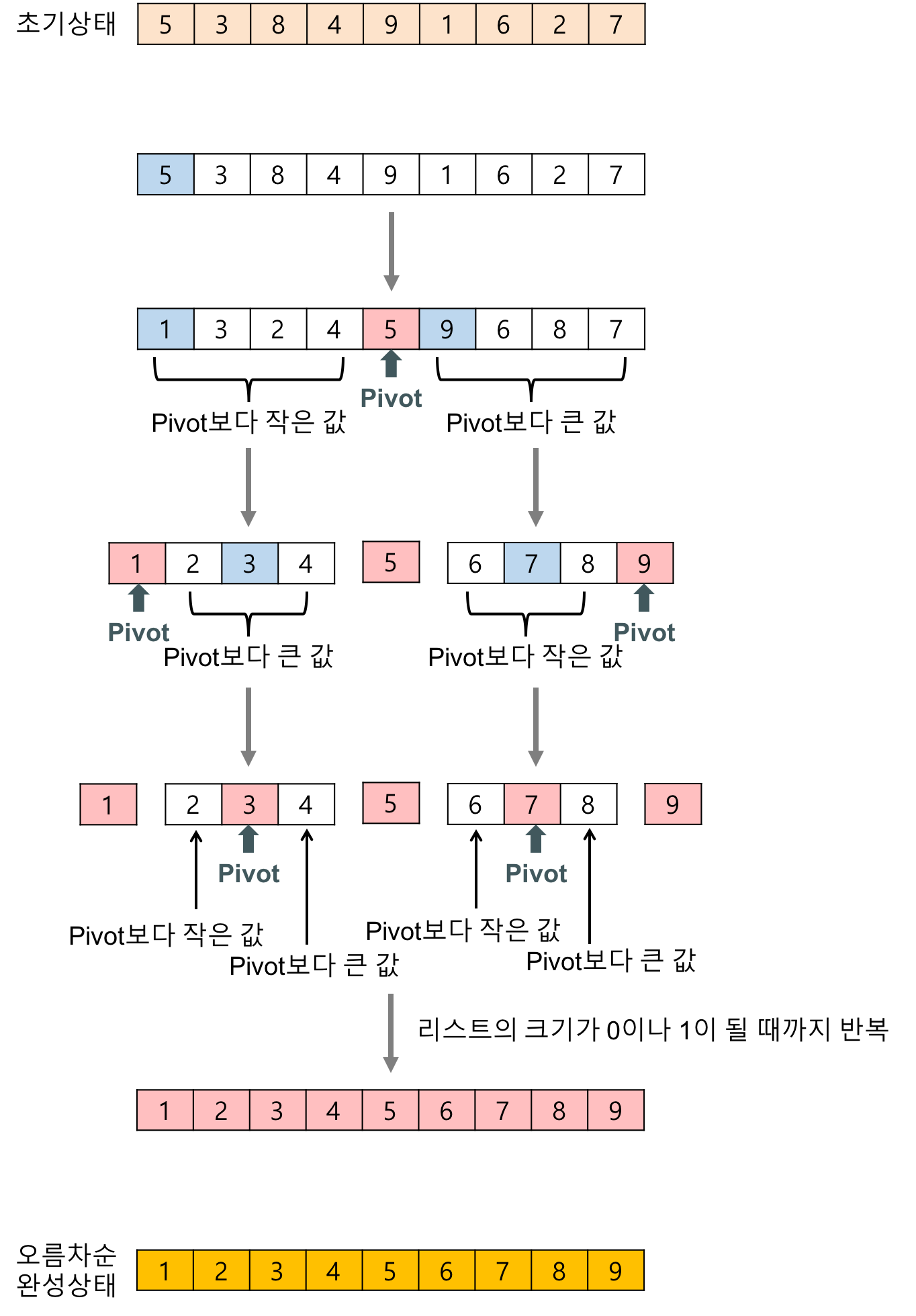
  ​ 출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html

  • 병합정렬에 비해 빠르다.
  • 불안정 정렬
  • 시간 복잡도 : O(nlogn)

  # 퀵소트 파이썬 코드 case - 1 : 전체코드
  
  def quick_sort(node, first, last):
    def partition(first,last):
      pivot = node[last]
      left = first
      #left는 pivot보다 작은 node들의 위치를 나타내는데 사용, 작은 노드들이 right를 통해 발견되면 한칸씩 늘려감
      
      #print(pivot, first,last)    # 확인용
      for right in range(first, last): #right는 피봇을 제외한 모든 노드를 순회하기 위해 사용
        if node[right] < pivot:
          node[left], node[right] = node[right], node[left]
          left += 1
      node[left], node[last] = node[last], node[left]
      return left
  
    # 첫번째 노드가 마지막 노드보다 작은 경우, 재귀진행
    if first < last:
      pivot = partition(first, last)
      quick_sort(node, first, pivot - 1)
      quick_sort(node, pivot + 1, last)
  
  
  node = [54,26,93,17,77,31,44,55,20]
  quick_sort(node,0,8)
  
  print(node)

• 병합정렬

  • 배열을 반으로 divide
  • 1개의 노드만 남을때까지 앞의 과정을 반복
  • 나누어진 노드들을 sort하며 merge
  

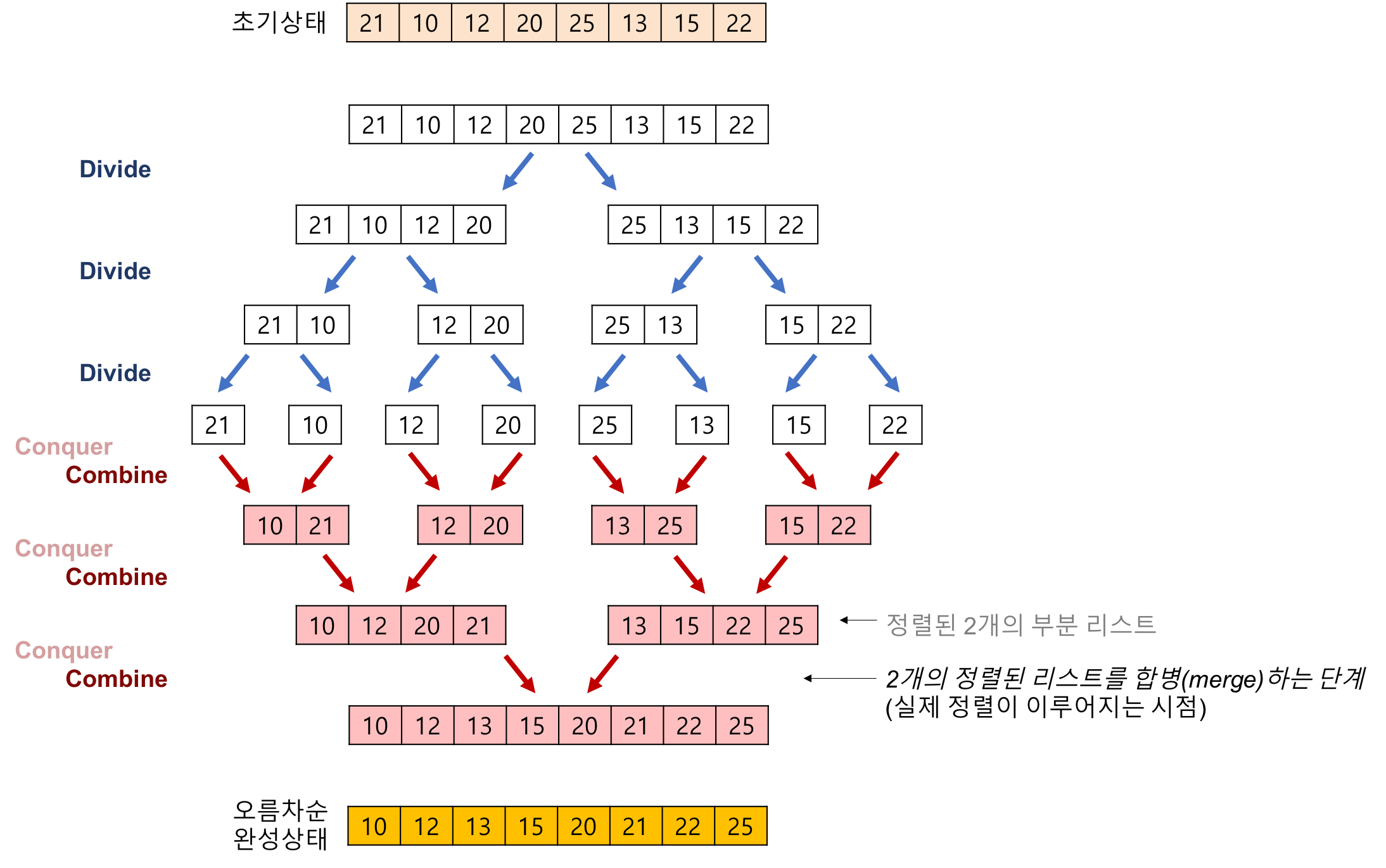
  ​ 출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html

  • 퀵정렬에 비해 느리다.
  • 안정 정렬
  • 시간 복잡도 : O(nlogn)

메모이제이션

분할된 서브문제를 해결하기 위해, 반복되는 해결법을 재사용하는 기법

계산결과를 저장한다.

# 메모이제이션을 적용한 경우

memo = {}    # 재사용을 값을 저장하기 위한 딕셔너리 변수

def recursive_factorial(n):
    if n is 0:
        return 1
    elif n in memo:
        return memo[n]   # 메모이제이션
    else:
        result = n * recursive_factorial(n - 1)
        memo[n] = result
        return result

# 1번째 케이스
print("recursive_factorial(5):",recursive_factorial(5)," memo:", memo)

# 2번째 케이스
print("recursive_factorial(4):",recursive_factorial(4)," memo:", memo)