학습내용
SWAP
파이썬에서의 swap
-
# 첫번째 방법 a = 3 b = 1 temp = a a = b b = temp print(a,b) -
# 두번째 방법 a = 3 b = 1 a, b = b, a # 파이썬에서는 한 줄로 변경가능 print(a,b)
Search algorithm basic
-
선형 검색
- 한 번에 하나씩 모두 검색하는 방법
- 시간 복잡도 : O(n)
def linear_search(linear_arr, search_number): for i in range(len(linear_arr)): if linear_arr[i] == search_number: return i linear_arr = [5,22,87,1,3] search_number = 1 print("search index : ",linear_search(linear_arr, search_number)) -
이진 검색
- 반복을 통해 숫자를 반으로 줄이면서 검색
- 이미 정렬된 경우에만 작동
- 시간 복잡도 : O(log n)
def binary_search(test_list, search_item): low = 0 high = len(test_list) - 1 while low <= high: middle = (low + high) // 2 # middle을 지정해서 검색속도를 빠르게 한다. guess = test_list[middle] if guess == search_item: return middle if guess > search_item: high = middle - 1 else: low = middle + 1 return None
Iterative Sorting
-
selection sort(선택정렬)
- 가장 작은 노드를 선택
- 가장 왼쪽에 있는 노드와 비교하며 교환
- 앞의 두 과정을 반복

- 시간 복잡도 : O(n^2)
- 안정적이지않음 : 중복이 있을 경우, 원래 순서 유지가 안됨
- 실제 예시 : 도서관 책 정리
# 선택정렬 소스코드 def selection_sort(items): for i in range(0, len(items) - 1): # 외부 반복문(루프) cur_index = i smallest_index = cur_index for j in range(cur_index + 1, len(items)): # 내부루프 # 최소값찾는 로직 if items[smallest_index] > items[j]: smallest_index = j # swap items[smallest_index], items[cur_index] = items[cur_index], items[smallest_index] return items
-
Insertion sort(삽입정렬)
- 특정 노드를 이미 정렬된 배열과 비교
- 특정 노드보다 작은 값을 갖고 있는 노드가 나올때까지 비교를 진행
- 작은 값의 노드가 발견되면 그 오른쪽 인덱스에 특정 노드를 삽입
- 아직 정렬이 되지않은 노드 중 하나를 골라 앞의 과정을 반복
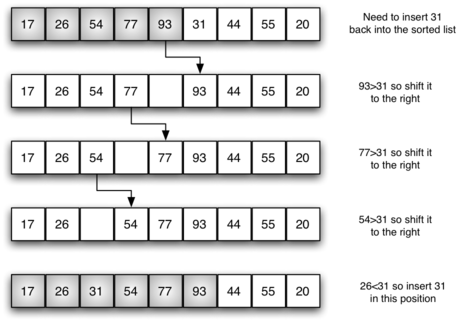
출처 : https://runestone.academy/runestone/books/published/pythonds/SortSearch/TheInsertionSort.html
- 소량의 데이터를 정렬하기 위한 효율적인 알고리즘
- 시간 복잡도 : O(n^2)
# 삽입정렬 소스코드 def ins_sort(unsort_list): loop_number = len(unsort_list) # 반복횟수를 위한 길이설정 # 앞쪽에 있는 노드들을 검색하기 위한 반복문 for compare_index in range(loop_number): # 비교하려는 위치부터 loop_number만큼 반복 compare_value = unsort_list[compare_index] prev_position = compare_index - 1 # 이전 노드값에 대한 인덱스를 가리킴 # 비교연산 후 삽입을 진행하는 반복문 while prev_position >= 0 and unsort_list[prev_position] > compare_value: # 1-1차작업 : swap을 위한 작업 unsort_list[prev_position], unsort_list[compare_index] = unsort_list[compare_index], unsort_list[prev_position] prev_position = prev_position - 1 # 1-2차작업 : 비교된 더 큰 값을 (이전노드+1) 인덱스에 삽입 compare_index = compare_index - 1 return unsort_list test_arr = [5,3,1,6] ins_sort(test_arr)
-
Bubble sort(버블정렬)
- 서로 이웃한 두 원소의 크기를 비교한 결과에 따라 교환을 반복하는 알고리즘
- 첫 번째 항목부터 마지막 항목까지 두개씩 짝지어 비교하고, 대소에 따라 교환

- 시간 복잡도 : O(n^2)
- 이웃노드만 교환하므로 안정적임
버블정렬 소스코드 def bubble_sort(li): length = len(li) - 1 for i in range(length): for j in range(length-i): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] # 외부 반복문(아래 그림에서 전체 리스트에 대해 정렬이 완료되었는지 검사하고 패스해줌) # 내부 반복문(아래 그림에서 하나의 리스트의 개별 값을 비교하고 교체시킨다) # 현재 인덱스의 값과 다음 인덱스의 값 비교 # 비교한 것에 따라 정렬을 위한 인덱스 교환 작업 li = [10, 2, 1, 7, 4, 3, 0] bubble_sort(li) print(li)
