Python Scaler

BodeulMaNN·2023년 4월 10일
python
0

데이터를 모델링 하기전 반드시 스케일링 과정을 거친다.
스케일링을 통해 다차원의 값들을 비교분석하기 쉽게 만들고, 자료의 오버플로우나 언더플로우를 방지(과적합, 과소적합)하고, 독립변수의 공분산 행렬의 조건수를 감소시켜 최적화 과정에서의 안정성 및 수렴속도를 향상시킨다.

특히 kmeans 등 거리 기반의 모델에서는 스케일링이 매우 중요하다.

조건수

작은 변화의 비율에 대해 함수가 얼마나 변화할 수 있는지 에 대한 argument measure이다.

조건수가 크면 약간의 오차만 있어도 해가 전혀 다른 값을 가진다. 따라서 조건수가 크면 회귀분석을 사용한 예측값도 오차가 커지게 된다.

회귀분석에서 조건수가 커지는 경우는 크게 두 가지가 있다.

1) 변수들의 단위 차이로 인해 숫자의 스케일이 크게 달라지는 경우. 이 경우에는 스케일링(scaling)으로 해결한다.

2) 다중 공선성 즉, 상관관계가 큰 독립 변수들이 있는 경우, 이 경우에는 변수 선택이나 PCA를 사용한 차원 축소 등으로 해결한다.

스케일링의 종류

  1. StandardScaler
  2. MinMaxScaler
  3. MaxAbsScaler
  4. RobustScaler
  5. Normalizer()
  1. StandardScaler
from sklearn.preprocessing import StandardScaler
standardScaler = StandardScaler()
print(standardScaler.fit(train_data))
train_data_standardScaled = standardScaler.transform(train_data)

  • 평균을 제거하고 데이터를 단위 분산으로 조정한다. 그러나 이상치가 있다면 평균과 표준편차에 영향을 미쳐 변환된 데이터의 확산은 매우 달라지게 된다.

  • 각 feature에서 평균값을 빼고, 분산을 1로 만드는 형태의 표준화 기법이다.

  • 스케일링보다 표준화에 가깝다.

  • 로버스트스케일러와 마찬가지로 미리 정의된 간격에 의해 데이터 변형이 이루어지지 않으므로, 엄격한 스케일링이 아니다.

  • 딥러닝 알고리즘은 평균이 0이면서 단위분산의 분포를 가진 데이터의 입력을 필요로 할 때가 있다.(특히 회귀모델)

  • 스탠다드 스케일러는 각 feature들 사이에 상대적 거리를 왜곡시킬 수 있는 단점이 있으므로, 다른 형태의 표준화 기법과 비교해서 주로 차선책으로 활용된다.

  • 따라서 이상치가 있는 경우 균형 잡힌 척도를 보장할 수 없다.

  1. MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
minMaxScaler = MinMaxScaler()
print(minMaxScaler.fit(train_data))
train_data_minMaxScaled = minMaxScaler.transform(train_data)

  • 모든 feature 값이 0~1사이에 있도록 데이터를 재조정한다. 다만 이상치가 있는 경우 변환된 값이 매우 좁은 범위로 압축될 수 있다.

  • 각 feature들에서 최소값을 빼고, 전체 범위로 나눈다. 범위는 데이터의 최대값에서 데이터의 최소값을 뺀 값이 된다.

  • 본래 데이터의 분포를 유지시키며 정보를 변형시키지 않는 장점이 있으나, 이상치의 영향을 줄이지 못한다.

  • 본래 데이터의 정규본포를 변형시키고 싶지 않거나, 이상치의 영향을 그대로 보고 싶으면 가장 먼저 시도해볼 수 있는 방법이다.

  • 계산된 값들은 0~1사이의 범위로 축소된다.

  • 즉, MinMaxScaler 역시 아웃라이어의 존재에 매우 민감하다.

  1. MaxAbsScaler

절대값이 0~1사이에 매핑되도록 한다. 즉 -1~1 사이로 재조정한다. 양수 데이터로만 구성된 특징 데이터셋에서는 MinMaxScaler와 유사하게 동작하며, 큰 이상치에 민감할 수 있다.

from sklearn.preprocessing import MaxAbsScaler
maxAbsScaler = MaxAbsScaler()
print(maxAbsScaler.fit(train_data))
train_data_maxAbsScaled = maxAbsScaler.transform(train_data)
  1. RobustScaler

아웃라이어의 영향을 최소화한 기법이다. 중앙값(median)과 IQR(interquartile range)을 사용하기 때문에 StandardScaler와 비교해보면 표준화 후 동일한 값을 더 넓게 분포 시키고 있음을 확인 할 수 있다.

  • MinMaxScaler와 비슷하지만 미리 정해진 간격에 의해 데이터를 변형시키지 않는다.

  • 엄격한 스케일링이아니며 이상치의 효과를 줄이기에 MinMaxScaler보다 적합하다.

  • 각 feature값에서 중간 값을 빼고, IRQ 범위로 나눈 것을 말한다. (IRQ = 75%의 값 — 25%의 값)

IQR = Q3 - Q1 : 즉, 25퍼센타일과 75퍼센타일의 값들을 다룬다.

아웃라이어를 포함하는 데이터의 표준화 결과는 아래와 같다. 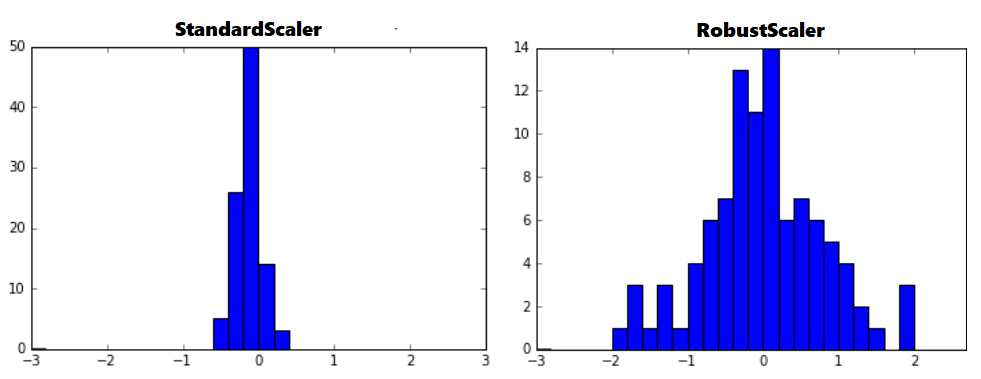img_area

from sklearn.preprocessing import RobustScaler
robustScaler = RobustScaler()
print(robustScaler.fit(train_data))
train_data_robustScaled = robustScaler.transform(train_data)
  1. Normalizer()

  • 앞의 4가지 방법은 각 피처(feature)의 통계치를 이용합니다. 즉, 열(columns)를 대상으로 합니다.

  • 그러나 Normalizer 의 경우 각 행(row)마다 정규화가 진행됩니다.

  • 이는 한 행의 모든 피처들 사이의 유클리드 거리가 1이 되도록 데이터값을 만들어줍니다.

  • 이렇게 하면 좀 더 빠르게 학습할 수 있고 과대적합 확률을 낮출 수 있다고 합니다.

  • 각 feature의 열이 아닌 행에 값이 적용된다.

  • Normalizer의 총합은 1이된다. 모든 값은 -1과 1 사이의 범위 안에 놓인다.

from sklearn.preprocessing import Normalizer

norm = Normalizer()
X_train_scaled = norm.fit_transform(X_train)
X_test_scaled = norm.transform(X_test)
dtc.fit(X_train_scaled, y_train)
print('모델의 정확도 :', round(dtc.score(X_test_scaled, y_test), 4))

결론적으로 모든 스케일러 처리 전에는 아웃라이어 제거가 선행되어야 한다. 또한 데이터의 분포 특징에 따라 적절한 스케일러를 적용해주는 것이 좋다.

데이터 분포별 변환 결과

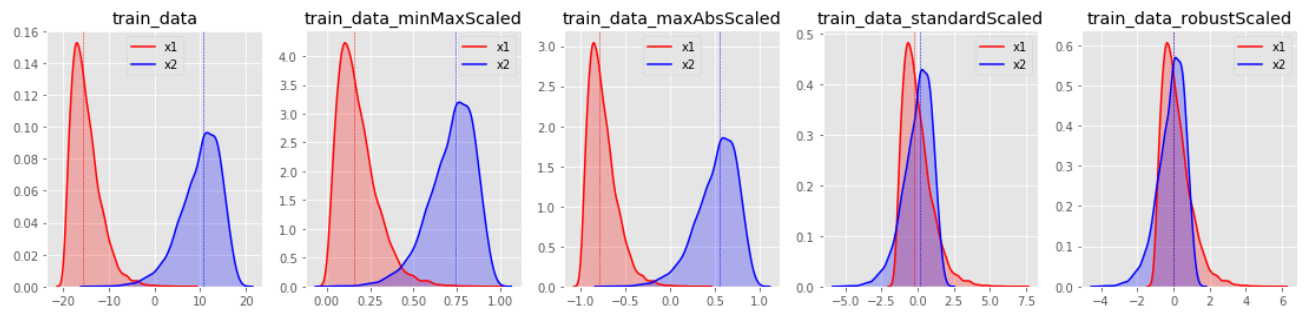
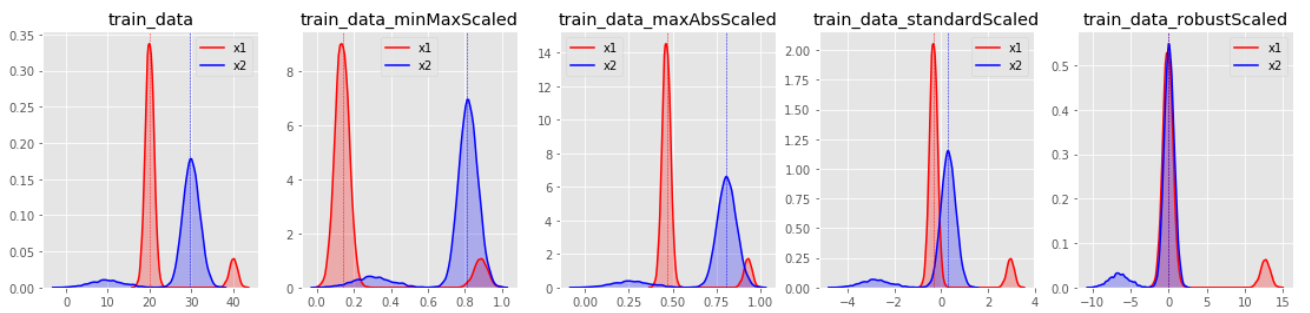
img_area img_area img_area img_area img_area

변환 분포를 살펴보면 StandardScaler와 RobustScaler의 변환된 결과가 대부분 표준화된 유사 형태의 데이터 분포로 반환된다.

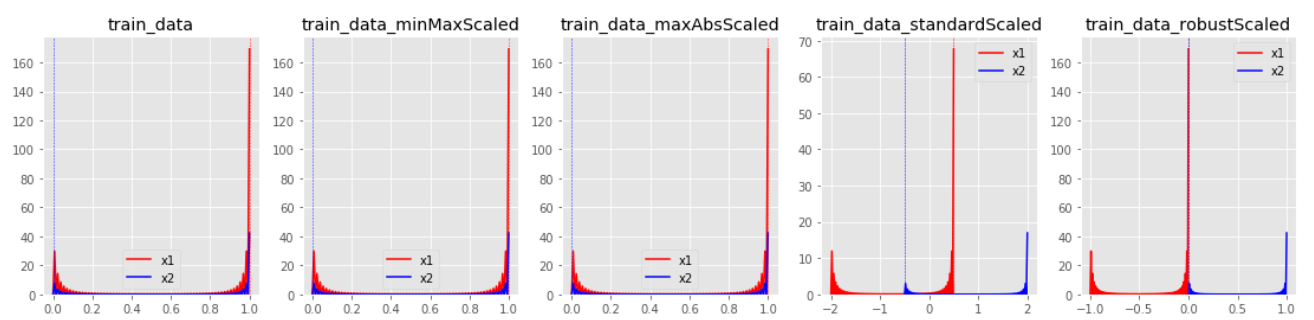
MinMaxScaler특정값에 집중되어 있는 데이터가 그렇지 않은 데이터 분포보다 1표준편차에 의한 스케일 변화값이 커지게 된다. 한쪽으로 쏠림 현상이 있는 데이터 분포는 형태가 거의 유지된채 범위값이 조절되는 결과를 보인다.

MaxAbsScaler의 경우, MinMaxScaler와 유사하나 음수와 양수값에 따른 대칭 분포를 유지하게 되는 특징이 있다.

그리고 마지막 이미지를 통해 살펴보면, 대부분의 스케일링 기법에서 아웃라이어는 변환 효과를 저해하는 요소임이 드러난다.

유의해야할 점은, 스케일링시 Feature별로 크기를 유사하게 만드는 것은 중요하지만, 그렇다고 모든 Feature의 분포를 동일하게 만들 필요는 없다.

특성에 따라 어떤 항목은 원본데이터의 분포를 유지하는 것이 유의할 수 있다. 예로 데이터가 거의 한 곳에 집중되어 있는 Feature를 표준화시켜 분포를 같게 만들었을때 작은 단위의 변화가 큰 차이를 나타내는 것으로 반영될 수 있기 때문이다.

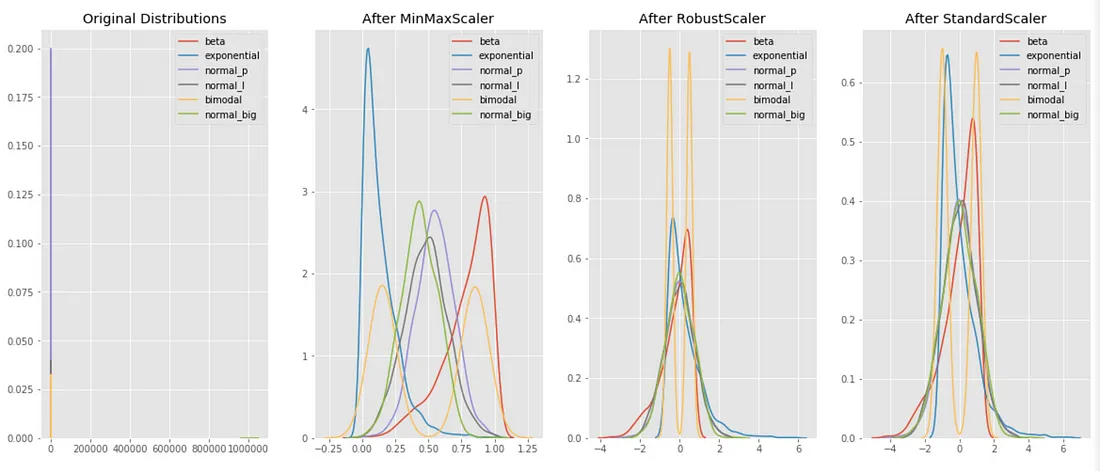
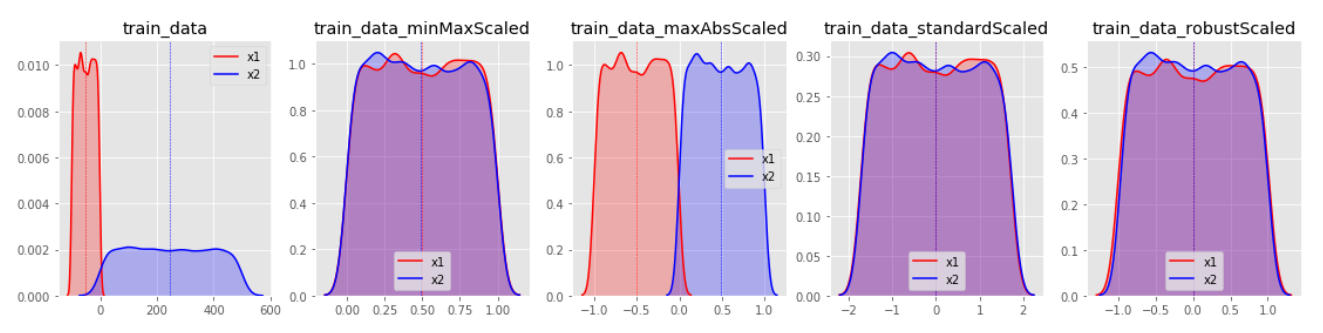
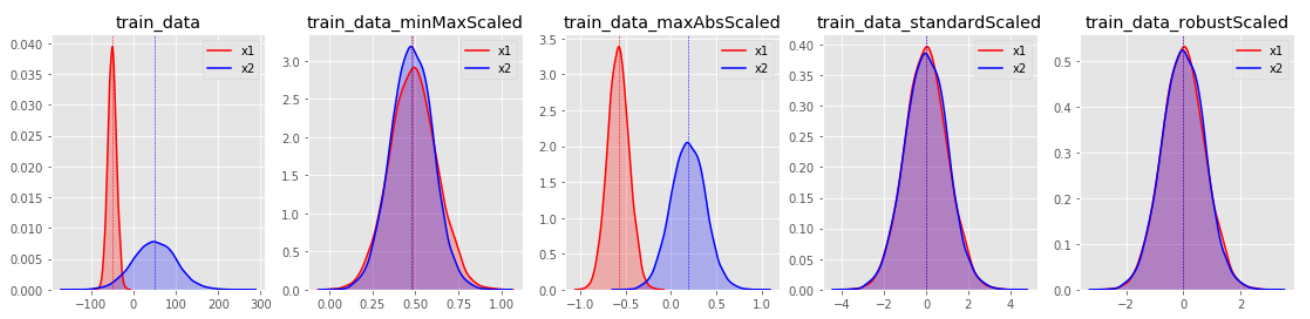
본래 데이터의 분포와, 3가지의 기법을 적용했을 때의 분포를 각각 비교한 모습
본래 데이터의 분포와 비교해 보면, 3가지의 표준화 기법이 대부분 비슷한 스케일로 데이터들의 분포를 조정한 것을 볼 수 있다. MinMaxScaler는 각 feature들 사이의 거리를 왜곡하지 않는다는 점을 눈여겨 보라. 바로 이러한 특징이, MinMaxScaler가 데이터의 분포와 이상치의 영향을 온전이 보기 위해 가장 많이 사용되는 이유일 것이다. 반대로 분포보다, 이상치의 영향이 얼마나 줄었는지를 보고 싶다면 RobustScaler가 더 유용할 것이다. 또한, 모든 데이터를 정규분포화(normal distribution)하여 보고 싶다면 StandardScaler가 가장 유용할 것이다.

요약

  • 데이터의 왜곡이 없이 순수하게 분포를 비교하고 싶을 때는 MinMaxScaler 사용
  • 이상치가 있고, 그 영향을 줄이고 싶다면 RobustScaler 사용 — 그러나 이상치는 없애는 것이 가장 좋다.
  • 모든 데이터의 분포를 정규분포로 보고 싶다면 StandardScaler를 사용
    Normalizer에는 L1과 L2기법이 있다. 데이터의 열(columns)이 아닌 행(row)에 사용되므로 사용에 주의가 필요하다.

참고문헌)
https://mkjjo.github.io/python/2019/01/10/scaler.html
https://conanmoon.medium.com/%EB%8D%B0%EC%9D%B4%ED%84%B0%EA%B3%BC%ED%95%99-%EC%9C%A0%EB%A7%9D%EC%A3%BC%EC%9D%98-%EB%A7%A4%EC%9D%BC-%EA%B8%80%EC%93%B0%EA%B8%B0-%EC%97%AC%EC%84%AF%EB%B2%88%EC%A7%B8-%EC%9D%BC%EC%9A%94%EC%9D%BC-b3f2992c5ffd

profile
BodeulMaNN
반갑습니다
이전 포스트

Python 분류모형의 종류

다음 포스트

Python Scaler

0개의 댓글

관련 채용 정보