📌 1. The perceptron
🔸 이전에 배운 모델에서는 로직 연산은 가능하지만 실제 뉴런에서 나타나는 신호가 지속적으로 들어와 threshold를 넘었을 때 출력을 내보내는 모델은 포함하지 않았음
🔸 입력 노드는 x1, x2, x3
1. Simple model (Frank Rosenblatt)
🔸 thresholding 동작을 하는 unit을 포함하는 모델 생성
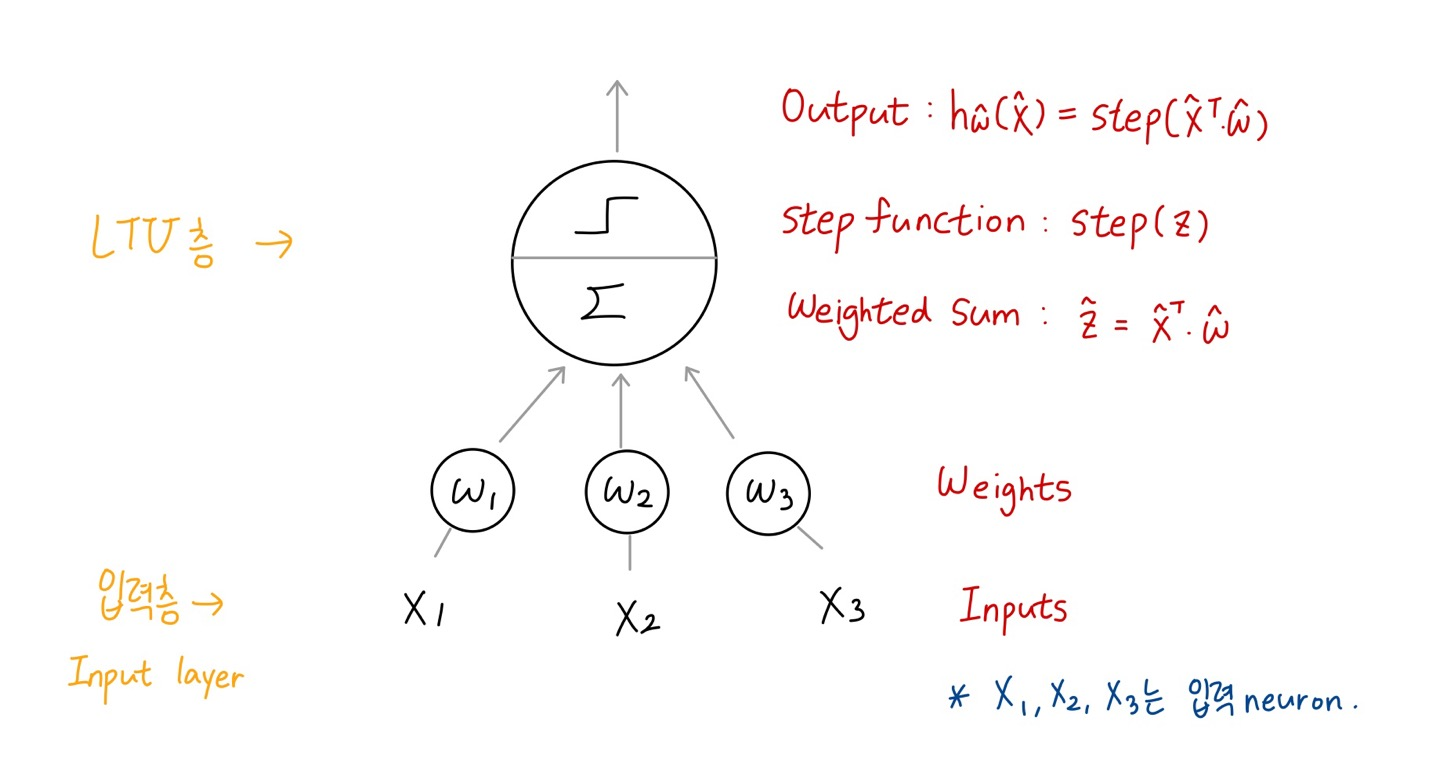
1) Linear threshold unit(LTU): the inputs and output are now numbers (instead of binary values) and each input connection is associated with a weight
🔸 이전에 배운 모델에서는 input으로 0과 1의 binary 값만 가져올 수 있었는데 Rosenblatt에서는 input과 output으로 임의의 값 numbers을 가질 수 있음
🔸 각각의 input은 가중치 weight를 가지고 들어오도록 설계
weight
: 입력값이 들어올 때 가중치를 가지고 들어오면서 x1w1이 입력으로 돌아옴
ex. w1이 1일 경우 x1이 들어가고, w1이 0.5일 경우 x1의 절반에 해당하는 값이 들어가고, w1이 2일 경우 x1의 2배에 해당하는 값이 들어감
2) z = w1x1 + w2x2 + ... + wnxn = w^T * x
🔸 z는 weighted sum으로 output 함수에 들어갈 값
🔸 w1x1은 w1과 x1의 곱
vector로 표현하면 w^T와 x의 scalar product
3) applies a step function: hw(x) = step(z) = step(w^T * x)
🔸 input은 number지만, step function을 거친 출력값 output은 반드시 0 또는 1 혹은 -1 또는 0 또는 1
🔸 step function 종류
1. heaviside function
output이 0 또는 1
2. sign function
output이 -1 또는 0 또는 +1
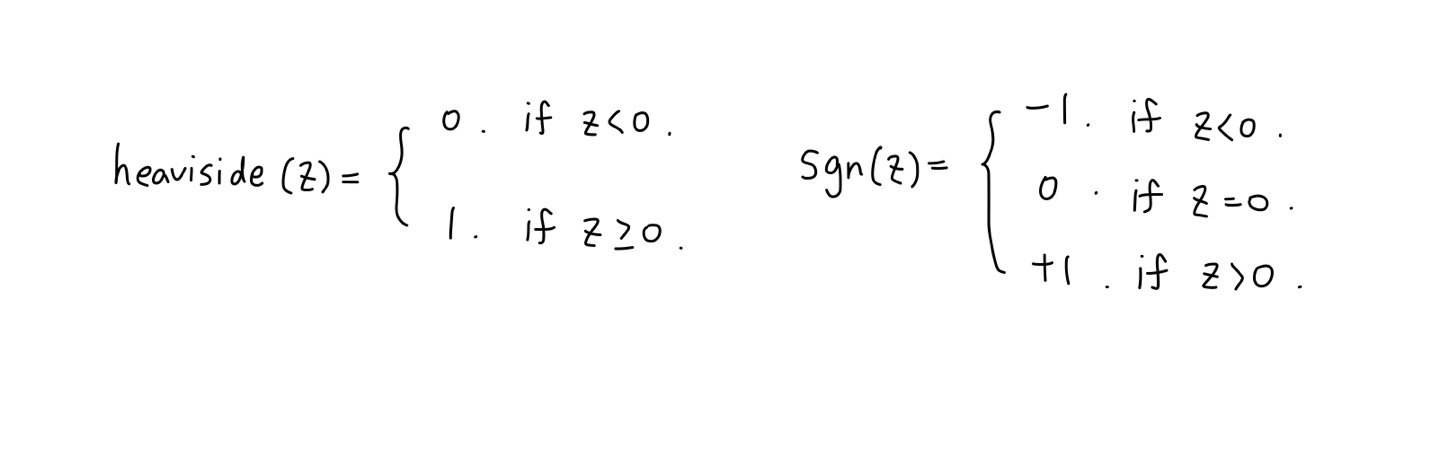
4) positive class for above threshold; otherwise, negative class
🔸 (heaviside function 사용 기준) binary classification 사용할 경우, threshold보다 클 경우 positive class(1 출력), 아닐 경우 negative class(0 출력)
5) Ex. Iris classification based on the petal length and width
6) Training LTU: finding the right values for w1,w2, and w3
🔸 LTU를 학습시킨다는 것은 정확한 weight w1,w2,w3를 찾는 것
🔸 학습이 완료된 LTU는 고정된 weight를 가지고 새로운 x1,x2,x3가 입력으로 들어가면 weighted sum을 구해 step function을 거쳐 output을 출력
2. Single layer LTUs
🔸 LTU를 한 층만 사용
1) Fully connected (or dense) layer
🔸 입력층과 LTU는 fully connected layer를 가짐
2) Input neuron: feed inputs
🔸 input neuron이 input값을 넣어줌
🔸 input layer에서 x1,x2,x3가 입력 neuron
3) Bias neuron: outputs 1 all the time
🔸 입력과는 별개로 1이라는 값을 가진 항상 고정된 뉴런 존재
🔸 입력처럼 모든 LTU에 입력으로 추가됨
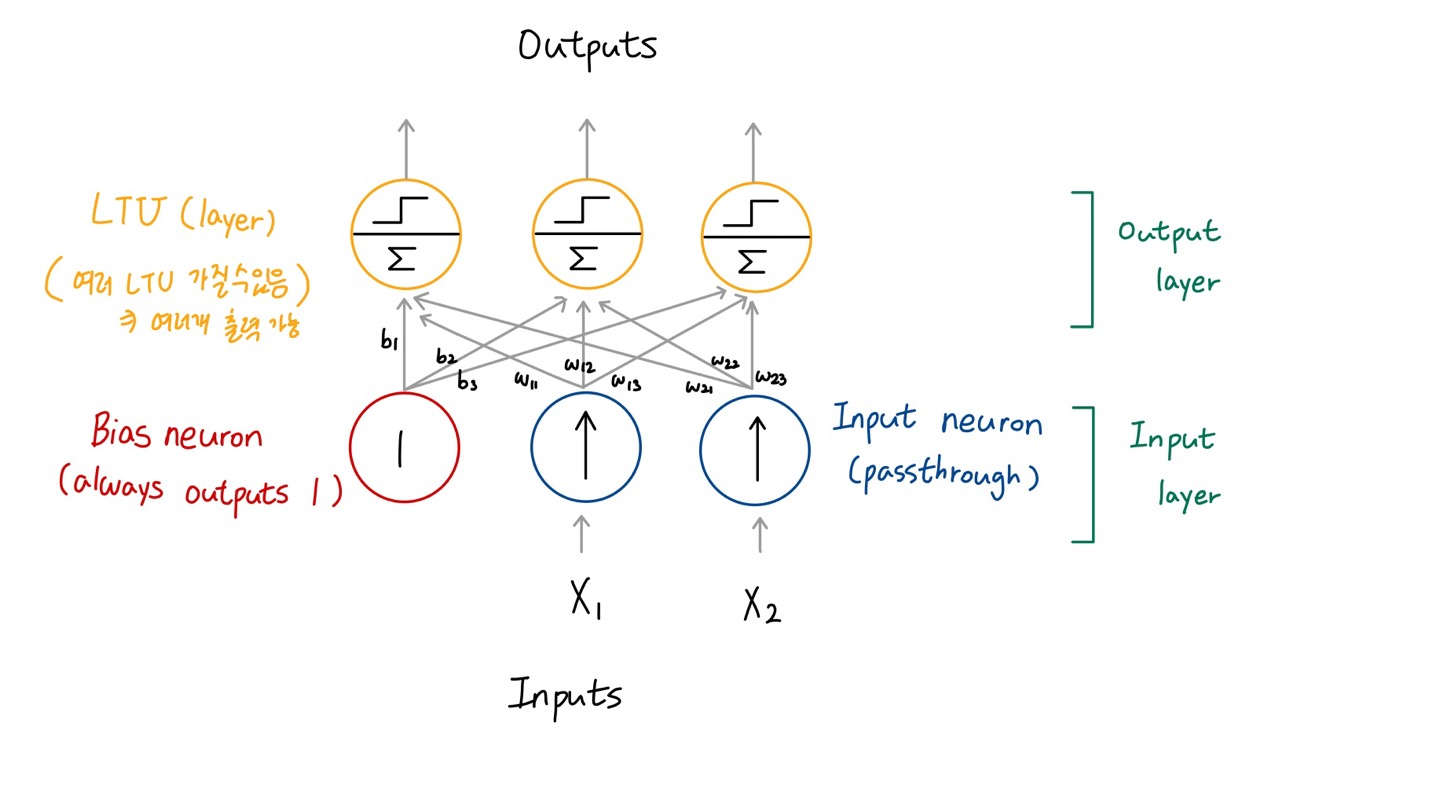
🔸 input layer는 입력값(X1,X2)과 bias neuron으로 구성. 입력이 n개면 입력 layer는 bias neuron까지 포함해 총 (n+1)개의 neuron 가짐
🔸 fully connected라는 것은 각각의 입력 neuron(입력뉴런에 bias는 포함X)이 모든 LTU layer에 입력을 공급 + bias도 모든 LTU layer에 입력 공급, Input layer의 모든 노드가 LTU layer의 모든 노드가 서로 모두 연결 => fully connected network
🔸 multi-output : LTU layer에 뉴런이 여러개 존재 => 여러 개의 출력 가능
4) Multi-output classifier
🔸 위 그림 사용
ex. two inputs and three outputs
🔸 동시에 3개의 class 구분가능
🔸 만약 output에 1이 여러개 존재할 경우, 3개의 class가 아니라 LTU 각각이 별개의 binary classifier로 사용한것
🔸 Perceptron을 수학적 모델로 표현한 것
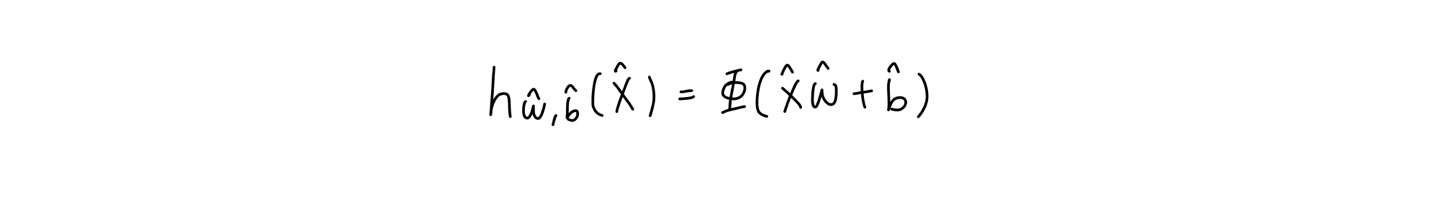
🔹 XW+b는 앞에서 말한 z를 의미
🔹 b는 bias neuron에 주어지는 가중치
🔹 pi가 activation function이고 heaviside 또는 sign function이 될 수도 있음
💡 LTU 하나가 perceptron
💡 perceptron을 학습시킨다는 것은 적절한 w와 b값을 찾는것
📌 2. Perceptron training
🔸 Perceptron training은 적절한 w와 b값을 찾는 것
1. Inspired by Hebbian learning (or Hebb's rule)
Connection weight between two neurons is increased whenever they have the same output
🔸 두 가지 neuron이 같은 output을 가질 때 weight 증가
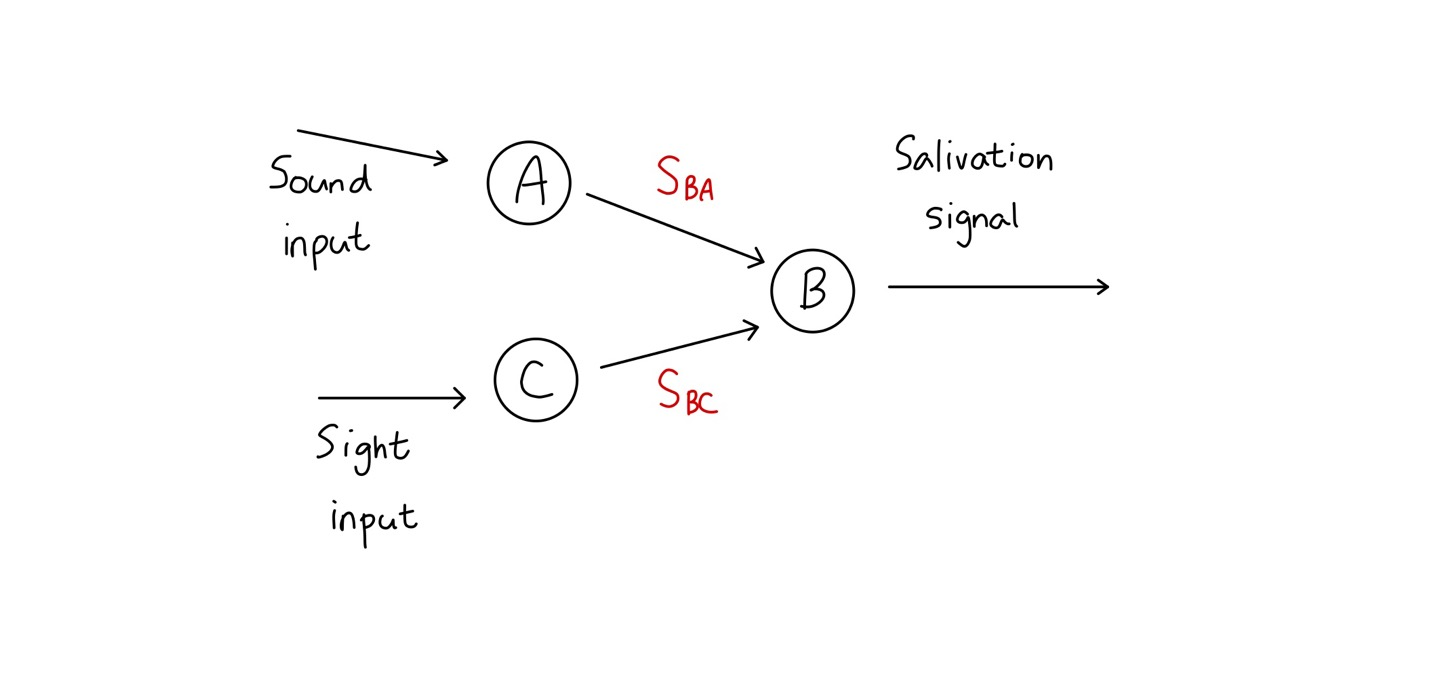
🔸 Sound input은 처음에 Sba라는 weight를 가짐. 학습을 진행하면서 Sba는 점점 커져 결과적으로 sound(input)만 들려도 salivation(output) 출력
2. Perceptron trianing
1) Takes into account the error made by the network
🔸 네트워크에서 만들어진 오류 고려
2) One training instance at a time, and makes its predictions for each instance
🔸 train 입력값을 한 번에 하나 넣고, perceptron network에서 각 instance마다 출력값(prediction)을 얻기
3) For every output neuron with a wrong prediction
🔸 정답을 알고있는 데이터에 대해 학습진행
🔸 학습 초기에는 잘못된 prediction값이 나올 가능성 높음
-
reinforces the connection weights of the inputs for the correct prediction
🔸 하나의 output neuron에는 여러개의 입력이 들어옴
🔸 잘못된 prediction이 나왔지만, 정확한 prediction이 나오도록 기여한 입력의 weight 강화 -
decrease error
🔸 학습이 진행되면서 error 값이 줄어들어 최종적으로 대부분의 입력 instance에 대해 올바른 prediction을 하도록함

🔸 오차를 줄이는 방향으로 w값 변화시킴
3. Decision boundary is linear
🔸 Decision boundary: prediction이 올바른지 아닌지 판단하는 기준
🔸 Perceptron의 decision boundary가 linear하기 때문에 perceptron은 복잡한(nonlinear한) 문제를 해결할 수 없음
ex. Iris classification using Perceptron
4. Code_Scikitlearn의 Perceptron을 이용한 Iris classification model
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:, (2,3)] #petal length, petal width
y = (iris.target == 0).astype(np.int) #Iris Setosa?
per_clf = Pereptron(random_state = 42)
per_clf.fit(X,y)
y_pred = per_clf.predict([[2, 0.5]])🔸 perceptron은 tensorflow 사용하지 않아도 scikitlearn에 포함된 모델 이용해 사용 가능
5. Perceptron learning algorithm: strongly resembles Stochastic Gradient Descent
🔸 Same as SGDClassifier with the following hyperparameters: loss="perceptron", learning_rate="constant",eta0=1 (the learning rate), and penalty=None(no regularization)
6. No class probability; just make predictions based on a hard threshold (0/1)
Logistic Regression preffered
🔸 hard threshold에 따라 출력이 0 또는 1만 나옴. 어떤 확률로 positive, negative가 결정되는지는 알 수 없음.
🔸 probability 원한다면 logistic regression 사용
