📌 Multi-Layer Perceptron(MLP)
🔸 기존의 perceptron은 nonlinear한 문제 해결 불가능. BUT Multi-layer로 perceptron을 구성하면 nonlinear한 문제 해결 가능
1. Perceptrons are incapable of solving some trivial problems
🔸 기존의 perceptron은 nonlinear한 문제 해결 불가능
=> 복잡한 문제뿐만 아니라 간단한 문제도 nonlinear하면 해결할 수 없음
1) Exclusive OR(XOR) classification problem (Marvin Minsky and Seymour Papert, 1969)
:간단한 nonlinear한 문제 예시. perceptron으로 해결 불가능
🔸 feature space
사각형과 삼각형 두 개의 class에 해당하는 instance 아래와 같이 존재. Linear problem의 경우 하나의 직선(Decision boundary)으로 분류할 수 있어야함 => 불가능
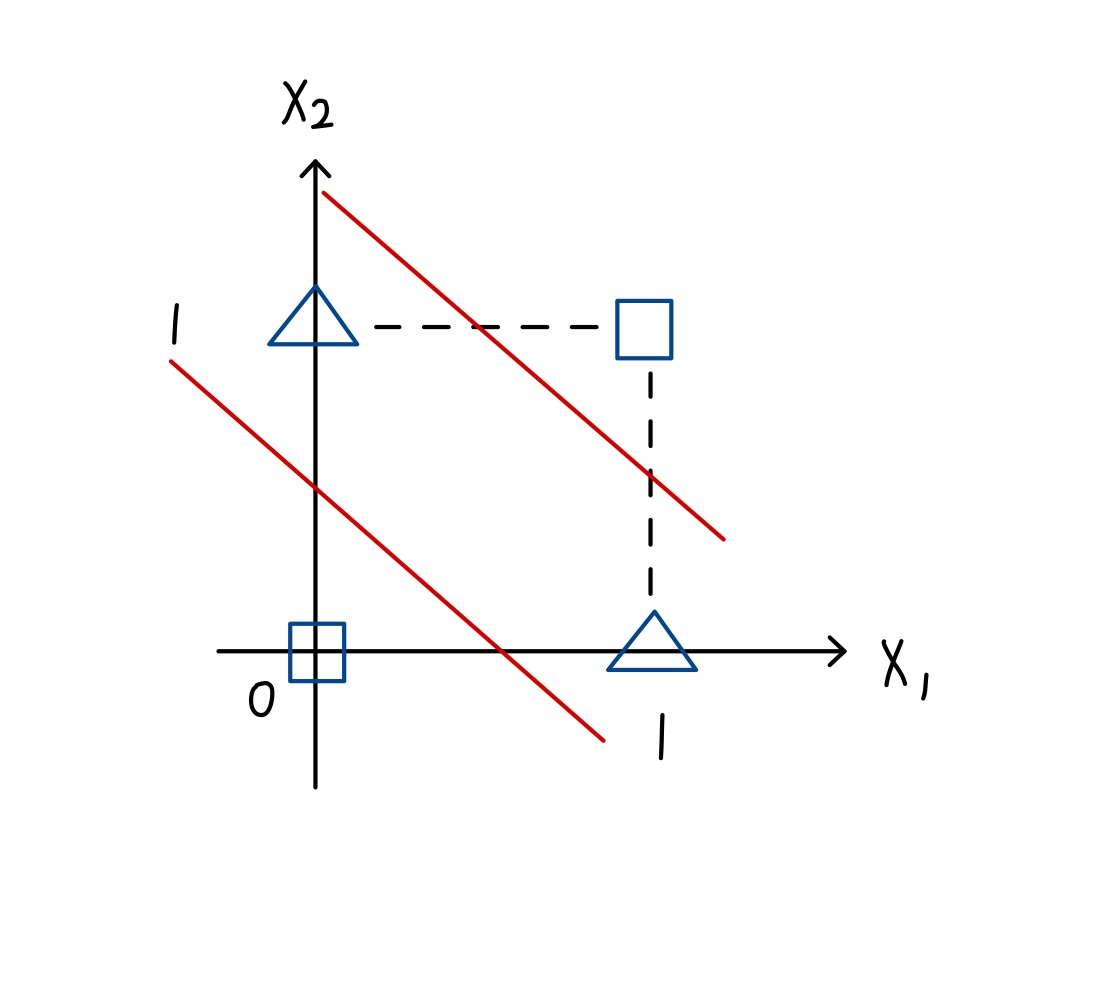
=> First winter of AI
2) MLP is the solution
🔸 MLP는 두 개의 직선(Decision boundary)으로 구분할 수 있어 위와 같은 경우 영역 구별할 수 있음
🔸 두 개의 layer로 구성. 각 layer마다 하나의 boundary를 만들 수 있어 nonlinear한 문제 해결 가능
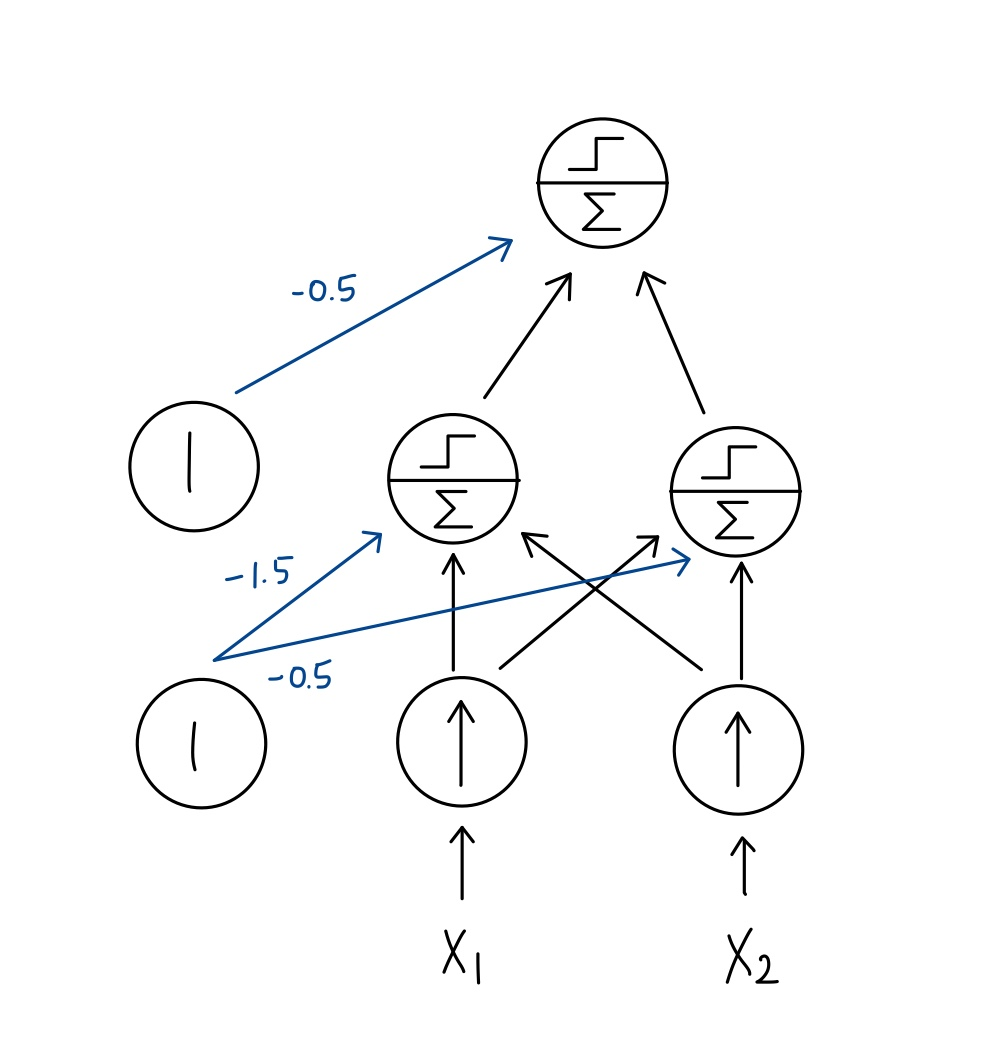
2. MLP
1) Input layer, hidden layers(LTUs), output layers(LTUs)
2) a bias neuron is fully connected to layers(hidden and input)
🔸 bias neuron은 input layer와 hidden layers에 존재. output layer에는 존재하지 않음
3) deep neural network(DNN): two or more hidden layers
🔸 2개 이상의 hidden layer를 deep neural network라 부름
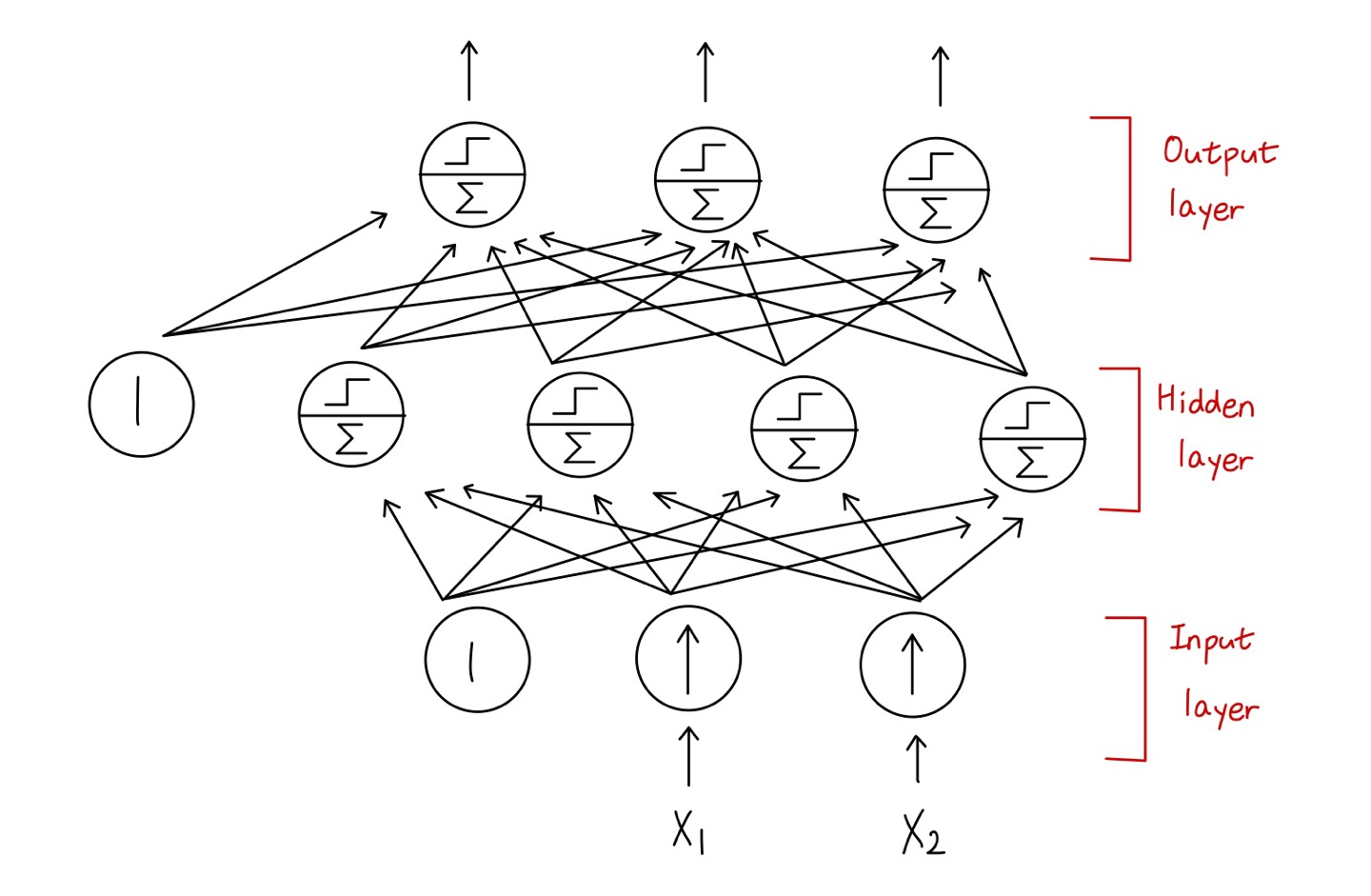
3. Backpropagation training algorithm(Rumelhart, 1986)
🔸 기존 single layer에서는 input layer와 output layer만 존재해 train시키기 쉬웠지만, 2개 이상의 hidden layer가 존재할 수록 조절해야하는 weight가 많아져 학습이 복잡해짐
ex. 위그림과 같은 perceptron에서는 input layer와 hidden layer 사이의 weight들, hidden layer와 output layer 사이의 weight들을 조절해야하므로 복잡도 증가
1) First successful training MLPs
🔸 첫번째 성공적인 MLP 학습 알고리즘 => Backpropagation training algorithm
2) Gradient Descent using automatic computing gradients in two passes
🔸 Backpropagation은 forward pass와 backward pass로 GD를 적용하는 방식. 이 때 automatic computing gradients 방식 사용.
🔹 automatic computing gradients은 forward pass 진행하면서 계산한 w 값을 저장(backward pass 때 사용하기 위해)
🔸 reverse-mode autodiff (Appendix D)
🔹 Tensorflow의 경우 reverse-mode autodiff를 이용해 automatic computing gradients 알고리즘 구현
🌟 기존의 perceptron은 nonlinear한 문제 해결 불가능하므로 Multi-layer로 perceptron을 구성해(MLP) nonlinear한 문제 해결. 이 때 MLP를 학습시키는 방법이 Backpropagation 알고리즘
📌 MLP training
🔸 Backpropagation이라는 MLP 학습법이 현재 deep learning 학습의 기반이 됨
1. Epoch: full training set processing
🔸 epoch이란 모든 training set에 대해 한 번의 processing을 진행하는 기본 단위
ex. training data에 100개의 data가 있을 경우 100개에 대해 전부 processing이 끝났을 때가 1 epoch
1) Multiple steps for each mini-batch
🔸 step이란 입력이 forward pass를 진행(입력->출력)한 후 backward pass(출력->입력)를 진행하는 하나의 과정
🔸 mini-batch는 여러개의 데이터를 한 번에 처리하는 것. 한 번에 처리한 mini-batch를 여러 번 진행하여 모든 데이터셋에 대해 한번씩 진행되면 하나의 epoch만큼 진행된 것
🔸 모든 데이터를 한 번에 처리하게 되면 한 번 processing한 것이 하나의 epoch이 됨 => Batch
💡 한 번에 몇 개의 데이터를 처리하든 상관없이 모든 training set에 대해 processing을 마치는 단위가 epoch
2. Backpropagation
1) Forward pass: feed forward all instances in a mini-batch intermediate results are stored for backward pass
🔸 mini-batch 안의 모든 instance들을 feed forward. output node까지 진행
🔸 모든 노드의 중간 결과는 backward pass를 위해 LTU에 저장. 큰 저장 공간 필요
🔸 Prediction: only final outputs are kept
train을 위한 backpropagation을 하지 않고 prediction만 할 경우 중간 값을 저장할 필요없고 final output만 필요
2) Measures network's output error (loss function)
🔸 loss function에 따라 error 계산
🔸 error 값은 loss function에 따라 달라짐
3) Computes how much each output connection contributed to the error
🔸 각 output connection이 최종 출력 error 값에 얼마나 기여했는지 계산
4) Measures how much of these error contributions came from each connection in the layer below
🔸 위에서 계산한 error값에 그 아래의 각각의 connection이 얼마나 기여했는지 계산
🔸 working backward until the input layer
🔹 input layer까지 이전의 connection이 얼마나 기여했는지 계산 반복
🔸 measures the error gradient across all the connection weights by propagating the error gradient backward
🔹 backward를 진행하면서 모든 connection weight에 대해 error gradient 계산
🔹 gradient가 큰 값을 가질수록 기여를 많이 함을 의미
5) Performs a Gradient Descent step to tweak all the connection weights in the network
🔸 Gradient Descent step을 수행하면서 gradient가 큰 weight에 대해 weight 값 조절
🔸 error gradient 값에 따라 얼마나 변화시킬지 결정
3. Backpropagation training algorithm
1) Forward pass: feed-forward instances in a mini-batch => prediction with intermediate results
🔸 mini-batch의 모든 instance를 output까지 feed-forward하며 그 중간값은 모두 저장
🔸 => prediction 진행
2) Reverse pass: measures the output error and error contribution (using error gradient) in reverse direction
🔸 output error 계산 후 input layer까지 error contribution 계산(error gradient 사용)
🔸 => error 계산해 contribution 탐색
3) Gradient Descent step: slightly twea ks the connection weights to reduce the error
🔸 Gradient Descent step 거침
🔸 error를 줄이기 위해 connection weight 값을 얼마나 변화시킬지 결정
🔸 => weight 값 바꿈
💡 가장 좋은 결과를 내는 weight값 찾는 과정이 MLP training 과정
4. Activation function
🔸 perceptron은 simple model과 달리 threshold를 위한 activation function을 LTU에 가짐
🔸 step function뿐만 아니라 다양한 함수를 activation function으로 사용할 수 있음
1) Step function (no gradient)
🔸 step function은 gradient 값을 구할 수 없음
🔸 derivates에서 0에서만 무한대에 가까운 값을 가지고 나머지는 0
🔸 gradient가 없다는 것은 학습을 할 수 없다는 것을 의미 (reverse pass에서 error gradient를 가지고 error contribution 계산)
🔸 step function은 backpropagation의 학습 방법에 적합하지 않음
🌟 따라서 logistic or sigmoid function 사용
🔹 activation: 0에서 1사이의 값 가짐
2) Other activation functions
🔸 hyperbolic tangent function
🔹 초기의 normalized한 값을 표현할 때 사용. sigmoid function 사용한 공식 사용
🔹 activation: -1에서 1 사이의 값 가짐
🔹 derivates: sigmoid function의 derivates 값을 키운 형태의 derivates 값 가짐
🔸 ReLU function
🔹 학습이 가장 잘 되어 가장 많이 사용되는 함수
🔹 activation:z가 0보다 작을 때는 0, 아닐 경우 linear
🔹 derivates: 0보다 작으면 0, 0보다 크면 1
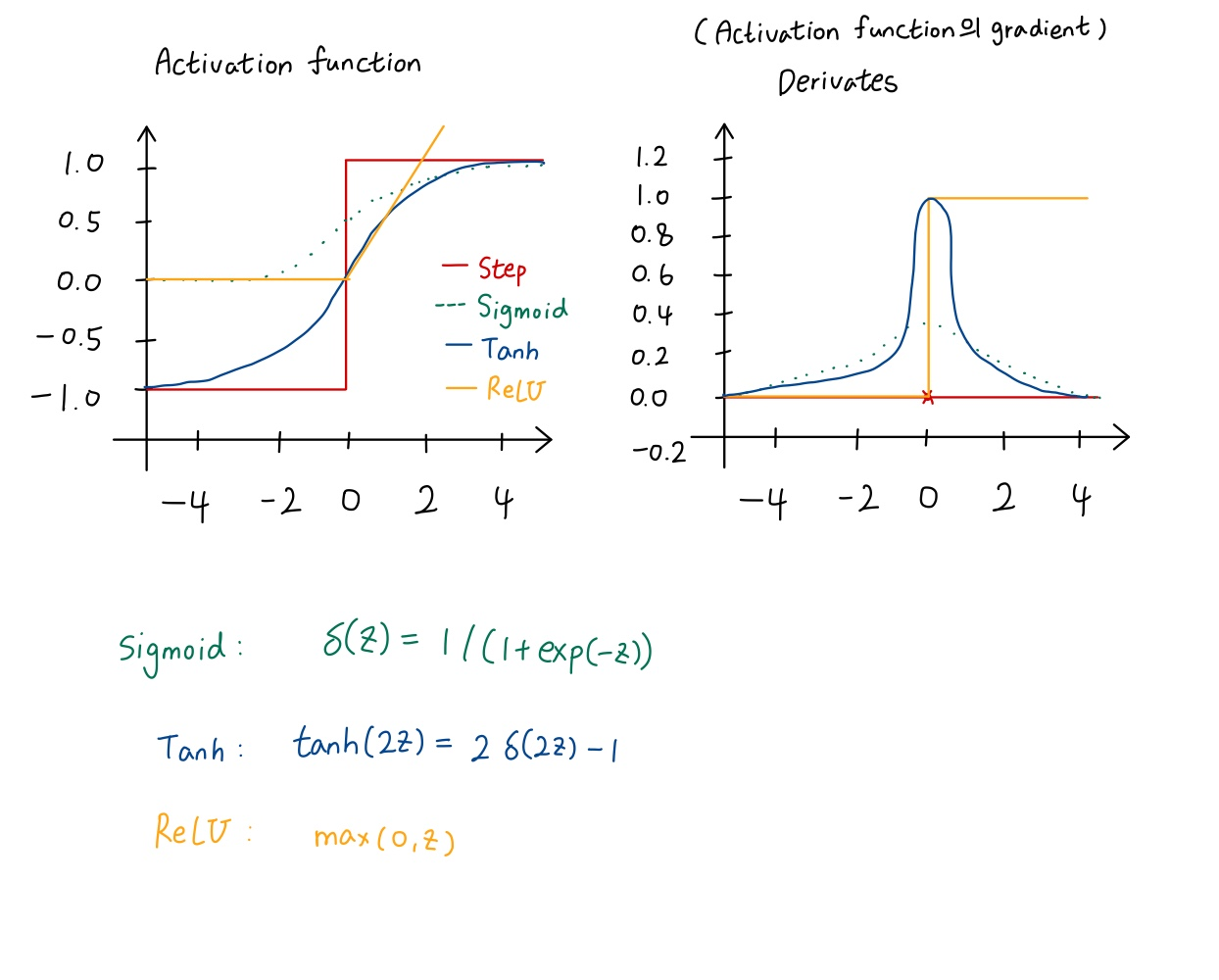
📌 Activation function and Weight initialization
🔸 LTU에서 activation function 사용
1. Why activation function?
🔸 인간의 신경세포가 activation 함수와 비슷하게 동작하기 때문
1) Chain several linear transformations => a linear transformation
🔸 여러 linear transformation의 chaining을 여러 번 진행해도 linear transformation => 동일한 복잡도
ex. f(x)=2x+3, g(x)=5x-1 => f(g(x))=2(5x-1)+3=10x+1
🔸 activation function이 없는 경우에는 perceptron layer(hidden layer)가 아무리 많아도 아무 의미 없다는 것 의미
🔸 activation function이 없으면 layer를 여러 개 쌓아도 single layer(hidden layer가 모두 사라지는 모양)와 같은 모양이 되어 MLP가 의미가 없어짐 => model의 complexity 증가하지 않음 => 복잡한 문제 해결 불가능
2) A layer with an activation function: nonlinearity is added to each layer any continuous function
🔸 각 layer에 activation function을 적용하면 각 layer마다 nonlinearity가 추가되므로 hidden layer가 많아질수록 복잡한 모델 생성 가능
🔸 hidden layer의 수가 complexity를 결정. layer가 많으면 복잡하고 적으면 단순
💡 activation function을 적용해야 hidden layer를 통해 복잡한 문제 해결 가능
3) A large enough DNN with nonlinear activations can theoretically approximate any continuous fuction
🔸 nonlinear activation을 가진 복잡한 DNN은 복잡한 모델을 continuous function으로 근사시켜 모델 생성해 문제 해결
🌟 activation function은 neuron network에 nonlinearity를 제공해 복잡한 문제를 해결할 수 있도록함
2. Weight initialization
🔸 Backpropagation을 이용한 학습 방법을 진행하면서 weight initialization(weight 초기화)을 생각해야함
1) Initialize all the hidden layers' connection weights randomly
🔸 Initialization을 통해 초기 weight 값을 정해주고 초기 값을 통해 최초의 forward pass 진행
🔸 weight 값은 random하게 정해지는데, 이는 weight 값이 서로 다르고 random하다는 것을 의미
2) With the same initial weights and biases,
🔸 All neurons in a given layer are perfectly identical => backpropagation affect them neurons remain identical => model will act as if it had only one neuron per layer
🔹 초기 weight 값과 bias 값이 모두 같을 경우, hidden layer에 있는 모든 neuron들이 모두 같은 값을 입력으로 받기 때문에 동일한 값 출력 => 각 layer에 여러 개의 neuron이 있지만 하나의 neuron을 가지고 있는 것과 동일하게 동작
📌 Neural Network
🔸 hidden layer가 1개인 경우 shallow network, 2개 이상인 경우 deep neuron network
1. Deep neural network
1) Good results of solving non-linear problem using multiple layers
🔸 multiple layer를 사용해 학습을 잘 시키면 더 복잡한 non-linear 문제를 해결하는데 좋음
🔸 하지만 복잡해질 수록 학습시키기 어려움
📌 Regression MLPs
🔸 regression과 classification 중 regression
1. Predict values
1) a single value: a single output neuron
🔸 입력에 대한 하나의 값 출력 => 출력 layer의 neuron이 하나
2) multivariate regression: multiple values, one output neuron per output dimension
🔸 N개의 값이 출력 => 출력 layer에 N개의 neuron 존재
🔸 ex. place a bounding box around the object: 2D center coordinates, width and height => four output neurons
🔹 object가 있고 그것을 감싸는 박스를 만들려면 center좌표(x,y), width,height 총 4개의 값을 주면 박스를 만들 수 있음 => output layer neuron 개수 4개
2. MLP for regression
1) no activation function for the output neurons => free to output any range of values
🔸 output neuron에는 activation function을 적용하지 않음 => 출력값이 변형되어 정확한 결과 값을 알아낼 수 없음
🔸 출력 값이 가능한 모든 범위의 값을 갖도록 함
2) Positive output: ReLU or softplus(z)=log(1+exp(z)) activation
🔸 출력값이 항상 positive이면 ReLU나 softplus=log(1+exp(z))를 activation function으로 사용할 수 있음
🔸 출력이 항상 양수이면(ex.길이, 높이) 음수를 배제하기 위해 위와 같은 함수를 activation 함수로 적용
3) range of values: logistic function or hyperbolic tangent, and then scale
🔸 정해진 범위의 값만 출력하면 logistic function이나 hyberbolic tangent를 activation function으로 적용하고 scaling 진행
ex. 0~5사이의 값을 항상 출력하면 logistic function을 적용해 0~1사이의 값이 출력되도록하고 5를 곱함
ex. -3에서 3 사이의 값이 나오면 hyperbolic tangent를 적용해 -1에서 1 사이의 값을 만들고 3을 곱함
3. Loss function
🔸 어떤 함수를 이용해 loss 값을 계산할 것인가
🔸 regression은 MSE나 MAE 주로 사용
1) MSE
🔸 2차값
2) MAE: with a lot of outliers
🔸 1차값
🔸 outlier가 많은 경우 MAE 사용
3) Huber loss: MSE + MAE
🔸 MSE와 MAE에 가중치를 주어 함께 사용
4. 설계 방식
| Hyperparameter | Typical value | 참고 |
|---|---|---|
| # input neurons | One per input feature | MNIST의 경우, 28x28 pixel 존재하므로 input neuron 총 784개 |
| # hidden layers | Depends on the problem, but typically 1 to 5 | 문제의 복잡도에 따라 달라지며, 많아질수록 학습이 힘들어지며 컴퓨터 연산 능력과 메모리가 좋아야함 |
| # neurons per hidden layer | Depends on the problem, but typically 10 to 100 | hidden layer 당 neuron이 많을수록 복잡해짐 |
| # output neurons | 1 per prediction dimension | |
| Hidden activation | ReLU (or SELU, see Chapter 11) | |
| Output activation | None, or ReLU/softplus (if positive outputs) or logistic/tanh(if bounded outputs) | regression은 output activation이 없는 것이 기본이지만, 출력값의 범위에 따라 사용 가능 |
| Loss function | MSE or MAE / Huber (if outliers) |
🔸 # of input neuron과 # of output neuron은 문제에 따라 자동으로 결정됨. 입력 instance의 vector dimension이 얼마인지에 따라 input neuron 결정되고, 출력에서 요구하는 값이 얼마냐에 따라 output neuron이 결정됨
🔸 따라서 hidden layer와 neurons per hidden layer를 결정하여 설계해야함
📌 Classification MLPs
🔸 regression과 classification 중 classification
1. Binary classification
🔸 positive인지 negative인지 판단
🔸 0이면 negative class, 1이면 positive class
1) a single output neuron using the logistic activation function
🔸 logistic activation function을 이용해 0~1 사이의 값 출력
2) output:[0,1]=>estimated probability of the positive class
🔸 threshold를 정하여 probability 알 수 있음
🔸 ex.threshold가 0.5일 때 0.5보다 작으면 0으로, 0.5보다 크면 1로 판정. 값이 0.8이 나오면 0.8이라는 확률로 1 출력. 이 결과는 0.6 이라는 값을 얻어 1로 출력한 결과보다 신뢰성 있음(error 발생할 가능성 적음)
2. Multilabel binary classification tasks
1) Ex.incoming email is ham or spam, and simultaneously urgent or nonurgent
🔸 ham인지 spam인지 판정하는 동시에 urgent한지 아닌지도 판정
2) two output neurons with logistic activation functions:
🔸 the probability of spam and urgent mail, respectively
🔸 하나의 output neuron은 ham인지 spam인지, 하나의 output neuron은 urgent인지 nonurgent인지
🔸 두 output neuron은 서로 독립적
🔸 (ham, urgent), (ham, nonurgent), (spam, urgent), (spam, nonurgent) 4가지 조합의 값 출력 가능
3. Multiclass classification with exclusive classes
🔸 exclusive classes: 여러 개의 class 중 하나의 class에만 속할 수 있음
ex. MNIST. 0~9까지의 숫자 중 하나의 숫자로 판정됨. 1이면서 3이라고 할 수 없음
1) One output neuron per class with softmax activation
🔸 class 당 하나의 output neuron을 가지며 softmax activation function 사용
🔸 softmax activation을 사용한다는 것은 exclusive class라는 것
🔸 softmax는 여러개의 output neuron으로부터 입력을 받아 처리해 output neuron으로 출력하므로, activation function이 각 뉴런마다 독립적으로 존재하지 않고 여러 개의 뉴런에 대해 통합적인 activation function으로 존재
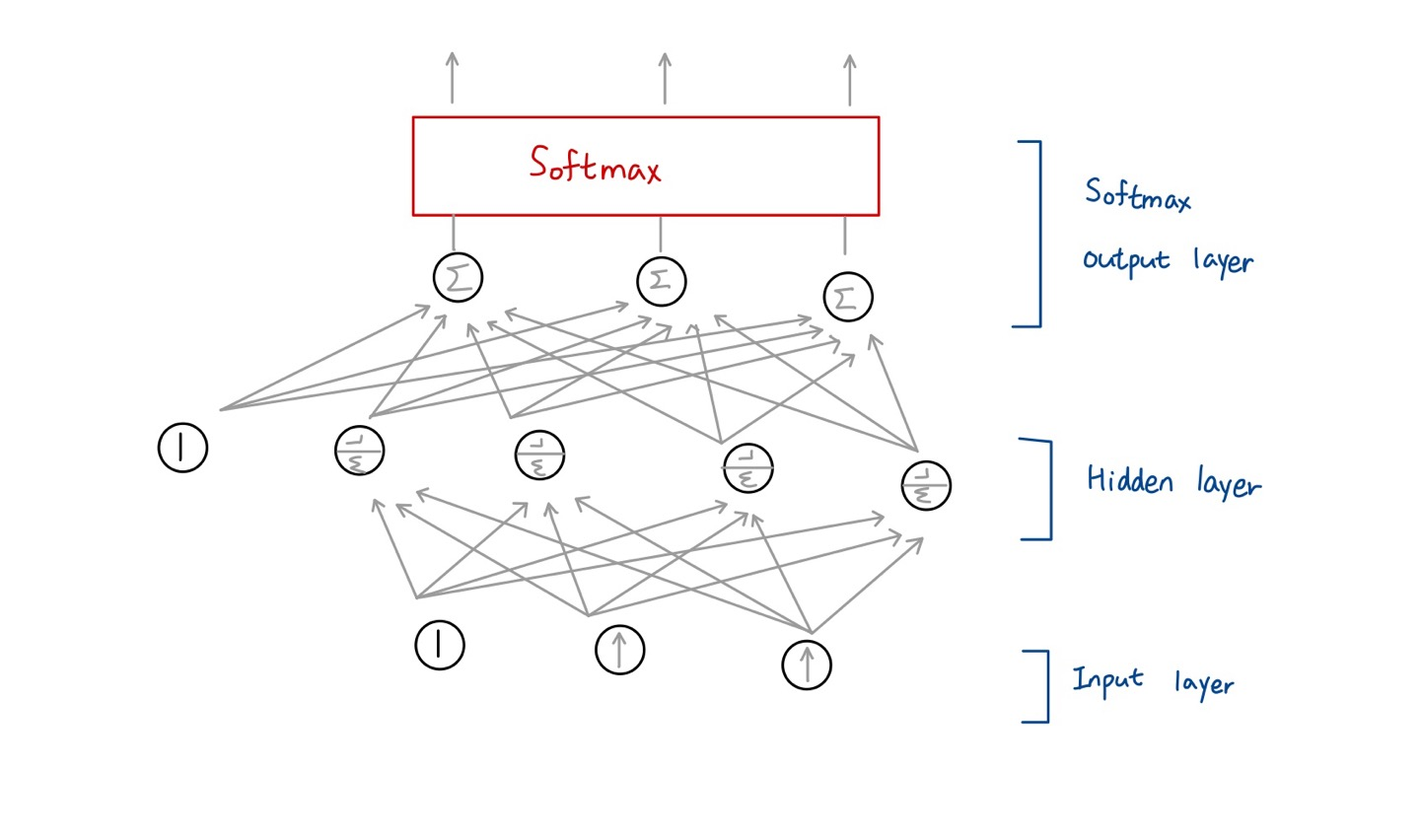
Softmax activation
각각의 출력은 0과 1 사이의 실수이고, 모든 출력의 합은 1로 확률로 볼 수 있음
4. Loss function: cross-entropy
5. 설계 방식
| Hyperparameter | Binary classification | Multilabel binary classification | Multiclass classification(exclusive) |
|---|---|---|---|
| Input and hidden layers | Same as regression | Same as regression | Same as regression |
| # output neurons | 1 | 1 per label | 1 per class |
| Ouput layer activation | Logistic | Logistic | Softmax |
| Loss function | Cross entropy | Cross entropy | Cross entropy |
