뷰 공간

카메라

• 게임이란 월드 공간을 시뮬레이션 하는 것이 아닌 플레이어를 대표하는 가상 공간의 아바타가 월드 공간을 탐험하는 형태로 구성되는 것이 일반거

• 이러한 탐험은 보통 아바타를 중심으로 일정 영역 내 위치한 시야 영역을 모니터 화면에 표시하는 형태로 구현되며 이는 월드 공간의 일부분을 화면에 표현하는 방식으로 구현

• 이렇게 월드 공간의 일부를 화면에 보여주기 위해 월드 공간을 재배치한 공간을 뷰 공간이라 함

  • 월드 공간만 있는 경우
    
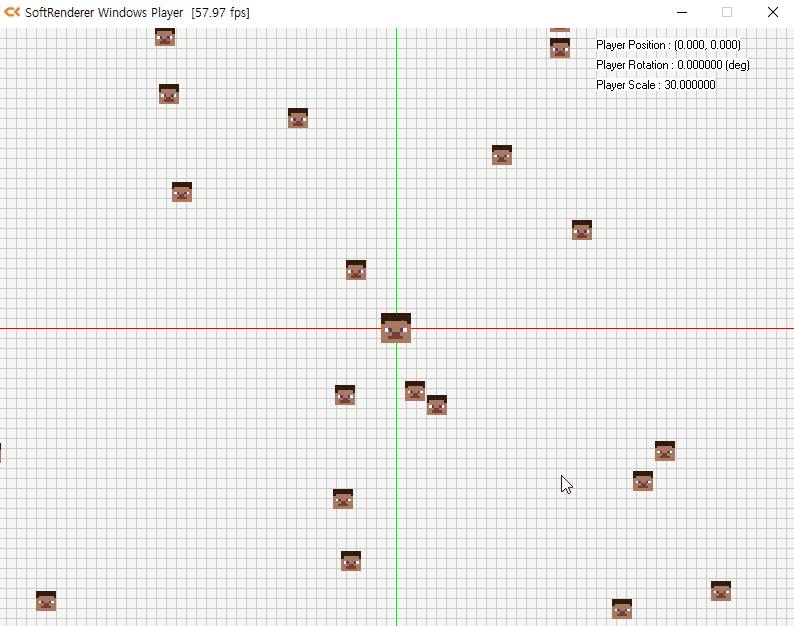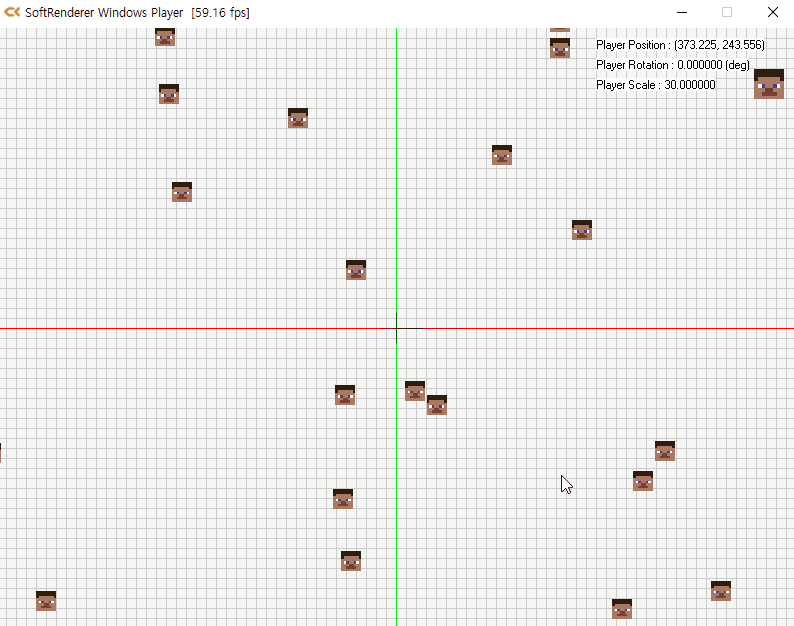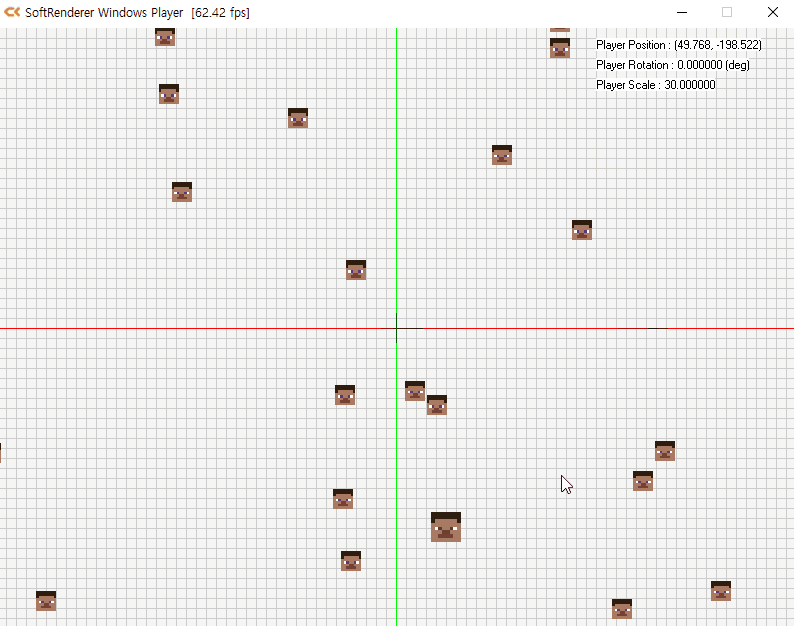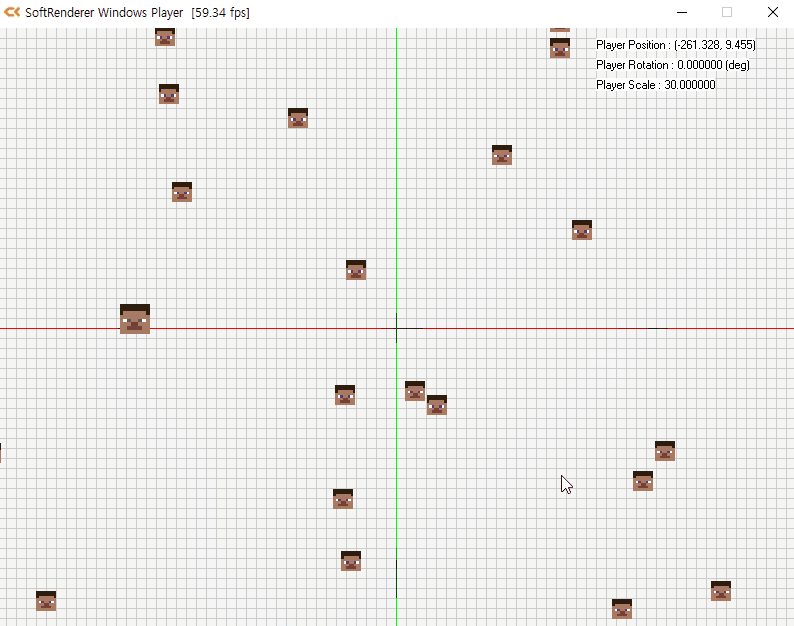
  • 뷰 공간을 추가한 경우
    

뷰 공간

• 카메라를 원점으로 월드 공간을 재배치한 공간을 의미
• 다음과 같이 카메라가 $(-10, -10)$에 있을 때 카메라를 원점으로 하는 물체의 위치는 $(20, 20)$이 됨

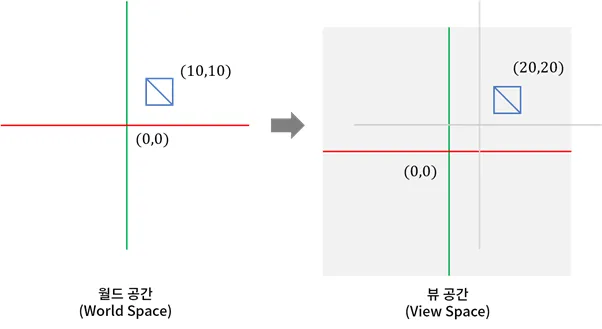
• 왜 $(20, 20)$이 되는지 메커니즘을 분석하면 다음과 같음

  • 기존 월드 공간을 기준으로 하는 카메라 위치를 역으로 계산한 값에 물체의 위치를 더하면 됨
  $(20,20)=-(-10,-10)+(10,10)$

  

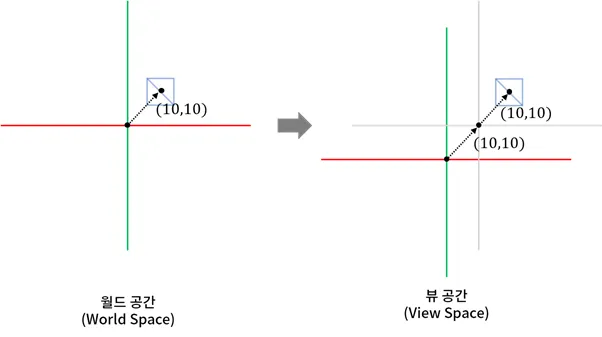
• 위의 식을 분석하면 위치에 대한 역은 이동 역행렬로 계산할 수 있으며 벡터의 덧셈은 이동 행렬의 곱셈으로 표현 가능

• 따라서 위 식은 다음과 같은 행렬로 표현이 가능

뷰 행렬의 계산

• 게임 오브젝트의 모델링 행렬은 다음과 같이 지정되며 메시 데이터의 한 점이 화면에 나타나기까지는 다음의 변환 과정을 거침

• 여기서 카메라 오브젝트가 주어진다면 카메라 오브젝트의 트랜스폼을 기반으로 월드의 점은 다음과 같이 변환 가능

0 위의 $T_c^{-1}$에 해당하는 행렬을 뷰 행렬이라고 하며 카메라의 트랜스폼 정보가 있으면 생성 가능

• 만일 카메라가 이동 외에도 회전 기능이 들어있다 가정

• 카메라의 회전하면 플레이어의 입장에서는 반대로 회전하는 것으로 보여짐

• 따라서 회전 기능이 들어가는 카메라는 다음과 같이 해석될 수 있으며 이는 트랜스폼에 역행렬을 취한 결과와 동일

• 하지만 카메라의 경우 스케일이 의미가 없으므로 다음의 수식으로 정리 가능

• 카메라 트랜스폼으로부터 회전까지 감안해 생성되는 뷰행렬은 다음과 같이 계산 가능

• 다음과 같은 로직으로 씬에 속한 최종 게임 오브젝트를 렌더링
  • 카메라로부터 뷰 행렬(V)을 구해 계산한다.
  • 씬에 속한 모든 게임 오브젝트를 순차적으로 순회한다.
    • 게임 오브젝트의 모델링 행렬(M)을 계산한다.
    • 뷰 행렬과 모델링 행렬을 곱한 결과를 최종 행렬로 저장한다. $T_{final}=V\cdot M$
    • 최종 행렬과 메시의 정점을 모두 곱한다. $v_{view}=T_{final}\cdot v_{local}$
    • 변환된 정점으로부터 삼각형을 생성하고 이들을 각각 칠한다.