게임 수학

수의 시각화 왜 수에 대해 알아야 하는가? 게엠 세계는 벡터로 구성한 탄탄한 시스템 이 시스템 위에서 콘텐츠를 완성 벡터는 수를 사용해 만들어진 대상이므로, 벡터를 정확히 이해하기 위해서는 결국 수가 만들어내는 시스템에 대해 이해가 필요 수 (Numbers)의 종류

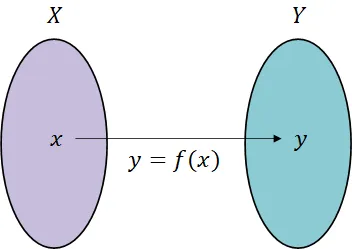
게임의 공간을 구성하고 화면에 보여지는 전 과정은 대부분 공간과 공간의 변환으로 구성이러한 변환은 근본적으로 집합과 집합의 대응 관계에 기반하고 있으며, 이의 메커니즘을 설명하는 이론이 함수함수의 성립 조건 : 첫번째 집합의 모든 요소가 사용되어야 함함수가 아닌 대응

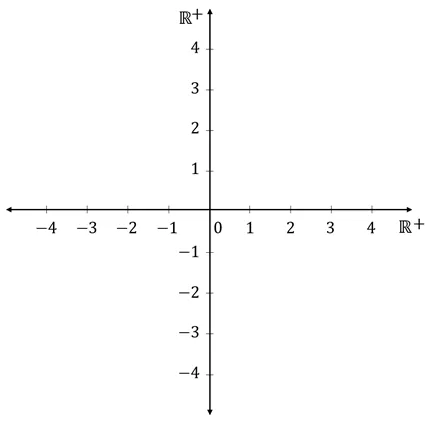
수를 점으로 표현한다면 1차원의 도형 수직선 위에 있는 것들만 표현이 가능1차원 상에서 의미있는 무언가를 표현하기에는 주어진 공간이 너무 부족수의 시스템을 기반으로 영역을 확장해 표현하는 방식두 실수 집합을 교차시켜서 평면을 표현하고 오른쪽과 위쪽을 + 방향으로 지정출

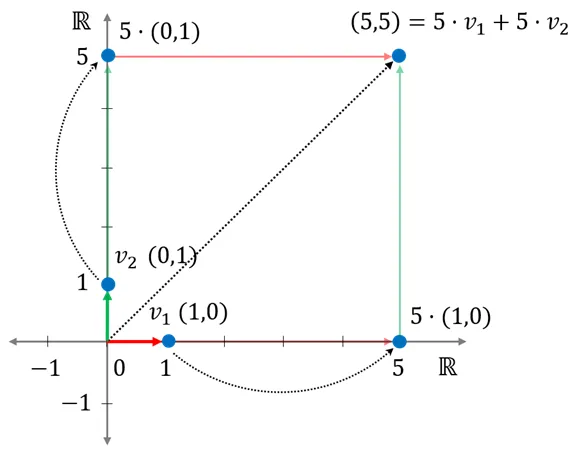
벡터의 기본 연산을 사용해 새로운 벡터를 생성하는 수식다음 수식을 만족하는 0이 아닌 계수가 존재하면 수식 내 벡터들은 선형 의존다음 수식을 만족하기 위해 어떤 계수 값이 0이라면 수식 내 벡터들은 선형 독립위 식은 다음과 같은 연립 방정식으로 정리할 수 있다.벡터 (

직각 삼각형을 구성하는 세 요소 중 두 요소에 대한 비의 값$sin=\\frac{Opposite}{Hypotenuse}$$cos=\\frac{Adjacent}{Hypotenuse}$$tan=\\frac{Opposite}{Adjacent}$삼각비를 집합의 관점에서 대응

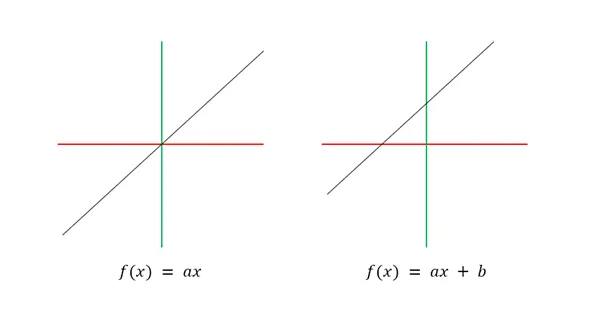
가산성 (Additivity) : $f(x+y)=f(x)+f(y)$1차 동차성 (Homogeneity of 1 degree): $af(x)=f(ax)$두 조건을 모두 만족할 때 선형성을 갖는다. $f(5+10)=f(5)+f(10) \\ 5f(10)=f(50)$$f(

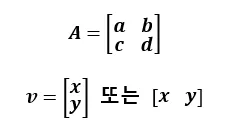
행렬 (Matrix)

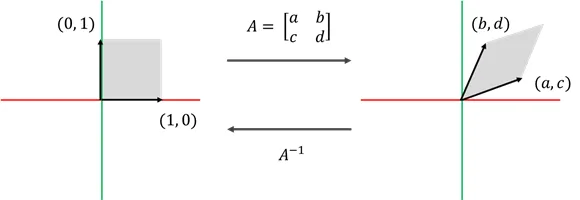
선형 변환의 결과가 변함없는 행렬두 표준 기저벡터 $e_1, e_2$의 값이 동일하게 유지되는 선형변환을 의미$$I=\\begin{bmatrix}1 & 0 \\ 0 & 1 \\end{bmatrix}$$$$\\begin{bmatrix}a & b\\c & d \\end{b

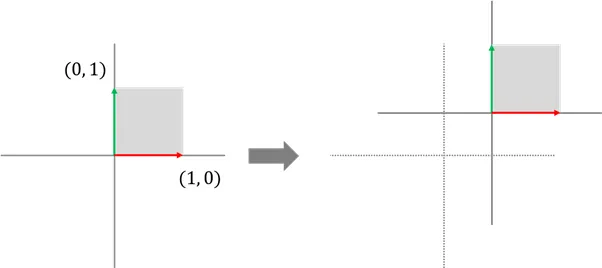
원점에서부터 시작하는 벡터의 특성상 기저벡터를 원점으로 부터 분리해 이동 불가즉 다음과 같은 행렬은 존재 x$$\\begin{bmatrix}a & b\\c& d \\end{bmatrix}\\begin{bmatrix}x \\y \\end{bmatrix}=\\begin{b

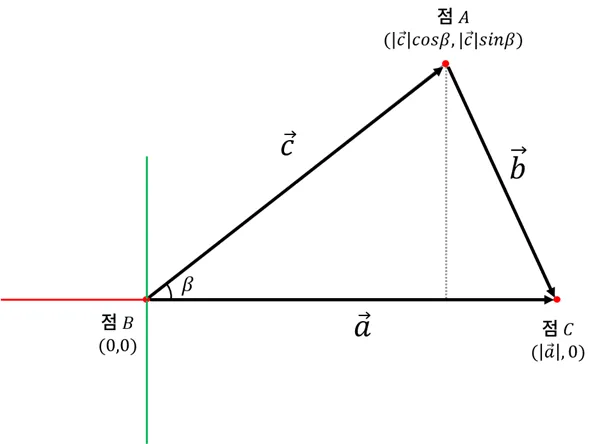
벡터의 연산기본 연산유용한 연산기본 연산이란?벡터 생성에 관여하는 중요한 연산유용한 연산의 종류벡터와 벡터의 곱 $(a, b, c) \\cdot (d, e, f) = (ad, be, cf)$벡터의 내적벡터의 외적 (3차원에서만 성립)$$(a, b) \\cdot (c,

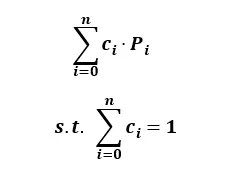
앞서서 아핀 공간에서 점 + 점의 연산은 불가능 하였음스칼라 보조를 사용하여 다음과 같은 조합식을 만들 때$$a\\cdot P_1 +b\\cdot P_2 = ?$$2차원의 점이라고 가정할 경우 위 조합식은 다음과 같이 전개됨$$a(x_1,y_1,1)+b(x_2,y_2,

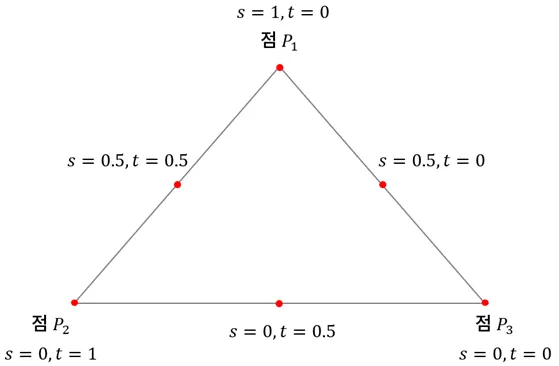
$$P'=s\\cdot P_1+t\\cdot P_2 +(1-s-t)\\cdot P_3$$세 점의 아핀 조합으로 만들 수 있는 공간의 형태는?$$P'-P_3=s(P_1-P_3)+t(P_2-P_3) \\\\vec{w}=s\\vec{u}+t\\vec{v}$$여기서 $\\ve

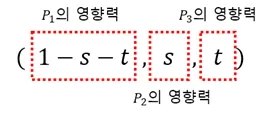
무게 중심좌표의 의미무게 중심 좌표는 선형적으로 보간됨따라서 무게중심좌표를 활용하면 삼각형의 내부를 칠할 때 선형적인 효과를 부여할 수 있음이를 위해 각 점에 위치와 더불어 부가적인 데이터를 부여이를 정점 (Vertex) 라고 함아래는 정점에 좌표와 더불어 색상 속성을

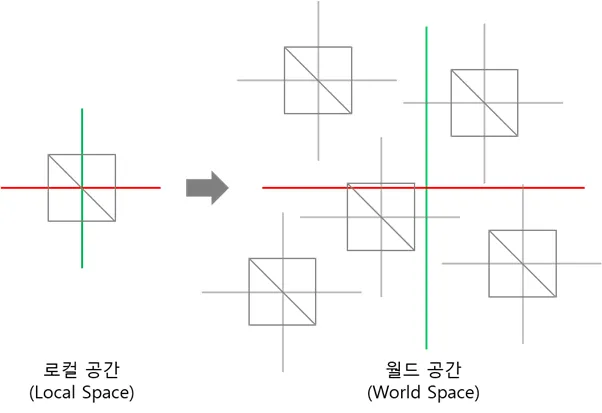
여러 점들이 모여 하나의 물체를 형성하는데 하나의 물체를 그리기 위해서는 원점 $(0, 0, 1)$을 중심으로 각점의 상대적인 위치를 지정해야 함이렇게 물체를 그리는데 사용하는 공간을 로컬 공간 (Local Space) 라고 함그런데 게임은 하나의 물체가 아닌 하나의

게임이란 월드 공간을 시뮬레이션 하는 것이 아닌 플레이어를 대표하는 가상 공간의 아바타가 월드 공간을 탐험하는 형태로 구성되는 것이 일반거이러한 탐험은 보통 아바타를 중심으로 일정 영역 내 위치한 시야 영역을 모니터 화면에 표시하는 형태로 구현되며 이는 월드 공간의 일