- 시점 (Viewing)
7.1. 시점 변환
7.2. 사영 변환
7.3. 원근 사영 (perspective projection)
7.4. 원근 변환의 특성
7.5. FOV (field of view)
7. 시점 (Viewing)
기하학적 변환의 중요한 용도 중 하나는 3차원 위치 (location)와 3차원 세계 상의 2차원 시점 위치 (position) 사이의 이동임. 이러한 3차원->2차원 매핑을 시점 변환 (viewing transformation)이라고 하며, 장면의 각 물체의 이미지 공간 위치를 빠르게 찾아야 하는 객체 순서 렌더링에서 중요한 역할을 함.
4. 레이트레이싱에서는 원근 뷰와 정사영 뷰의 여러 종류를 다루고 주어진 뷰에 따라 viewing ray를 생성하는 방법을 다뤘음. 이 챕터는 이러한 과정의 역에 관한 내용임. 행렬 변환을 사용하여 평행 또는 원근 뷰를 표현하는 방법을 다룰 것. 장면 (월드 공간) 상의 3차원 점을 이미지의 2차원 (이미지 공간) 점으로 사영하며, 주어진 픽셀의 viewing ray에 있는 점을 이미지 공간 상의 픽셀 위치로 사영함.
점을 월드에서 이미지로 사영하는 것은 와이어프레임 (wireframe) 렌더링을 생성할 때 좋음. 물체의 변에 대한 렌더링이 그려지고, 가까이 있는 표면은 멀리 있는 표면을 가리지 않음.
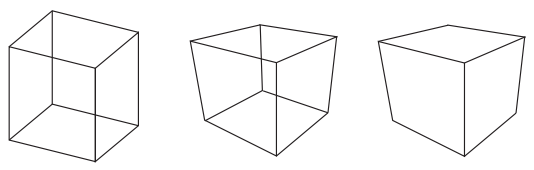
(왼쪽은 정사영으로 표현한 와이어프레임 큐브, 가운데는 원근 사영으로, 오른쪽은 보이지 않는 선들을 없앤 원근 사영)
레이트레이싱에서 각 viewing ray마다 가장 가까운 표면 교점을 찾아야 하는 것처럼, 실제와 비슷한 물체를 표시하기 위한 객체 순서 렌더링에서는 화면의 특정 지점에서 그려진 표면 중 가장 가까운 표면을 찾고 그 표면만 표시하면 됨.
이 장에서는 두 끝점을 갖는 좌표로 지정된 3차원 선분만으로 이루어진 모델을 그린다고 가정함.
7.1. 시점 변환
시점 변환은 표준 좌표계에서 좌표로 표현되는 3차원 위치 (location)를 픽셀 단위로 표현되는 이미지의 좌표로 매핑하는 작업임. 또한 이 작업은 카메라의 위치 (position)와 방향, 사영의 종류, 시야 (field of view), 이미지의 해상도 등 정말 많은 요소를 고려해야 하는 복잡한 작업임. 다른 복잡한 변환처럼 세부적이고 간단한 변환으로 세분화하여 접근하는 것이 좋음.
대부분의 그래픽스 시스템에서는 다음 세 단계 변환을 사용하여 이를 처리함.
- 카메라 변환 또는 눈 변환 (camera transformation or eye transformation): 카메라를 원점에 놓고 원하는 방향으로 변환하는 강체 변환 (rigid body transformation). 카메라의 위치 (position), 방향, 또는 포즈 (pose)에 의해 결정됨.
- 사영 변환 (projection transformation): 카메라 공간에서 점을 투영하여 볼 수 있는 모든 점들의 범위를 -1 ~ 1로 제한하는 변환. 사영의 종류에 의해 결정됨.
- 뷰포트 변환 또는 윈도잉 변환 (viewport transformation or windowing transformation): 단위 이미지 사각형을 픽셀 좌표에 맞는 사각형에 매핑함. 출력 이미지의 크기와 위치 (position)에 따라 결정됨.
이 단계를 쉽게 이해하기 위해 각 변환의 입출력에 해당하는 좌표계에 이름을 붙임.
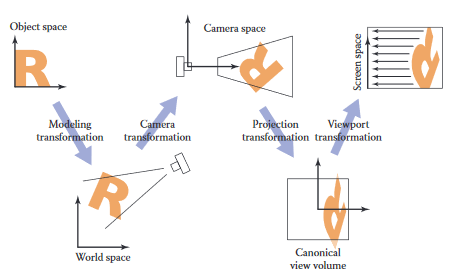
카메라 변환은 표준 좌표계의 점들을 카메라 좌표로 변환하거나 카메라 공간에 위치시킴.
사영 변환은 카메라 공간의 점들을 표준 뷰 볼륨 (canonical view volume)으로 이동시킴.
뷰포트 변환은 표준 뷰 볼륨을 스크린 공간에 매핑함.
7.1.1. 뷰포트 변환
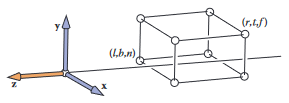
먼저 변환의 결과를 모든 조건에서 재사용할 수 있도록 해야 함. 먼저 보고자 하는 지오메트리가 표준 뷰 볼륨에 있다고 가정하고, 이를 정사영 카메라로 방향에서 보도록 할 것임.
표준 뷰 볼륨은 -1 ~ 1 사이에 있는 데카르트 좌표를 갖는 모든 3차원 점을 포함하는 큐브임, 즉
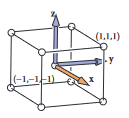
그런 다음 각각 을 화면의 왼쪽 면으로, 을 오른쪽, 을 아래쪽, 을 위쪽 면으로 투영함.
각 픽셀은 정수 좌표를 중심으로 하는 단위 사각형을 가지고 있음. 또한 이미지의 경계는 픽셀 중앙으로부터의 반-단위 오버슛을 가지며, 가장 작은 픽셀의 중앙 좌표는 임. 픽셀 이미지를 그린다면 사각형을 사각형에 매핑해야 함.
이제 모든 선분이 표준 뷰 볼륨 내부에 그려져야 한다고 가정할 수 있음.
뷰포트 변환이 축 정렬된 사각형을 다른 사각형에 매핑하기 때문에 이는 윈도잉 변환 중 하나임.
- (1)
사영 방향에 따른 점의 거리가 그 점이 이미지의 어느 위치에 사영되는지에 영향을 미치지 않기 때문에 위 행렬은 표준 뷰 볼륨의 점의 축 좌표를 무시할 수 있음. 하지만 이 행렬을 뷰포트 행렬이라고 부르기 전에 축 좌표를 변경하지 않고 이동할 수 있도록 행과 열을 추가해 주어야 함.
- (2)
7.1.2. 정사영 변환
물론 표준 뷰 볼륨 이외의 공간에 있는 지오메트리를 렌더링해야 하는 경우도 있음. 뷰를 일반화하기 위해 먼저 와 방향을 바라보도록 뷰의 방향 (direction, orientation)을 고정해야 하지만 임의의 사각형을 볼 수 있도록 해야 함. 뷰포트 행렬을 교체하기보다는 다른 행렬을 곱해서 크기를 늘림.
이러한 제한 속에서 뷰 볼륨은 축 정렬된 박스가 되며, 뷰 볼륨이 이 되도록 변의 좌표를 지정할 것임.
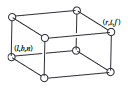
이러한 박스를 정사영 뷰 볼륨이라고 하며 다음과 같음 경계 평면을 참조함.
왼쪽 평면
오른쪽 평면
아래쪽 평면
위쪽 평면
가까운 평면
먼 평면
"왼쪽", "오른쪽"이라는 말은 축을 따라 고개를 방향으로 가리키면서 보고 있는 상황을 가정함. 이는 전체 정사영 뷰 볼륨이 음수 값을 가지면 이라는 "가까운" 평면이 인 경우에만 가깝다는 것을 의미함.
정사영 뷰 볼륨에서 표준 뷰 볼륨으로의 변환은 또다른 윈도잉 변환이므로 위 방정식을 사용하여 두 개의 뷰 볼륨을 빼서 다음 변환을 얻을 수 있음.
- (3)
정사영 뷰 볼륨에서 3차원 선분을 그리기 위해서는 선분을 스크린의 좌표에 사영하고 좌표는 무시함. 식 (2)와 (3)을 통해 이를 수행할 수 있음. 프로그램에서는 행렬들을 곱해서 새로운 행렬을 만들고 점을 조작함.
이제 좌표는 에 존재함. 지금 당장은 이렇게 한다고 해서 좋을 게 없지만, z-버퍼 알고리즘을 검사할 때 유용하게 사용할 수 있음.
끝점 를 갖는 3차원 선분을 그리는 코드는 다음과 같음.
M_vp를 구성한다
M_orth를 구성한다
M = M_vp * M_orth
for (a_i, b_i)의 각 선분마다 do
p = M * (a_i)
q = M * (b_i)
drawline(x_p, y_p, x_q, y_q)7.1.3. 카메라 변환
3차원의 뷰포인트를 변경하여 어떤 방향에서든 볼 수 있도록 해야 하는 경우가 있음. 바라보는 위치와 방향을 지정하기 위한 다음 여러 가지 방법 중 하나를 사용할 것임.
- 눈의 위치
- 시선의 방향
- 뷰업 (view-up) 벡터
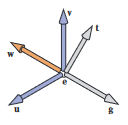
눈의 위치는 "어디에서 바라보는지"에 대한 것임. 그래픽스를 사진 기술로 생각한다면 눈의 위치는 렌즈의 중앙과 같음.
시선의 방향은 바라보는 방향이고, 뷰업 벡터는 바라보는 사람의 방향을 오른쪽과 왼쪽으로 이등분하고 땅에 서 있는 사람에 대해 하늘을 바라보게끔 가리키는 벡터임. 이러한 벡터는 원점 와 기저를 사용하는 좌표계를 설정할 때 좋음.
변환하고자 하는 모든 점이 원점 와 기저 벡터 를 갖는 좌표에 저장되면 됨.
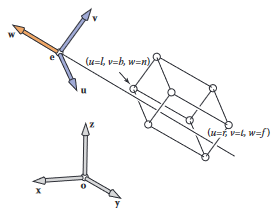
하지만 모델의 좌표는 표준 (월드) 원점 와 축에 저장됨. 전에 개발했던 시스템을 사용하기 위해서는 그려야 하는 선분 끝점의 좌표를 좌표에서 좌표로 변환해야 함. 이러한 변환이 이루어지도록 하는 행렬을 카메라 좌표 프레임의 표준-기저 행렬 (canonical-to-basis matrix)이라고 함.
- (4)
이는 점 를 원점으로 이동시킨 다음 를 로 정렬하는 것과 같은 변환임.
축만 사용하는 시점 알고리즘이 위치와 방향을 가리지 않는 카메라에서 작동하도록 하기 위해서는 카메라 변환을 뷰포트와 사영 변환의 곱에 추가하여 월드의 점들을 사영하기 전에 카메라 좌표로 변환해야 함.
M_vp를 구성한다
M_orth를 구성한다
M_cam을 구성한다
M = M_vp * M_orth * M_cam
for (a_i, b_i)의 각 선분마다 do
p = M * a_i
q = M * b_i
drawline(x_p, y_p, x_q, y_q)7.2. 사영 변환
뷰포인트는 원점에 위치하며 카메라는 축을 따라 바라봄.
원근법의 주요 특성은 화면 위에 있는 물체의 크기가 축의 음의 방향을 바라보는 원점에서의 눈의 에 비례한다는 것. 이는 다음 방정식으로 표현할 수 있음.
- (5)
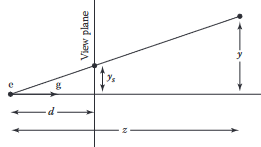
는 축을 따르는 점의 거리이고, 는 화면에 그려야 하는 점임.
원근 이미지를 그리기 위해서는 정사영을 위한 행렬을 사용해야 하고, 그런 다음에는 다른 행렬을 합성 행렬과 곱하고 기존 알고리즘을 사용할 수 있음. 하지만 입력 벡터 중 하나가 분모에 위치하는 변환의 경우 아핀 변환을 사용할 수 없음.
아핀 변환을 사용하기 위해 동차 좌표 (homogeneous coordinate)를 일반화한 나눗셈을 적용할 수 있음.
점 를 동차 벡터 로 표현할 수 있음. 이때 남은 좌표 는 항상 1이며, 를 아핀 변환 행렬의 네 번째 행으로 사용함.
변환을 구현할 때 행렬의 곱셈을 강제하기 위한 값으로 1을 사용하는 대신 좌표의 분모 (denominator)로 정의함. 동차 벡터 는 점 를 나타냄. 일 때와 다른 점은 없지만, 변환 행렬의 맨 밑의 행에 1보다 큰 모든 값이 올 수 있도록 하면 구현할 때 훨씬 넓은 범위의 변환을 사용할 수 있음.
구체적으로 보면, 선형 변환은 다음 식을 가짐.
또한 아핀 변환은 다음과 같음.
를 분모로 사용하면 가능성이 더욱 확장되어 함수를 다음과 같이 계산할 수 있음.
이를 의 "선형 유리함수"라고 함.
하지만 변환된 점의 모든 좌표에 대해 같은 분모를 가짐.
행렬 변환으로 표현하면 다음과 같음.
이러한 변환을 사영 변환 (projective transformation) 또는 호모그래피 (homography)라고 함.
