Overfitting
overfitting이란?
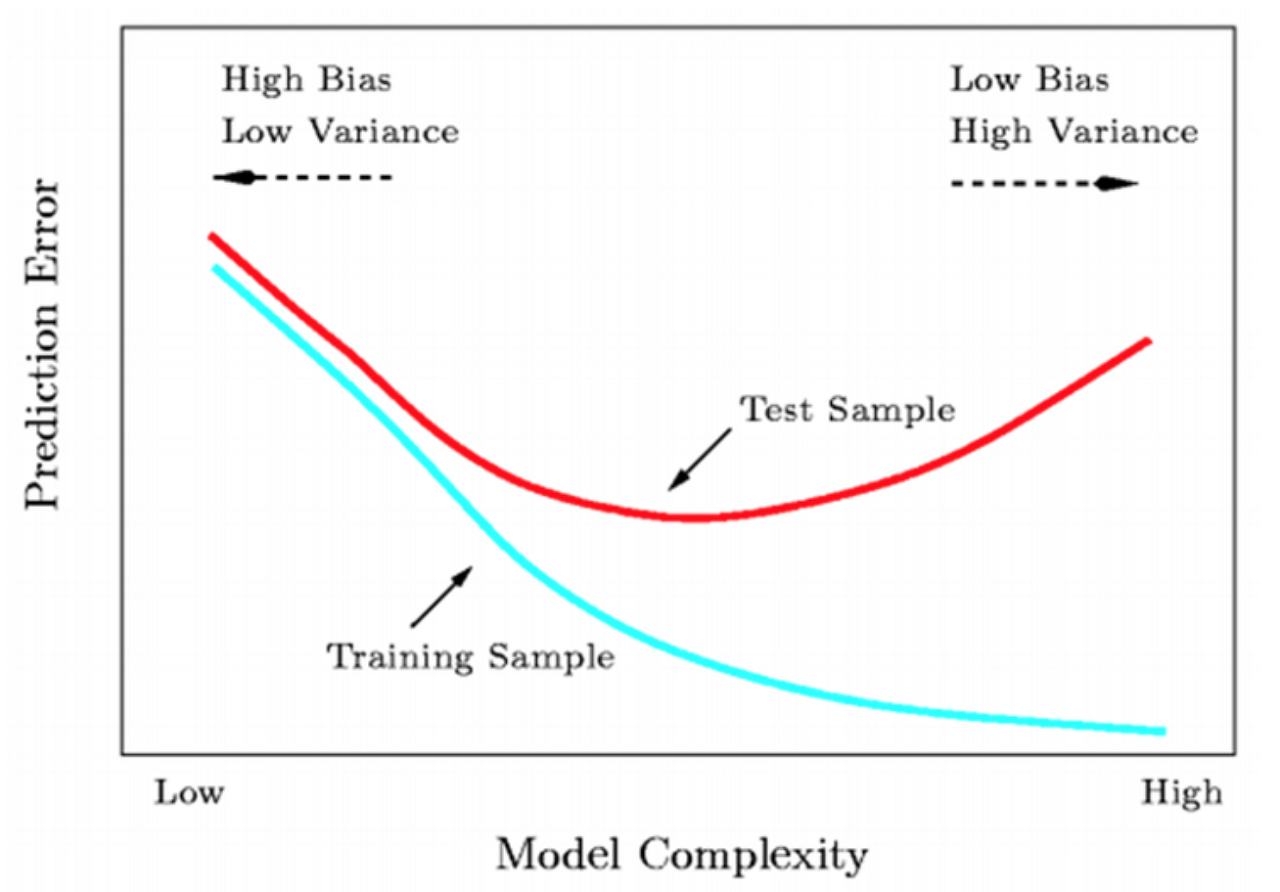
Overfitting은 학습 데이터(Training Set)에 대해 과하게 학습된 상황이다. 따라서 학습 데이터 이외의 데이터에 대해선 모델이 잘 동작하지 못한다. 학습 데이터가 부족하거나, 데이터의 특성에 비해 모델이 너무 복잡한 경우 발생한다. Training Set에 대한 loss는 계속 떨어지는데, Test Set에 대한 loss는 감소하다가 다시 증가합니다.
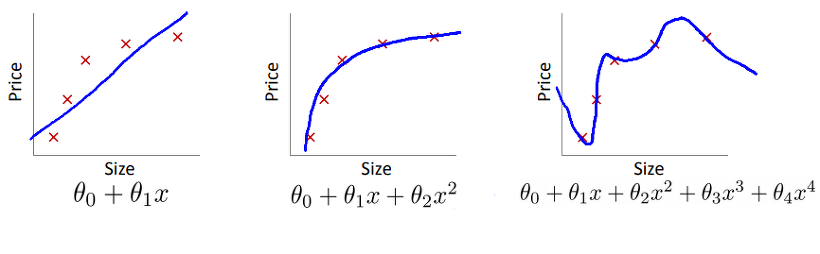
위와 같은 Linear Regression 집값 예측 문제가 있다고 할 때, 직선의 가설함수를 세울 때, 이차함수의 가설함수를 세울 때, 다차 함수의 가설함수를 세울 때 각각의 상황에 대한 판단이 아래와 같이 내려진다.
- 직선: Underfitting or high-bias
- 이차함수: Just Right
- 다차함수: Overfitting
또 다른 그림을 살펴보자.
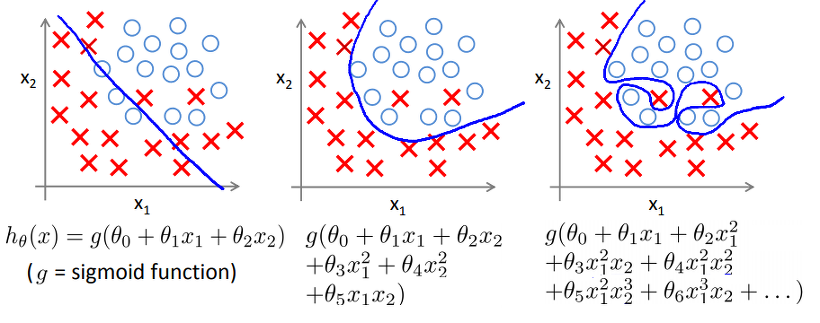
- 직선: Underfitting or High bias
- 이차식: Just Right
- 다차식: Overfitting or High variance
첫번째 직선의 경우는 직선과 데이터들이 잘 들어맞지 않는다. 두번째 포물선의 경우에는 우리가 얻을 수 있는 최적의 선으로 보인다. 마지막으로 엄청 고차원의 가설함수를 만들면 데이터에 딱 맞는 꼬여진 Decision Boundary를 갖게 되지만 제대로 된 예측을 해내지 못한다. 그리고 이를 Overfitting or High Variance 문제라고 한다. 그러면 어떻게 Overfitting인지 알 수 있을까?
1.가설함수의 그래프를 그려보거나, 2.학습데이터가 너무 적지 않은지 검사하는 방법이 있다.
또 이런 Overfitting 문제를 해결하기 위해서는 아래의 2가지 방법을 수행하면 된다.
- Reduce number of features
- L1/L2 정규화(L1/L2 regularization)
- 학습 데이터 늘리기(data augmentation)
Reduce number of features
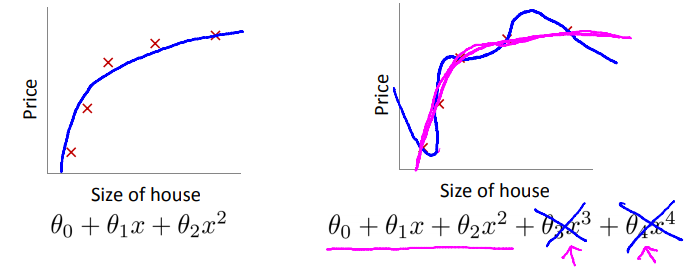
먼저 Feature들 중에서도 중복이 되거나 예측을 하는데 중요한 요소가 아닌 Feature들이 있을 수 있다. 그러므로 불필요한 Feature들을 먼저 제거해주거나 알고리즘이 어떤 특성을 사용할 것인지 자동으로 선택해주는 Model Selection Algorithm을 이용할 수도 있다. 그리고나서 Regularization(정규화)를 해주면 되는데, 정규화는 모든 특성을 유지하되 θ 에 미치는 영향규모를 줄이는 것으로 y를 예측하기 위한 수많은 Feature들이 존재하며 그 Feature들이 y에 영향을 주는 경우에 잘 작동한다. 즉, Regularization은 모델이 너무 복잡해지지 않도록 임의로 제약을 가하는 것이다.
L1/L2 정규화(L1/L2 regularization)
학습을 진행할 때, 학습 데이터에 따라 특정 weight의 값이 커지게 될 수있다.
이렇게 되면 과적합이 일어날 가능성이 아주 높은데,
이를 방지하기 위해 L1, L2 regularization를 사용한다.
1) l1 regularization
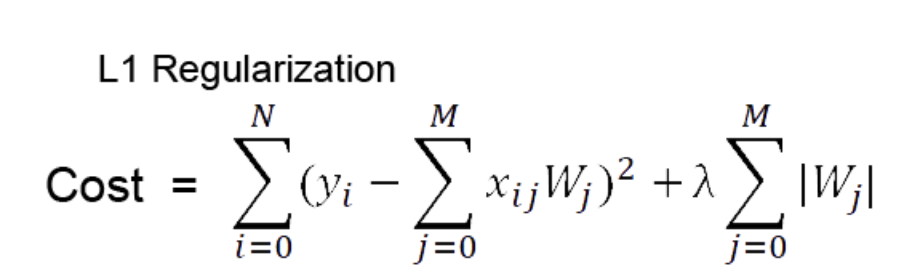
더하기 전 좌측이 일반적인 cost function이고 여기에 가중치 절대값을 더해준다.
편미분 을 하면 w값은 상수값이 되어버리고, 그 부호에 따라 +-가 결정된다.
가중치가 너무 작은 경우는 상수 값에 의해서 weight가 0이 되어버린다.
==> 결과적으로 몇몇 중요한 가중치 들만 남게된다
2) l2 regularization
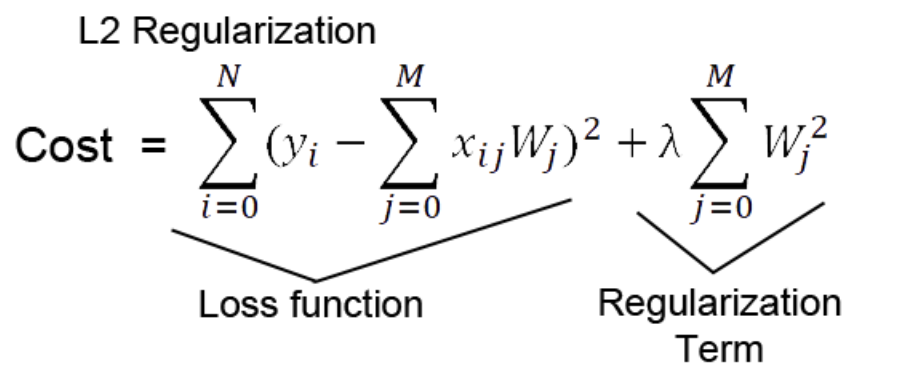
Cost function에 제곱한 가중치 값을 더해줌으로써 편미분 을 통해 back propacation 할 때, Cost 뿐만 아니라 가중치 또한 줄어드는 방식으로 학습을 한다.
특정 가중치가 비이상적으로 커지는 상황을 방지하고, Weight decay 가능해진다.
즉, 전체적으로 가중치를 작아지게 하여 과적합을 방지하는 것이다.
학습 데이터 늘리기(data augmentation)
모델은 데이터의 양이 적을 경우, 해당 데이터의 특정 패턴이나 노이즈까지 쉽게 암기하기 되므로 과적합 현상이 발생할 확률이 늘어난다. 그렇기 때문에 데이터의 양을 늘릴 수록 모델은 데이터의 일반적인 패턴을 학습하여 과적합을 방지할 수 있다.
만약, 데이터의 양이 적을 경우에는 의도적으로 기존의 데이터를 조금씩 변형하고 추가하여 데이터의 양을 늘리기도 하는데 이를 데이터 증식 또는 증강(Data Augmentation)이라고 한다. 이미지의 경우에는 데이터 증식이 많이 사용되는데 이미지를 돌리거나 노이즈를 추가하고, 일부분을 수정하는 등으로 데이터를 증식시킨다. 텍스트 데이터의 경우에는 데이터를 증강하는 방법으로 번역 후 재번역을 통해 새로운 데이터를 만들어내는 역번역(Back Translation) 등의 방법이 있다.
