MST(최소 신장 트리) - 프림 알고리즘

Spanning Tree(신장 트리)

Spanning Tree란 그래프 내의 모든 정점(노드)을 포함하는 트리를 의미한다.

Spanning Tree는 그래프의 최소 연결 부분 그래프이다.

예시) 노드가 n개라면 간선은 n-1개 입니다.

아래 두 예시는 Spanning tree 성립

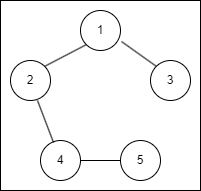
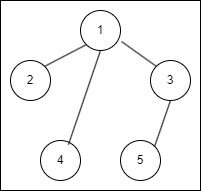
아래 예시는 Spanning tree 성립 x (5번 노드 포함 안함)

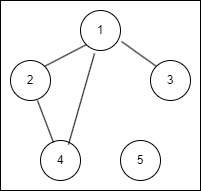
아래 예시도 Spanning Tree 성립 x (간선 개수 >= 노드 개수)

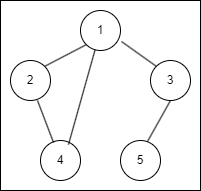
Spanning Tree의 특징은
1. DFS, BFS를 이용해서 모든 노드를 탐색 가능하다.
2. 하나의 그래프에는 다양한 신장 트리를 포함한다.

---

MST(Minimim Spanning Tree)

Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리

단순히 가중치가 가장 낮은 간선을 n-1개 사용한다고 최소 비용이 얻어지는 것은 아닙니다.

MST를 구할 수 있는 알고리즘은 크루스칼 알고리즘과 프림 알고리즘이 있다.

---

Prim 알고리즘

시작 정점에서부터 출발하여 신장트리를 단계적으로 확장 해나가는 알고리즘

정점 선택을 기반으로 하는 알고리즘이다.

1. 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
2. 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
   즉, 가장 낮은 가중치를 먼저 선택한다.

   이때 가중치가 가장 낮은 간선이라도 해당 간선에 의해 사이클이 형성되면 해당 간선을 추가하지 않고 넘어갑니다.

3. 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.

---

Prim 알고리즘 예시

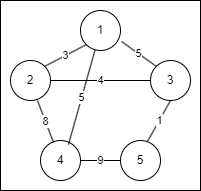
1. 1번 노드에서 시작
2. {1}번 노드에서 가장 가중치가 낮은 1-2 간선을 추가, 가중치 +3 (현재 노드: 1,2 , 가중치: 3)
3. {1,2}번 노드에서 가장 가중치가 낮은 2-3 간선을 추가, 가중치 +4 (현재 노드: 1,2,3 , 가중치: 7)
4. {1,2,3}번 노드에서 가장 가중치가 낮은 3-5 간선을 추가, 가중치 +1 (현재 노드: 1,2,3,5 , 가중치: 8)
5. {1,2,3,5}번 노드에서 가장 가중치가 낮은 간선은 1-3 간선, but 1,3은 이미 추가되있으므로(사이클 생성됨) 추가x
6. {1,2,3,5}번 노드에서 가장 가중치가 낮은 1-4 간선을 추가, 가중치 +5 (현재 노드: 1,2,3,4,5 , 가중치: 13)

---

실제 코드와 시간복잡도

가중치가 낮은 간선을 찾기 위하여 우선순위 큐를 사용하여 간선의 가중치를 오름차순으로 저장한다.

방문한 노드를 check 하기 위하여 visited 배열을 사용한다.

시간복잡도: $O(VlgE)$

노드 한개씩 탐색하는데, 탐색할때 마다 우선순위 큐에서 가중치가 가장 낮은 간선을 찾기때문에
V (노드개수) * lgE (우선순위 큐에서 간선 1개 시간복잡도)

---

c++ 코드 예시

vector<vector<pair<int,int>>> node; // 행: 노드번호, 열: {가중치, 가리키는 노드 번호} 

int prim(int num) { // num = 시작노드 번호

    pririty_queue<pair<int,int>, vector<pair<int, int>>, greater<pair<int,int>>> prim_pq;
	// {가중치 ,가리키는 노드 번호} 저장, 가중치의 오름차순으로 저장된다
    
    vector<bool> visited(그래프 노드 개수, false);
    
	visited[num] = true;
	int len = node[num].size();
	for (int i = 0; i < len; i++) {
		prim_pq.push(node[num][i]);
	}

	while (!prim_pq.empty()) {
		pair<int,int> cur = prim_pq.top();
		prim_pq.pop();

		if (visited[cur.first] == true) continue;
		
		visited[cur.first] = true;
		
		// 사이클이 생성안되고, 가중치가 낮은 간선을 찾은 상태
		// 다른 로직으로 변경가능
		
		result += cur.second;

		len = node[cur.first].size();
		for (int i = 0; i < len; i++) {
			pair<int,int> next = node[cur.first][i];
			if (visited[next.first] == true) continue;
			prim_pq.push(next);
		}
		
	}
    
    return result; // 모든 엣지 합 반환, 다른 로직으로 변경가능
}

크루스칼 알고리즘은 다음에...

저 나름대로 공부한 내용을 정리한 글입니다.
지적, 피드백 환영합니다.