Union-Find 알고리즘은 집합의 분할을 서로소인 부분 집합(분리 집합)으로 유지하는 데 사용되는 알고리즘이다.
이 알고리즘은 그래프에서 연결된 컴포넌트를 찾거나 그래프에서 사이클을 검출하는 등의 연결과 관련된 문제를 해결하는 데 특히 유용하다
크루스칼 알고리즘을 알기 위해 추가로 공부하게 되었다...
Disjoin Set (분리 집합)
분리집합이란 교집합이 존재하지 않는 두개 이상의 집합을 뜻한다.
{1,2,3}, {4} 두 집합은 분리집합
{1,2}, {2,3,4} 두 집합은 분리집합이 아니다 (2가 겹침)
Union-Find 알고리즘의 두가지 메서드
-
find(x) // x는 노드의 번호
x가 속한 집합의 대표값(루트노드)을 반환
x가 어떤 집합에 속해있는지 찾는 연산
-
union(x, y) // x, y는 노드의 번호
합집합 연산
x가 속한 집합과 y가 속한 집합을 합친다.
두 원소가 같은 집합인지 체크하고 싶다면,
find(x) == find(y)// 같은 집합에 속한다면 같은 루트 노드를 반환한다.
Union-Find 실제 코드
실제 코드에서, Union-Find 알고리즘을 트리로 구현한다.
자식노드가 부모노드를 가리키게 되어 있다.
int parent[MAX_NODE];
// 인덱스 번호가 자식노드의 번호, 배열의 값은 해당 노드의 부모노드를 의미함
parent[0] = 0; // 루트노드 (인덱스 번호와 해당 값이 같음)
parent[1] = 0; // 부모노드가 0
parent[2] = 0; // 부모노드가 0
parent[3] = 3; // 루트노드 (인덱스 번호와 해당 값이 같음)
// 여기서 {0,1,2}와 {3}은 분리집합find 메서드와 union 메서드
// 맨처음 parent 배열의 값들은 자기 자신의 번호로 초기화 되어있음
int parent[MAX_NODE];
int find(int x) {
if (x == parent[x]) { // x가 루트노드라면 그대로 반환
return x;
} else {
return find(parent[x]); // 루트노드를 찾아서 반환
}
}
void union(int x, int y){
x = find(x);
y = find(y);
// 두 노드의 루트노드를 받는다.
parent[y] = x;
// y의 부모노드를 x로 초기화
// -> y는 루트노드였지만, x의 자식노드가 된다
// -> y가 속한 트리가 x가 루트노드인 하위트리가 된다.
// -> x가 속한 집합과 y가 속한 집합이 같은 집합으로 뭉치게 된다.
}
각 메서드의 시간복잡도
find(x) -
해당 노드가 속합 집합(트리)의 대표값(루트노드)를 반환하는 메서드
최대 트리의 높이만큼 걸린다.
union(x, y) -
find(x) 메서드를 2번 사용하기 때문
추가적인 Union-Find 알고리즘 최적화
분리집합은 두 집합사이의 관계에만 의미가 있다.
두 집합이 분리집합인지 아닌지
한 집합 내에서, 원소들끼리의 관계는 의미가 없다.
-> 이를 이용해서 트리의 높이를 낮춰서 시간복잡도를 줄일 수 있다.
이러한 과정을 경로 압축이라고 합니다.
1 - Find 메서드 최적화
Find 메서드를 실행할때 특정 원소의 부모노드를 루트노드로 바꿔주면서 트리의 높이를 낮춰줄 수 있다.
int find(int x) {
if (x == parent[x]) {
return x;
} else {
return parent[x] = find(parent[x]);
// x의 부모노드를 루트노드로 변환
// -> x가 리프노드라면 해당 트리의 높이가 낮아질 수 있다
// -> 다음 Find 메서드를 호출할때 시간복잡도가 감소한다.
}
}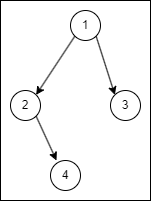
위 구조에서 find(4)를 호출한다면,
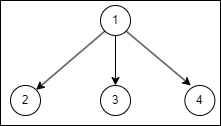
위 그림처럼 4의 부모가 1이 된다.
트리의 높이가 2에서 1이 되면서 find와 union 메서드의 시간복잡도가 줄어듭니다.
이렇게 할 수 있는 이유는, 트리 내에서 노드 사이의 관계가 없기 때문입니다.
트리는 그저 같은 집합임을 표현하는 구조입니다.
2 - Union 메서드 최적화
Union 메서드를 실행할때, 마지막에서, 높이가 더 낮은 트리를 높은 트리
-> 항상 높이가 더 낮은 트리를, 더 높은 트리 밑에 넣는다
-> 전체 트리의 높이가 낮아져서 시간복잡도를 줄일 수 있음
// nodeCount는 해당 노드가 속한 트리의 높이를 저장한 배열, 초깃값은 0
void Union(int x, int y) {
int rx = Find(x);
int ry = Find(y);
if (nodeCount[rx] < nodeCount[ry]) {
parent[rx] = ry;
}
else {
parent[ry] = rx;
if (nodeCount[rx] == nodeCount[ry])
nodeCount[rx]++;
}
}union 메서드를 최적화하는건 트레이드오프가 있습니다.
트리의 높이를 낮춰서 시간복잡도를 줄이지만, 각각의 노드마다 트리의 높이를 저장하는 배열을 추가적으로 선언해줘야 하기때문에, 공간복잡도가 조금 증가하게 됩니다.
그래서 굳이 각 노드가 해당하는 트리의 사이즈를 저장하지 않고, 작은 노드를 기준으로 합치기도 합니다.
void Union(int x, int y) { int rx = Find(x); int ry = Find(y); // 번호가 낮은 노드를 루트로 만든다. // 일관되게 트리를 합쳐서 약간의 경로 압축이 이루어진다. if(rx > ry) parent[rx] = ry; else parent[ry] = rx; }위 코드가 간단해서 위 코드를 자주 씁니다.
추가적인 경로 압축이 필요하다면 각 노드마다 트리의 사이즈를 저장해서 시간복잡도를 줄입니다.
최종 코드
vector<int> parent; // 초깃값 해당 인덱스 값 ( ex) parent[1]=1, parent[3]=3 )
vector<int> nodeCount; // 초깃값 0 ( ex) parent[1]=0, parent[3]=0 )
int Find(int x) { // 해당 노드의 루트노드를 반환하는 메서드
if (x == parent[x])
return x;
else return parent[x] = Find(parent[x]);
}
void Union(int x, int y) { // 두 노드가 속한 트리를 합하는 과정 (합집합)
int rx = Find(x);
int ry = Find(y);
if(rx > ry) parent[rx] = ry;
else parent[ry] = rx;
}