dfs와 bfs
dfs와 bfs는 여러가지 방법으로 구현될 수 있습니다. 예를 들면, 인접행렬과 인접리스트를 사용하는 것으로 나눌 수 있고, dfs에서는 스택자료구조르 만들어 사용하는 것과 재귀함수를 이용하는 방법으로 구현하는 방식으로도 나뉠 수 있습니다. 그래프 탐색을 처음 공부할 때, 내가 모르는 형태의 구현방법으로 적힌 다른 사람들의 풀이를 보고 어려움을 느낀 점이 많아 포스팅으로 남겨봅니다.
이 글에서는 각각의 방법을 직접 구현해보고, 장점과 단점에 대해서 이야기해보겠습니다. 이 글을 작성하기 위해서 백준 1260 dfs와 bfs 문제를 활용하겠습니다.
인접리스트와 인접행렬
인접리스트와 인접행렬은 그래프를 코드 상에서 표현하는 방식입니다. 아래의 그림으로 나타내어지는 그래프를 살펴보겠습니다.
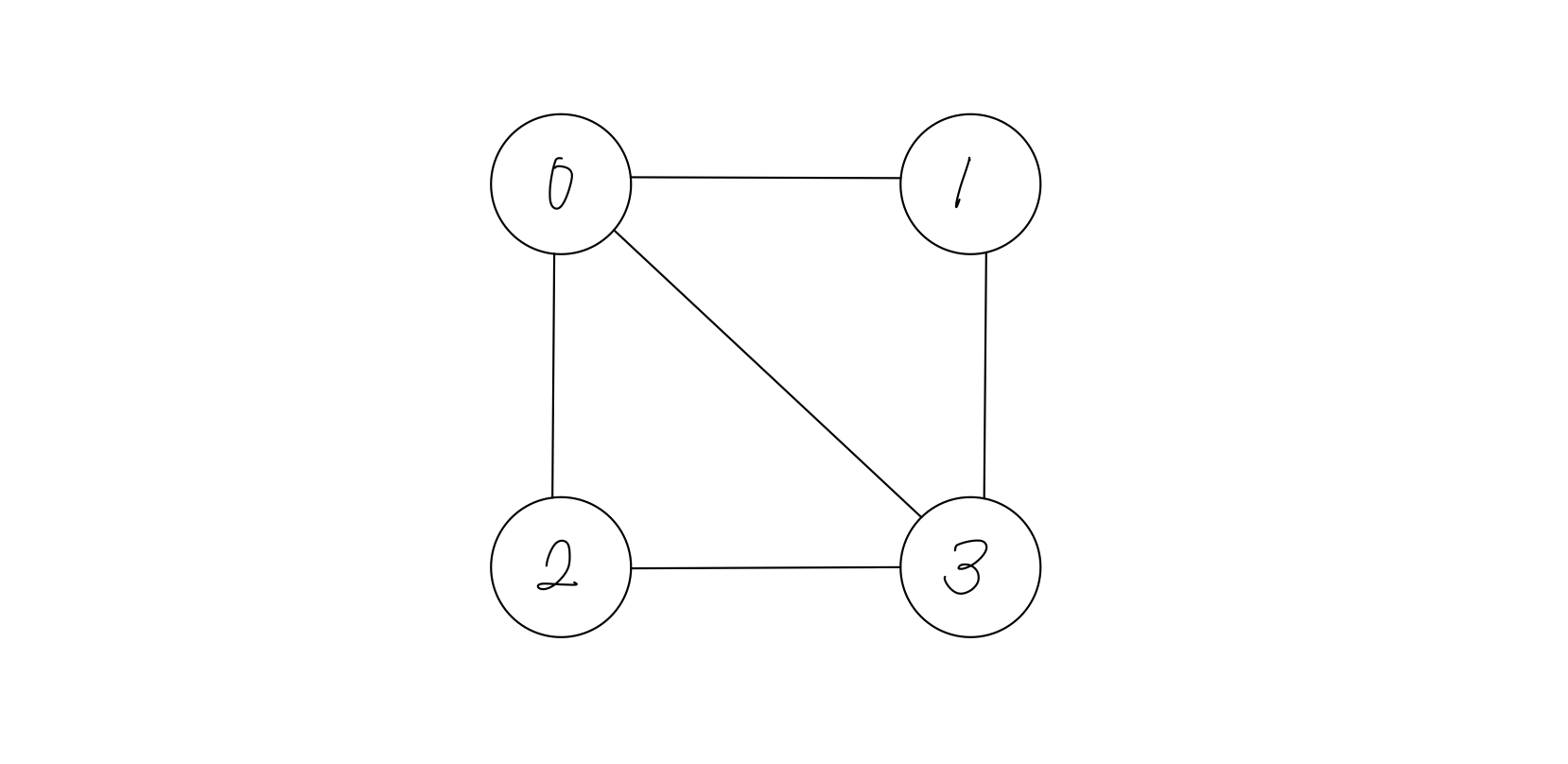
인접행렬
이 그래프를 인접 행렬로 나타낸 것은 아래와 같습니다.
graph = [[0, 1, 1, 1],
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 1, 1, 0]]- 인접행렬의 각 행과 열은 노드를 의미합니다.
- 즉 0번째 노드와 1번째 노드가 연결되었다면, 0행 1열에 1을 입력하고, 입력되지 않았다면 0을 입력하는 것입니다.
- 무향 그래프일 경우 대각선 대칭이지만, 유향그래프일 경우에는 대각선 대칭이 아닙니다.
- 가중치 그래프의 경우에는 1이 아닌 다른 값을 넣음으로써 가중치를 표현할 수 있습니다.
인접리스트
graph = [
[1, 2, 3],
[0, 3],
[0, 3],
[0, 1, 2]
]- 인접리스트는 각각의 인덱스에 헤당하는 노드에 연결된 노드들을 리스트형태로 저장하는 방식입니다.
- 노드를 문자열로 나타내었을 때 Dictionary를 활용할 수 있어서 편리합니다.
- 가중치 그래프에서 가중치를 표현하기 위해서 연결정보에 튜플형태나 다른 방식으로 가중치를 추가적으로 입력해야 합니다.
비교
- 모든 연결정보를 찾아야 하는 경우
- 인접행렬은 각 행에 연결된 노드가 무엇인지 찾기 위해서 모든 노드가 연결되어 있는지 직접확인해야 하기 때문에 시간복잡도가 높습니다.
- 인접리스트는 해당 노드에 입력된 리스트 전체를 가져오면 되기 때문에 시간복잡도가 낮습니다. 즉, 이 경우에는 인접리스트가 더 좋은 성능을 보여줍니다. - 특정 노드 간의 연결정보를 찾아야 하는 경우
- 인접행렬은 graph[i][j]를 통해 i노드와 j노드가 연결되어 있는지 확인할 수 있습니다.
- 반면에 인접리스트는 graph[i]에서 j가 있는지 한번 순회하여 확인해야 하기 때문에 인접행렬을 사용한 경우보다 시간이 오래 걸립니다.
dfs와 bfs 문제(백준 1260)
 dfs와 bfs를 구현하고 경로를 출력하는 문제입니다.
dfs와 bfs를 구현하고 경로를 출력하는 문제입니다.
dfs 구현하기
dfs를 아래의 4가지 방법으로 구현해보겠습니다.
- 인접행렬, stack 자료구조
- 인접행렬, 재귀함수
- 인접리스트, stack 자료구조
- 인접리스트, 재귀함수
인접행렬, stack 자료구조
- 먼저 인접행렬을 만들었습니다.
- visited를 만들어 각 노드에 방문한 적 있는지를 확인하도록 했습니다.
- 노드의 인덱스가 1부터 시작하기 때문에 인접행렬 matrix와 visited의 크기를 각각 1 추가해서 만들었습니다.
n, m, v = map(int, input().split())
matrix = [[0] * (n+1) for _ in range(n+1)]
visited = [False] * (n+1)
for _ in range(m):
f, t = map(int, input().split())
matrix[f][t] = matrix[t][f] = 1
def dfs(matrix, i, visited):
stack=[i]
while stack:
value = stack.pop()
if not visited[value]:
print(value, end=' ')
visited[value] = True
for c in range(len(matrix[value])-1, -1, -1):
# 문제에서 작은 숫자부터 입력하기를 요구해서 반대로 순회했습니다.
# 순차적으로 하면 스택에 2,3,4 순으로 입력되고 4부터 pop되어
# 가장 큰 수인 4부터 pop되기 때문입니다.
if matrix[value][c] == 1 and not visited[c]:
stack.append(c)
dfs(matrix, v, visited)인접행렬, 재귀함수
- 재귀함수를 사용하면 앞선 프로세스가 스택으로 쌓이는 형태가 되기 때문에, stack을 직접 사용하지 않아도 됩니다.
- 코드가 간결해지는 것을 확인할 수 있습니다.
n, m, v = map(int, input().split())
matrix = [[0] * (n+1) for _ in range(n+1)]
visited = [False] * (n+1)
for _ in range(m):
f, t = map(int, input().split())
matrix[f][t] = matrix[t][f] = 1
def dfs(matrix, i, visited):
visited[i] = True
print(i, end=' ')
for c in range(len(matrix[i])):
if matrix[i][c] == 1 and not visited[c]:
dfs(matrix, c, visited)
dfs(matrix, v, visited)인접리스트, stack 자료구조
- 인접리스트를 이중 list로 구현했습니다.
- 인접행렬과 마찬가지로 n+1개의 노드를 만들었습니다.
- 인접행렬에서 모든 행을 반복문으로 확인하여 연결정보를 얻은 것과는 달리, graph[value] 한번 만으로 모든 연결 정보를 가져왔습니다.
n, m, v = map(int, input().split())
graph = [[]] * (n+1)
visited = [False] * (n+1)
for _ in range(m):
f, t = map(int, input().split())
if graph[f] == []:
graph[f] = [t]
else:
graph[f].append(t)
if graph[t] == []:
graph[t] = [f]
else:
graph[t].append(f)
def dfs_stack(graph, i, visited):
stack = [i]
visited[i] == True
while stack:
value = stack.pop()
if not visited[value]:
print(value, end=' ')
visited[value] = True
for j in graph[value]:
if not visited[j]:
stack.append(j)
for i in graph: # 앞서 인접행렬에서 거꾸로 순회했던 이유가 같습니다.
i.reverse()
dfs(graph, v, visited)
인접리스트 재귀함수
n, m, v = map(int, input().split())
graph = [[]] * (n+1)
visited = [False] * (n+1)
for _ in range(m):
f, t = map(int, input().split())
if graph[f] == []:
graph[f] = [t]
else:
graph[f].append(t)
if graph[t] == []:
graph[t] = [f]
else:
graph[t].append(f)
def dfs(graph, i, visited):
visited[i] = True
print(i, end=' ')
for j in graph[i]:
if not visited[j]:
dfs(graph, j, visited)
dfs(graph, v, visited)bfs 구현하기
bfs를 아래의 2가지 방법으로 구현해보겠습니다.
- 인접행렬, queue 자료구조
- 인접리스트, queue 자료구조
인접행렬, queue 자료구조
n, m, v = map(int, input().split())
matrix = [[0] * (n+1) for _ in range(n+1)]
visited = [False] * (n+1)
for _ in range(m):
f, t = map(int, input().split())
matrix[f][t] = matrix[t][f] = 1
from collections import deque
def bfs(matrix, i, visited):
queue= deque()
queue.append(i)
while queue:
value = queue.popleft()
if not visited[value]:
print(value, end=' ')
visited[value] = True
for c in range(len(matrix[value])):
if matrix[value][c] == 1 and not visited[c]:
queue.append(c)인접리스트, queue 자료구조
n, m, v = map(int, input().split())
graph = [[]] * (n+1)
visited = [False] * (n+1)
for _ in range(m):
f, t = map(int, input().split())
if graph[f] == []:
graph[f] = [t]
else:
graph[f].append(t)
if graph[t] == []:
graph[t] = [f]
else:
graph[t].append(f)
from collections import deque
def bfs(graph, i, visited):
queue= deque()
queue.append(i)
while queue:
value = queue.popleft()
if not visited[value]:
print(value, end=' ')
visited[value] = True
for j in graph[value]:
queue.append(j)
bfs(graph, v, visited)다음포스팅
- 좌표평면 or 좌표공간에서 dfs, bfs 구현하기( ex)백준 토마토 )
