플로이드-워셜 알고리즘 with python

최단경로 알고리즘

흔히 알려진 최단경로 알고리즘에는 다익스트라 알고리즘이 있습니다. 다익스트라 알고리즘은 하나의 노드에서 다른 모든 노드로의 최단거리를 구할 때 사용하는 알고리즘입니다. 반면에, 플로이드-워셜 알고리즘은 모든 노드에서 다른 모든 노드까지의 최단거리를 구할 때 사용하는 알고리즘입니다. 플로이드-워셜 알고리즘을 구현하는 것은 매우 단순하기 때문에, 그래프 내에서 모든 거리정보가 필요할 때는 플로이드 알고리즘을 사용하는 것이 좋습니다.

플로이드-워셜 알고리즘

• 플로이드 워셜 알고리즘은 거쳐가는 노드를 기준으로 거리를 구합니다.
• 특정 노드를 거쳤을때의 거리들과 하나의 간선만으로 해당 다른 노드에 도달했을 때를 비교하여, 가장 작은 값을 최단 거리로 지정하는 방법입니다.
• 구현을 할 때에는 거리를 표현하는 행렬의 값을 계속해서 갱신하는 방식으로, 다이나믹 프로그래밍에 해당하는 알고리즘입니다.
• 플로이드 워셜 알고리즘의 점화식은 아래와 같습니다.

---

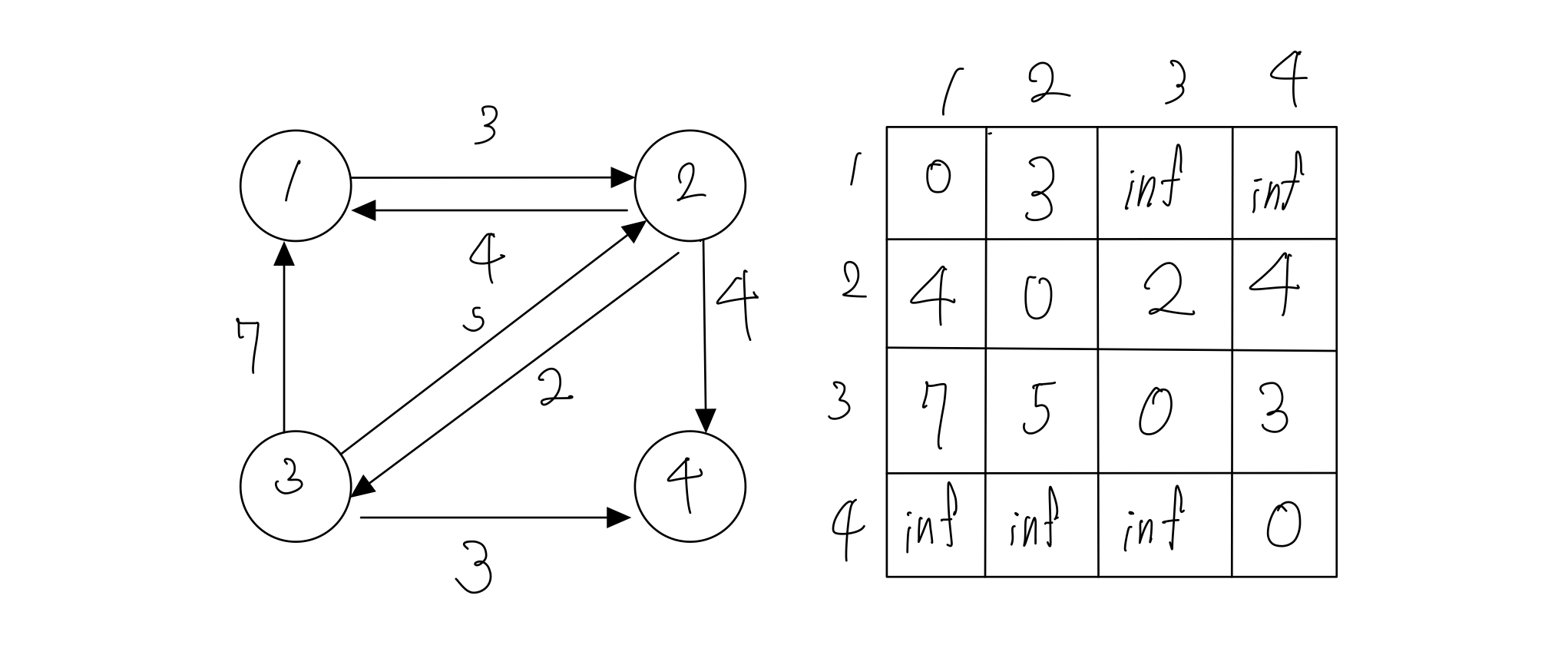
• 플로이드 알고리즘을 구현하기 위해서는 우선 간선하나만으로 갈 수 있는 거리를 모두 행렬에 넣어야 합니다.
  

1. 위의 점화식을 활용하여 값을 구해보면, 1번 노드를 거칠 때는 행렬이 갱신되지 않습니다.
   
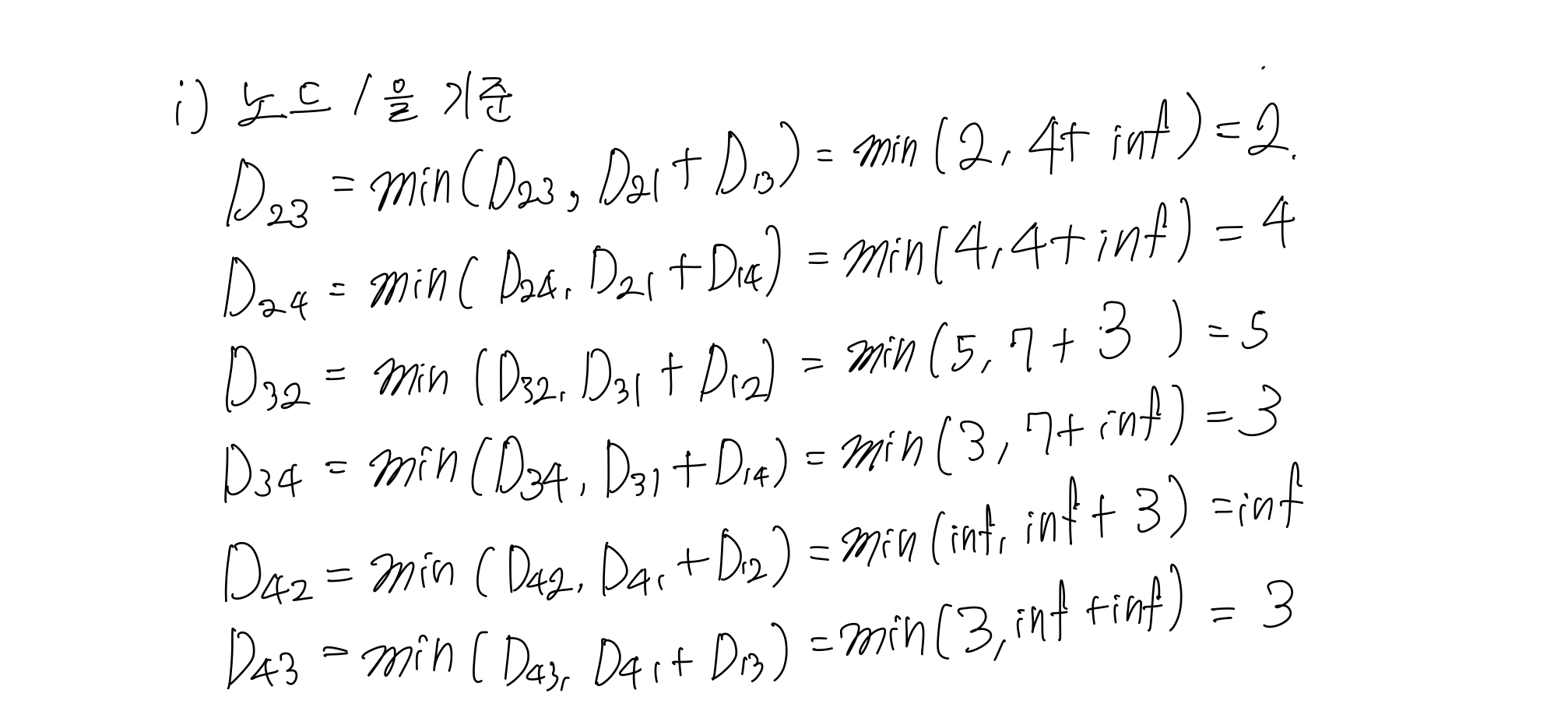
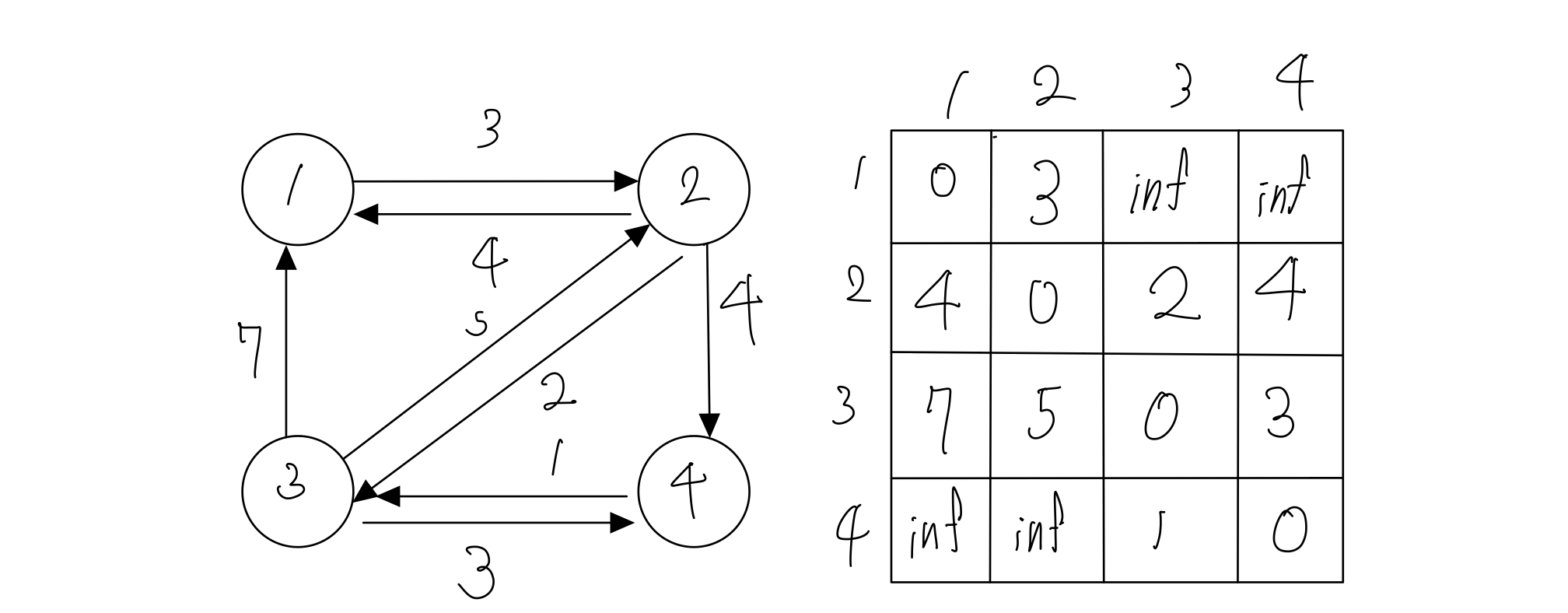
2. 2번 노드를 거칠 때는 행렬의 값이 일부 갱신됩니다.
   
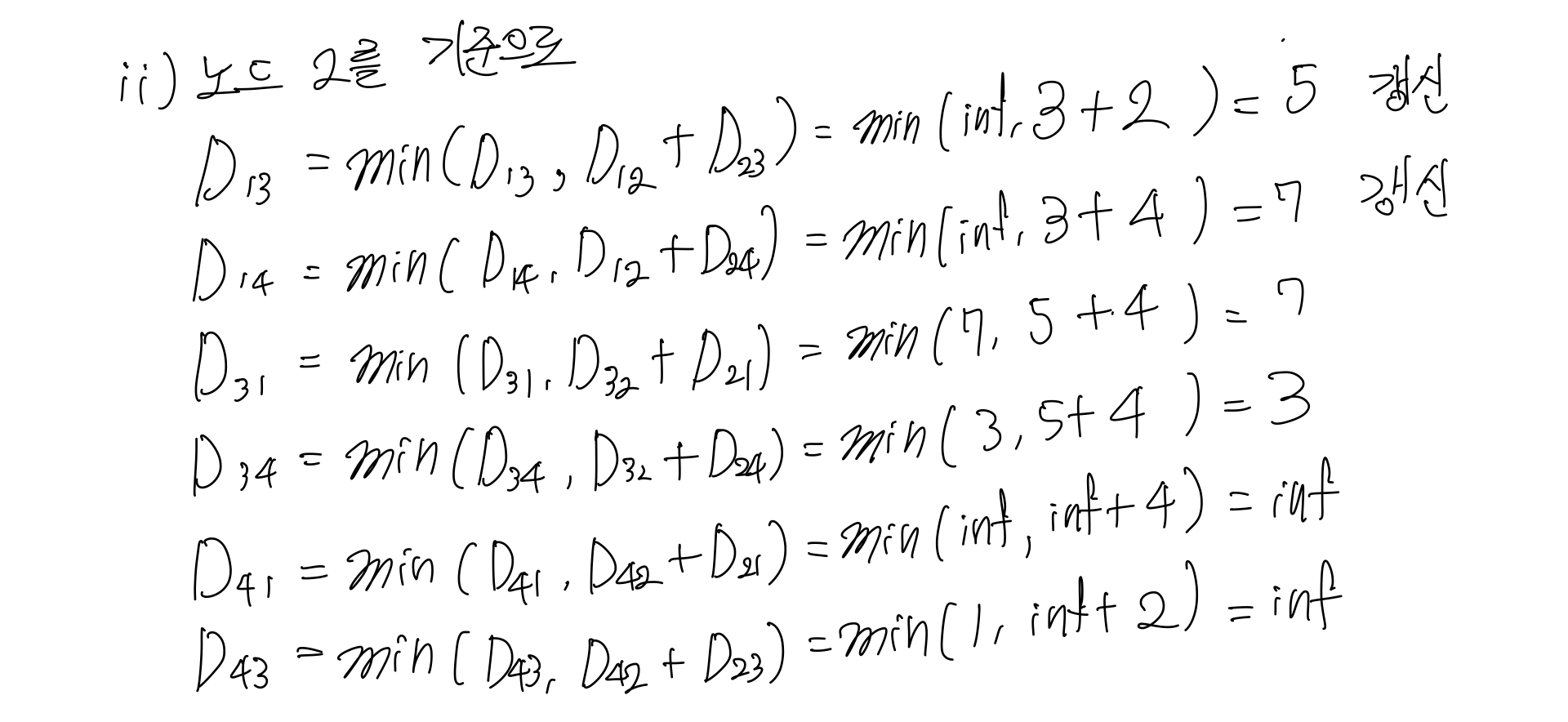
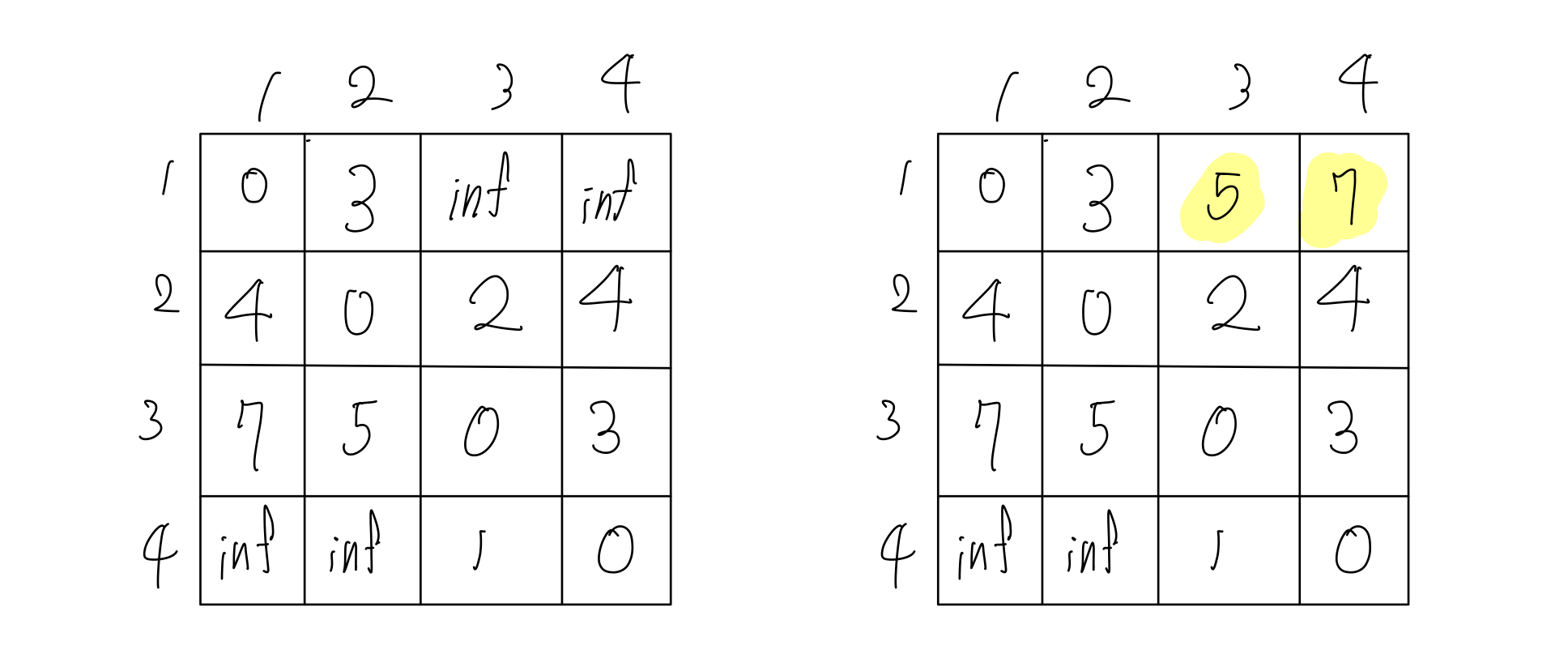
3. 이런 식으로 4번쩨 노드까지 반복하면 아래와 같이 최단거리에 대한 정보를 담은 행렬이 완성됩니다.
   
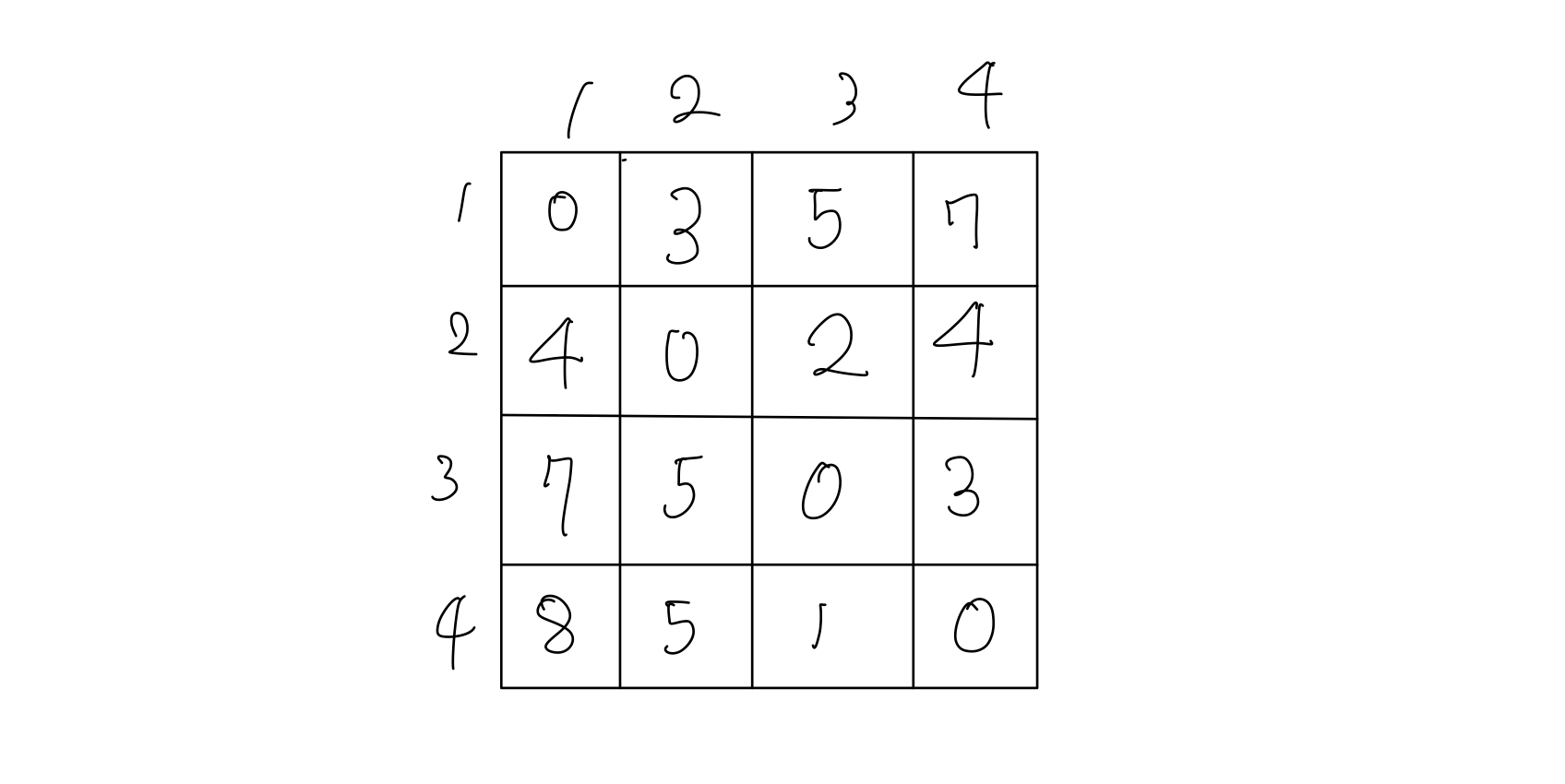
   아래의 문제를 풀어보면서 플루이드 워셜 알고리즘을 구현해보겠습니다.

케빈 베이컨의 6단계 법칙

n, m = map(int, input().split())

matrix = [[n]*n for _ in range(n)]        # INF를 n으로 표현했습니다.
                                          # 최단 거리는 노드의 개수보다 커질수 없기 때문입니다. 
for _ in range(m):
  a,b = map(int, input().split())
  matrix[a-1][b-1] = matrix[b-1][a-1] = 1 # 연결된 노드끼리의 거리는 모두 1입니다.
  										  # 무방향 그래프이므로 대각선 대칭으로 값을 입력합니다.
 
for i in range(n):
  matrix[i][i] = 0                        # 대각선을 0으로 초기화

for k in range(n):
  for i in range(n):
    for j in range(n):
      if matrix[i][j] > matrix[i][k] + matrix[k][j]:
        matrix[i][j] = matrix[i][k] + matrix[k][j]

result = []
for i in (matrix):
  result.append(sum(i))

print(result.index(min(result))+1)