위상정렬(Topology Sort) 알고리즘 with python(heap, queue, stack)

cyr·2021년 12월 29일

Topology Sort algorithm 알고리즘 위상정렬

위상정렬이란?

정렬 알고리즘의 일종으로, 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용하는 알고리즘입니다.
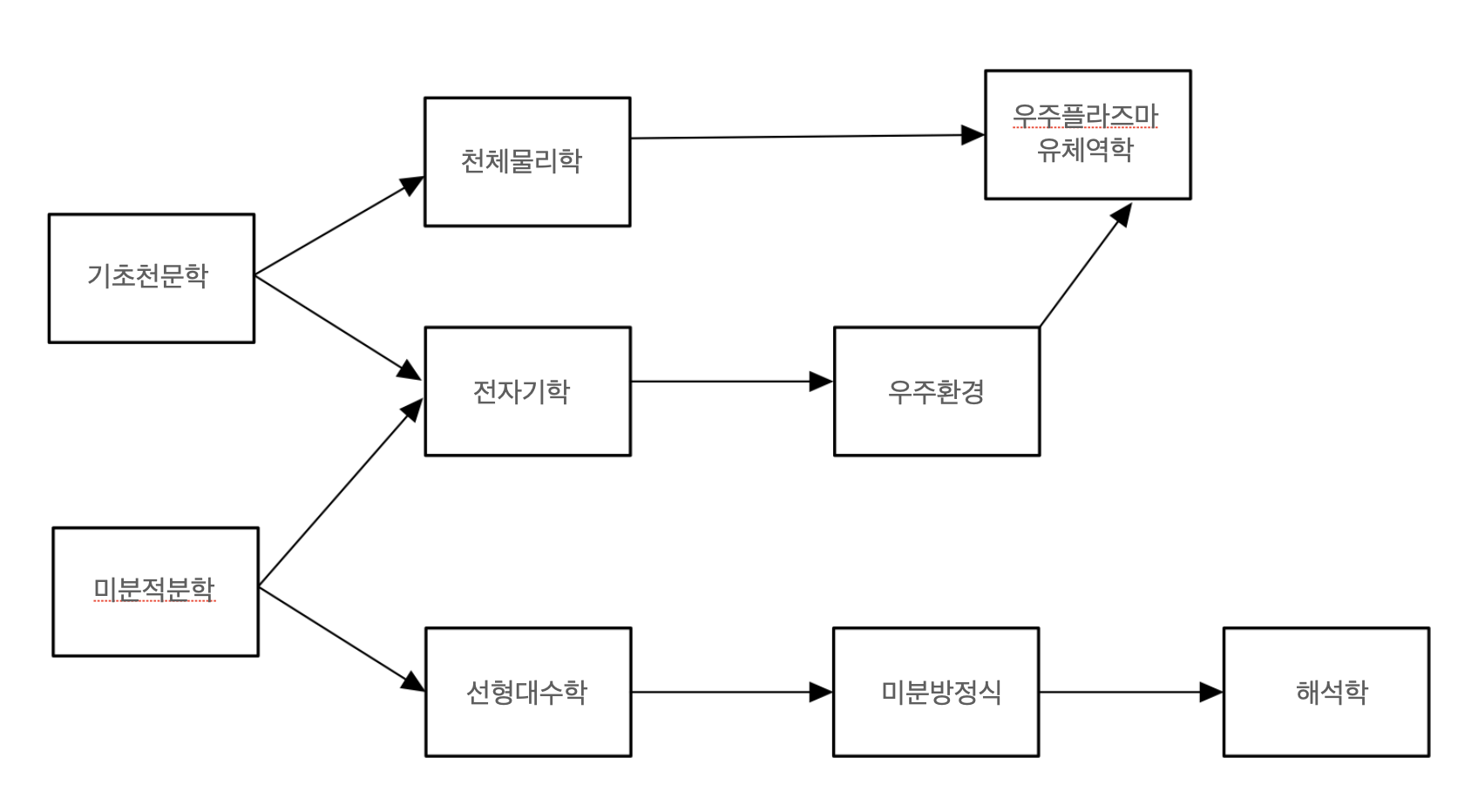
어떤 업무들에 선후관계가 있을 때 사용하는 알고리즘으로, 아래 그림과 같은 대학교 강의의 선수후수 과목을 예시로 들 수 있습니다.
위의 그림에 따르면 전자기학 과목을 듣기 위해서는 기초천문학과 미분적분학을 반드시 수강해야합니다.
선수과목들은 후수과목을 듣기 위한 조건이라고도 생각할 수 있습니다. 즉, 남아있는 선수과목이 하나도 없어야 후수과목을 수강할 수 있습니다.

위상정렬 알고리즘 설명

위 그림의 과목들을 숫자로 단순화 해보겠습니다.

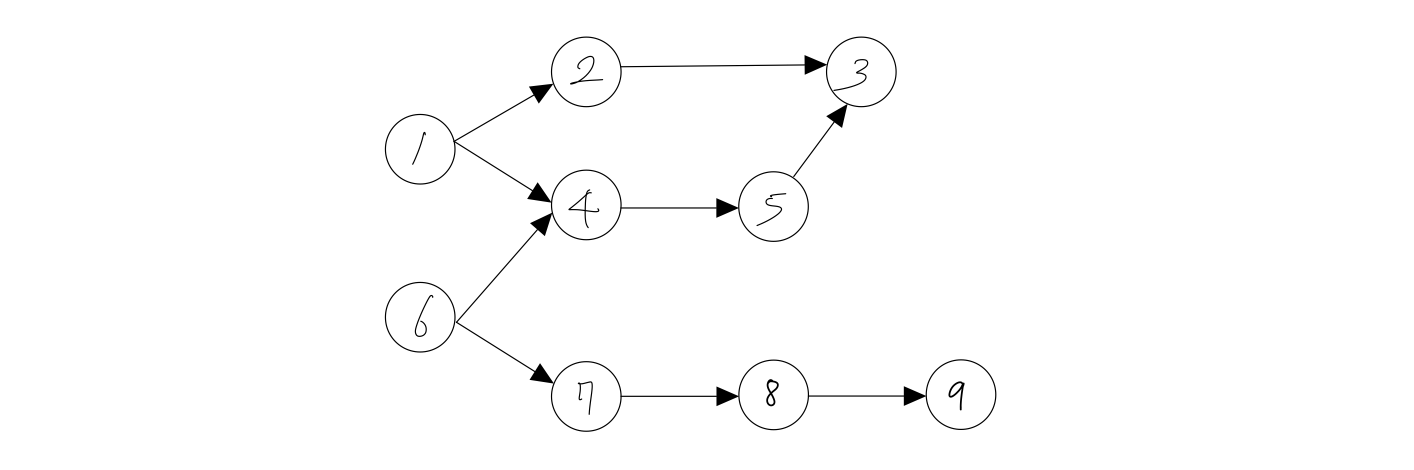
진입하는 간선이 없는 노드를 큐에 담는다.

큐에서 노드를 꺼내고 노드에 연결된 간선을 없앤다.

1번과 2번을 반복한다.

여기서 큐에서 꺼내진 순서가 위상정렬을 수행한 결과가 됩니다.

그림을 통해 과정을 보겠습니다.

그래프

노드	진출차선이 향하는 노드
1	2, 4
2	3
3
4	5
5	3
6	4, 7
7	8
8	9
9

노드별 진입차수의 개수

1	2	3	4	5	6	7	8	9
0	1	2	2	1	0	1	1	1

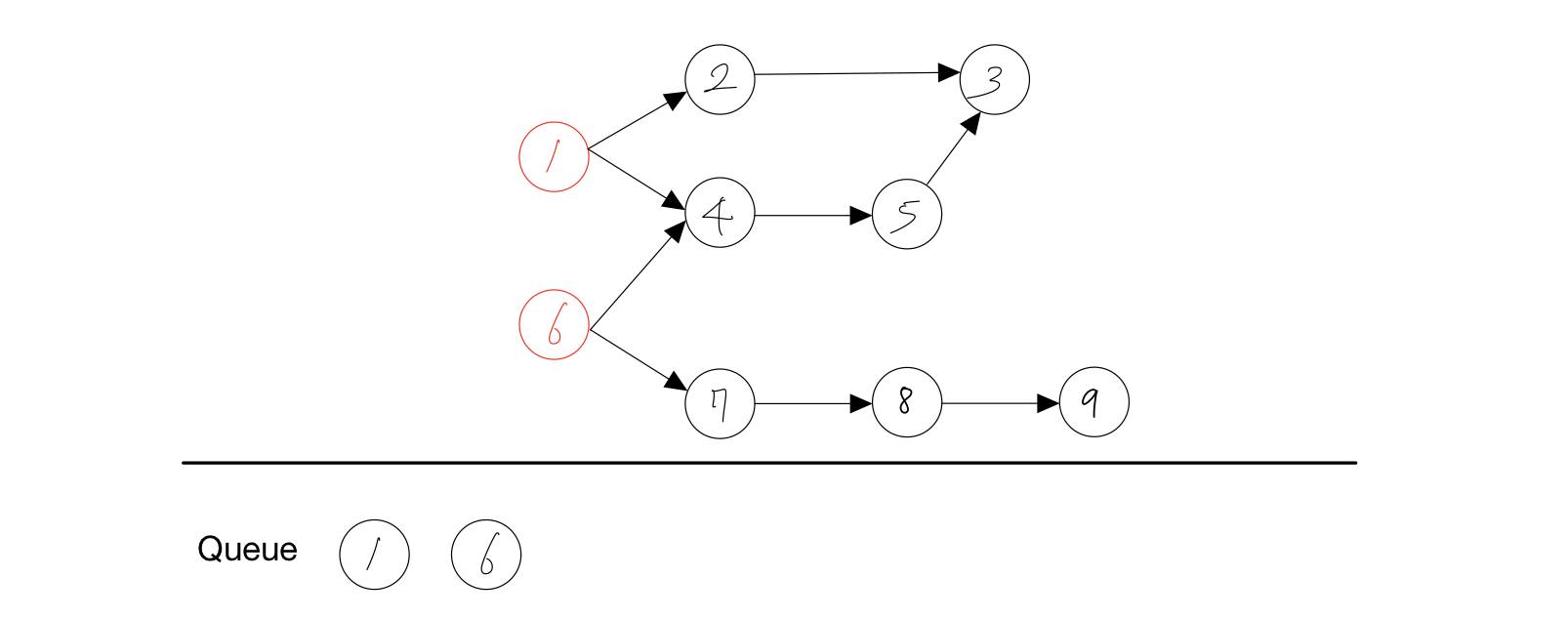
진입차수가 없는 노드인 1과 6을 Queue에 담는다.

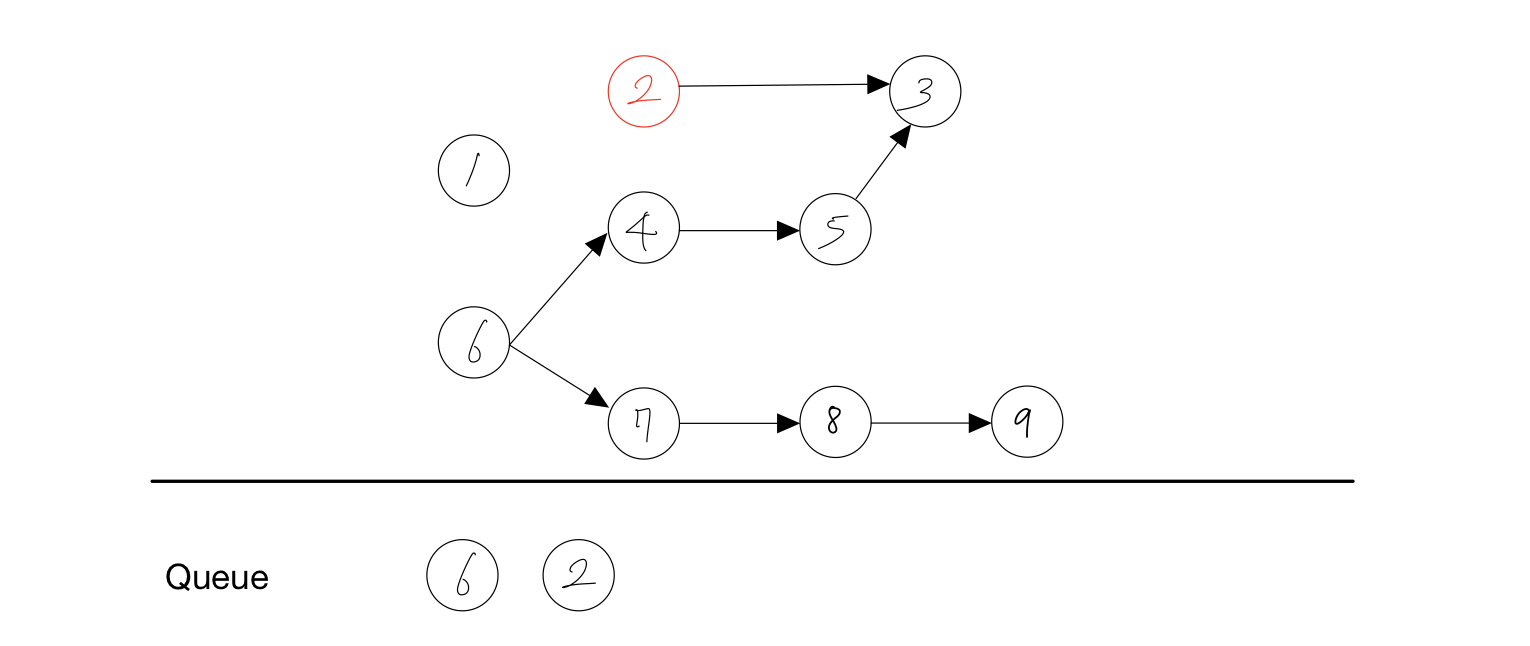
노드 1을 Queue에서 제거한다.
노드 1에 붙어있던 간선을 제거한다.
간선을 제거하여 노드 2와 4의 진입차수가 하나 줄어든다.

1	2	3	4	5	6	7	8	9
0	0	2	1	1	0	1	1	1

진입차수가 0이 된 노드인 2를 Queue에 담는다.

결과 : 1

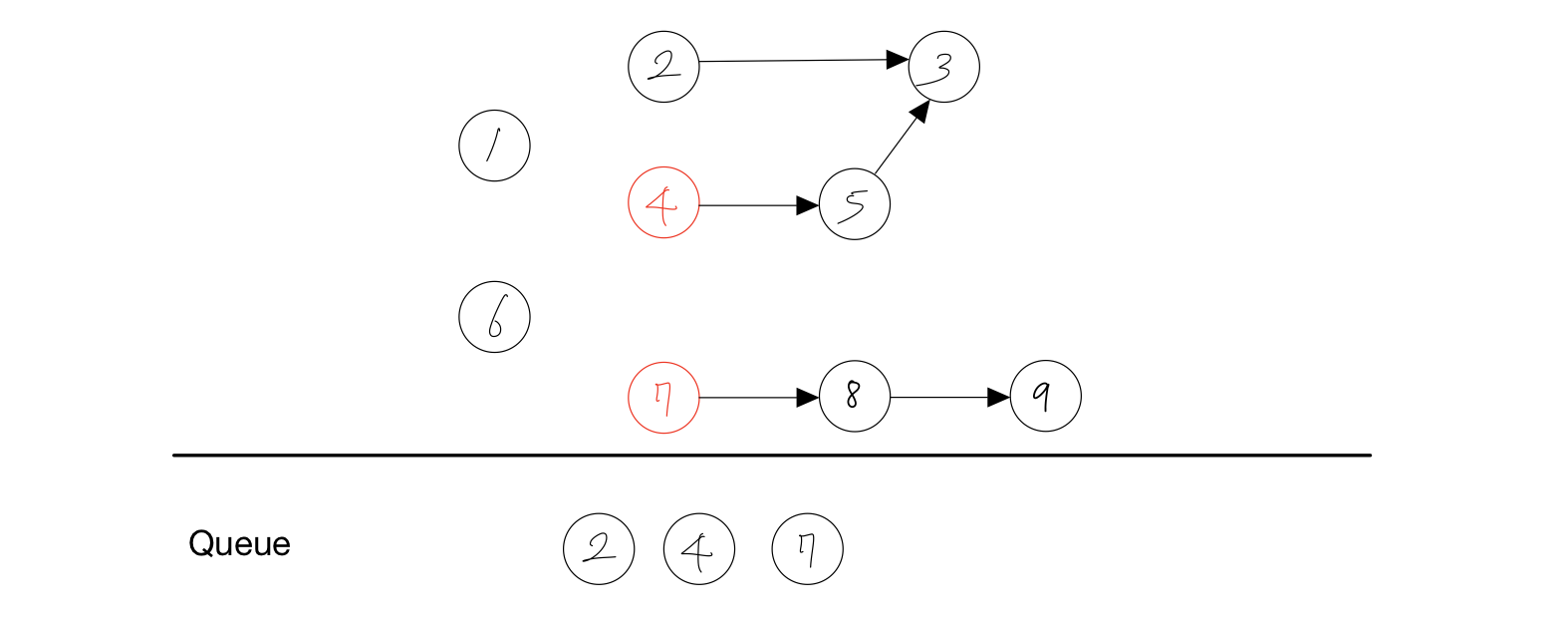
노드 6을 Queue에서 제거한다.
노드 6에 붙어있던 간선을 제거한다.
간선을 제거하여 노드 4와 7의 진입차수가 하나 줄어든다.

1	2	3	4	5	6	7	8	9
0	0	2	0	1	0	0	1	1

진입차수가 0이 된 노드인 4와 7을 Queue에 담는다.

결과 : 1, 6

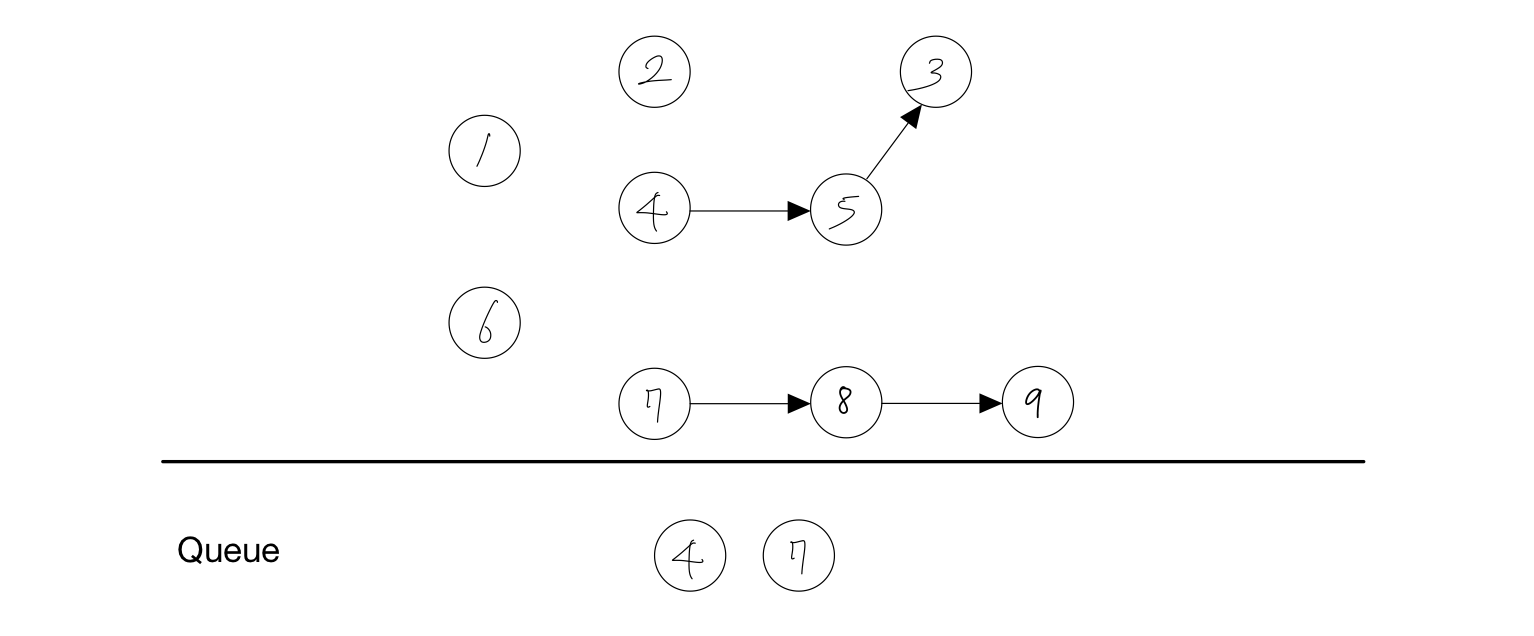
노드 2를 Queue에서 제거한다.
노드 2에 붙어있던 간선을 제거한다.
간선을 제거하여 노드 3 진입차수가 하나 줄어든다.

1	2	3	4	5	6	7	8	9
0	0	1	0	1	0	0	1	1

진입차수가 없는 노드가 없으므로 다음으로 넘어간다.

결과 : 1, 6, 2

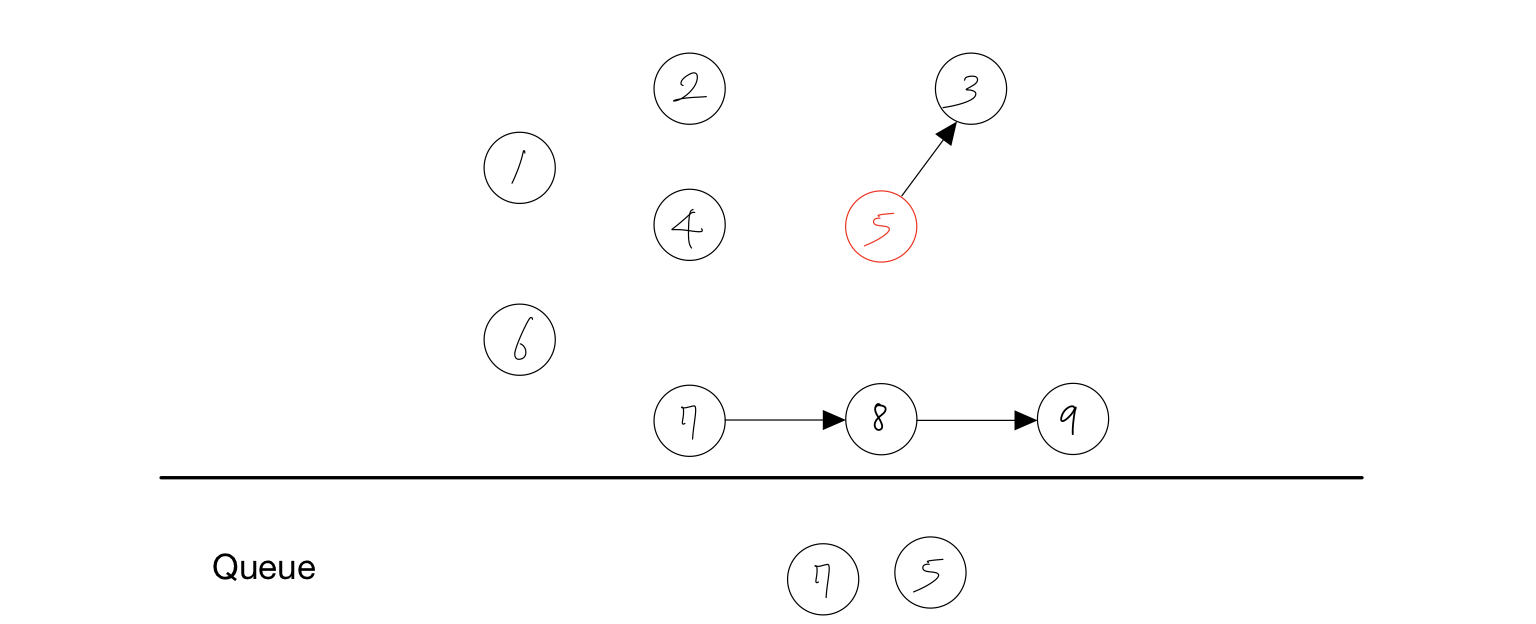
노드 4를 Queue에서 제거한다.
노드 4에 붙어있던 간선을 제거한다.
간선을 제거하여 노드 5의 진입차수가 하나 줄어든다.

1	2	3	4	5	6	7	8	9
0	0	1	0	0	0	0	1	1

진입차수가 없는 노드인 5를 Queue에 담는다.

결과 : 1, 6, 2, 4

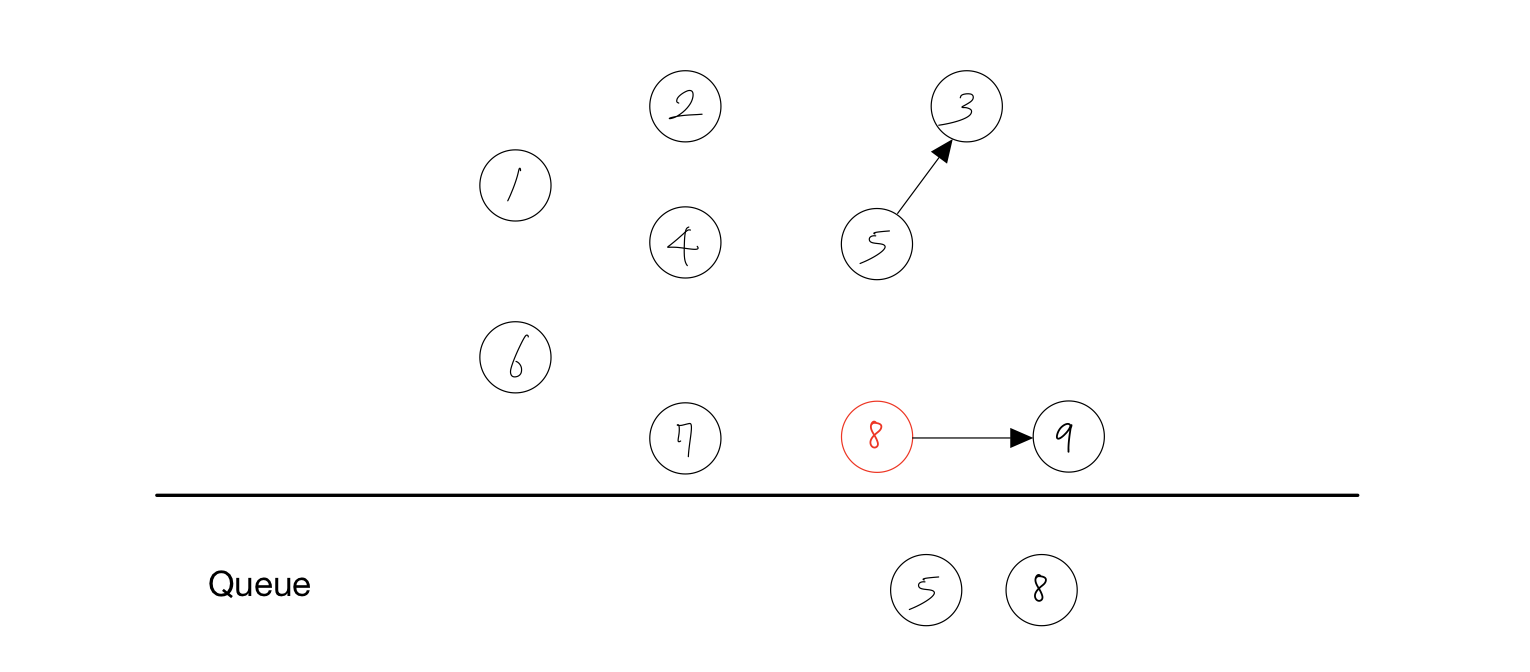
노드 7를 Queue에서 제거한다.
노드 7에 붙어있던 간선을 제거한다.
간선을 제거하여 노드 8의 진입차수가 하나 줄어든다.

1	2	3	4	5	6	7	8	9
0	0	1	0	0	0	0	0	1

진입차수가 0이 된 노드인 8을 Queue에 담는다.

결과 : 1, 6, 2, 4, 7

노드 5를 Queue에서 제거한다.
노드 5에 붙어있던 간선을 제거한다.
간선을 제거하여 노드 3의 진입차수가 하나 줄어든다.

1	2	3	4	5	6	7	8	9
0	0	0	0	0	0	0	0	1

진입차수가 0이 된 노드인 3을 Queue에 담는다.

결과 : 1, 6, 2, 4, 7, 5

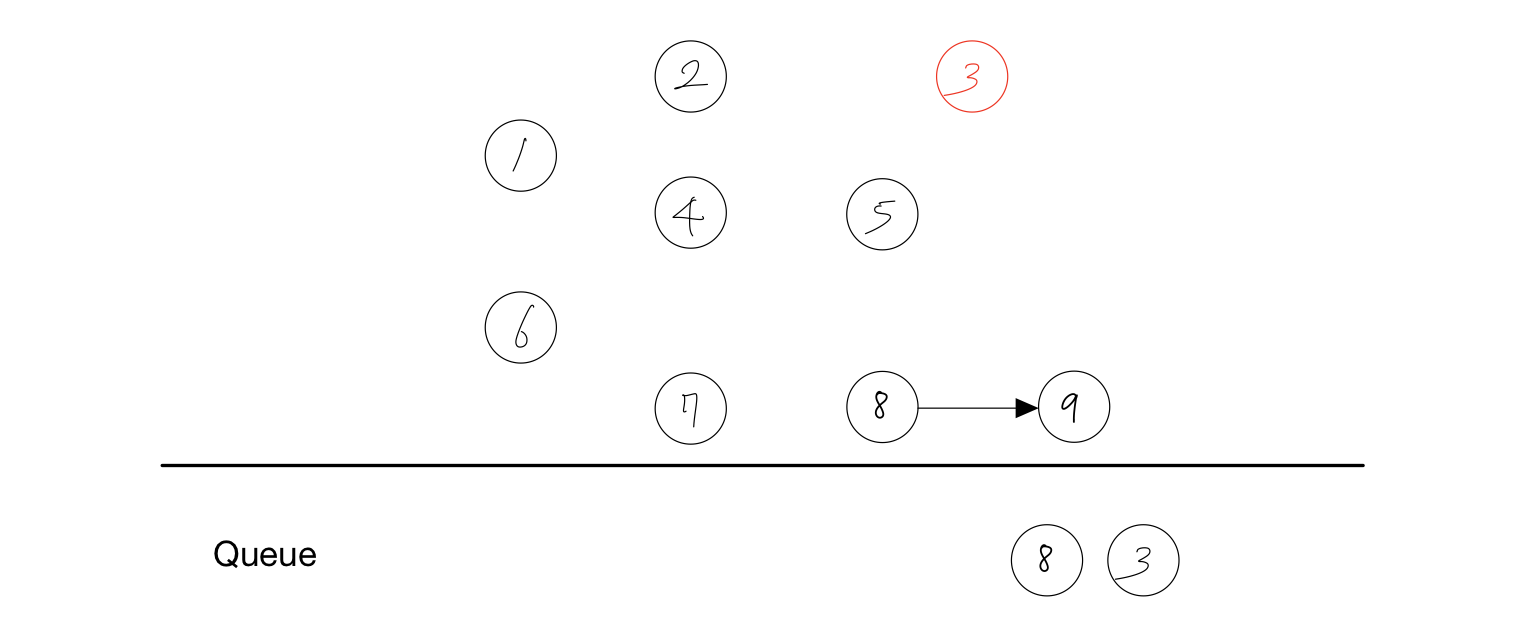
노드 8를 Queue에서 제거한다.
노드 8에 붙어있던 간선을 제거한다.
간선을 제거하여 노드 9의 진입차수가 하나 줄어든다.

1	2	3	4	5	6	7	8	9
0	0	0	0	0	0	0	0	0

진입차수가 0이 된 노드인 9를 Queue에 담는다.

결과 : 1, 6, 2, 4, 7, 5, 8

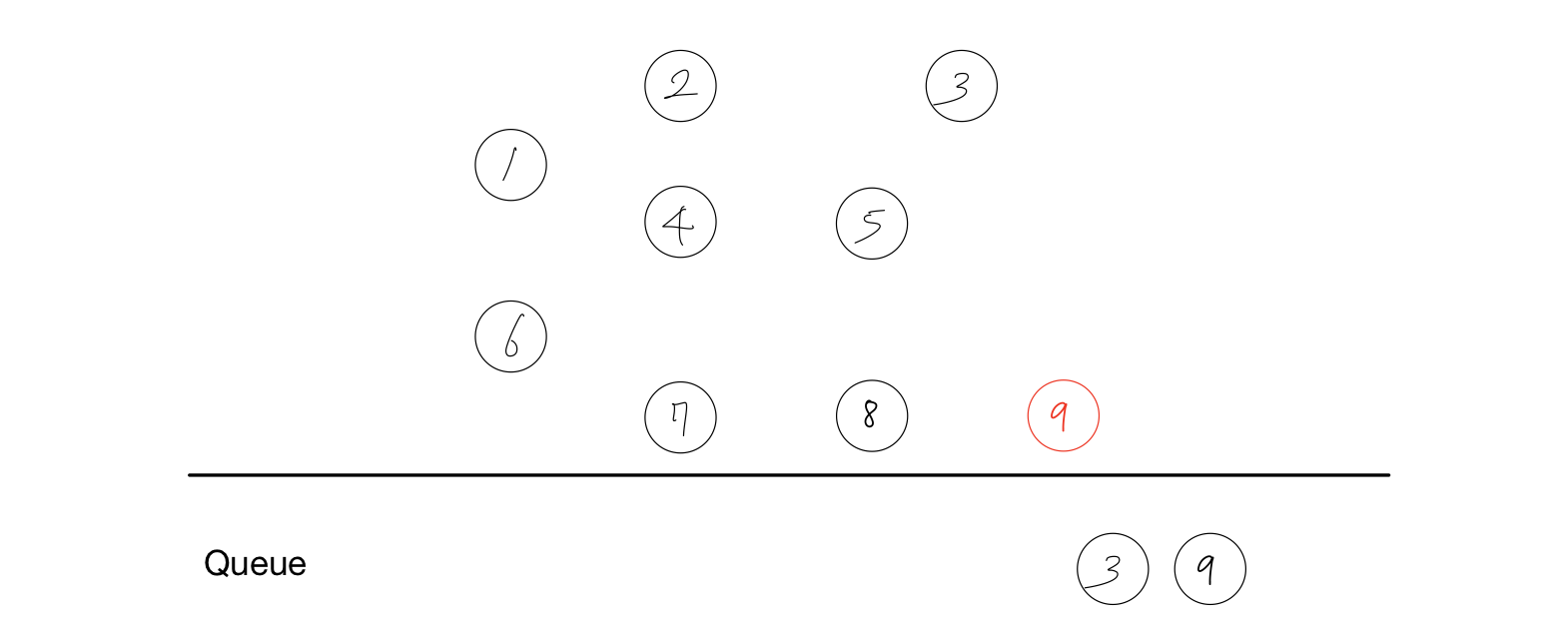
노드 3를 Queue에서 제거한다.
노드 3에는 간선이 없으니 넘어간다.

결과 : 1, 6, 2, 4, 7, 5, 8, 3

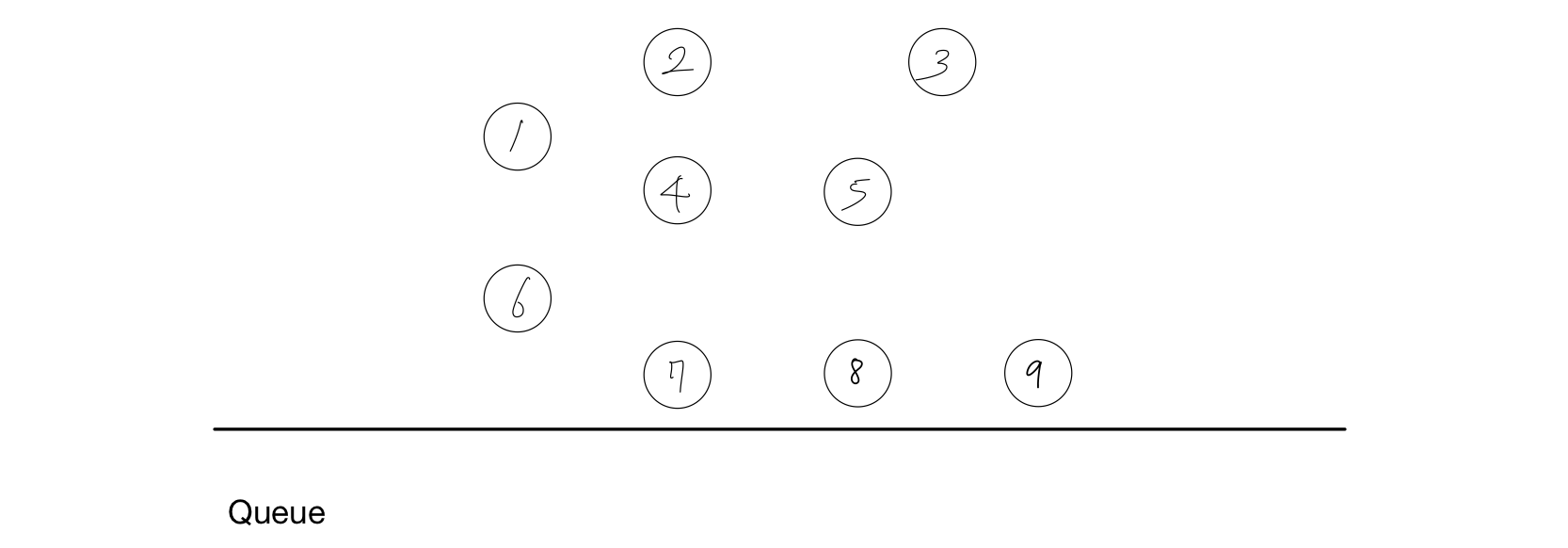
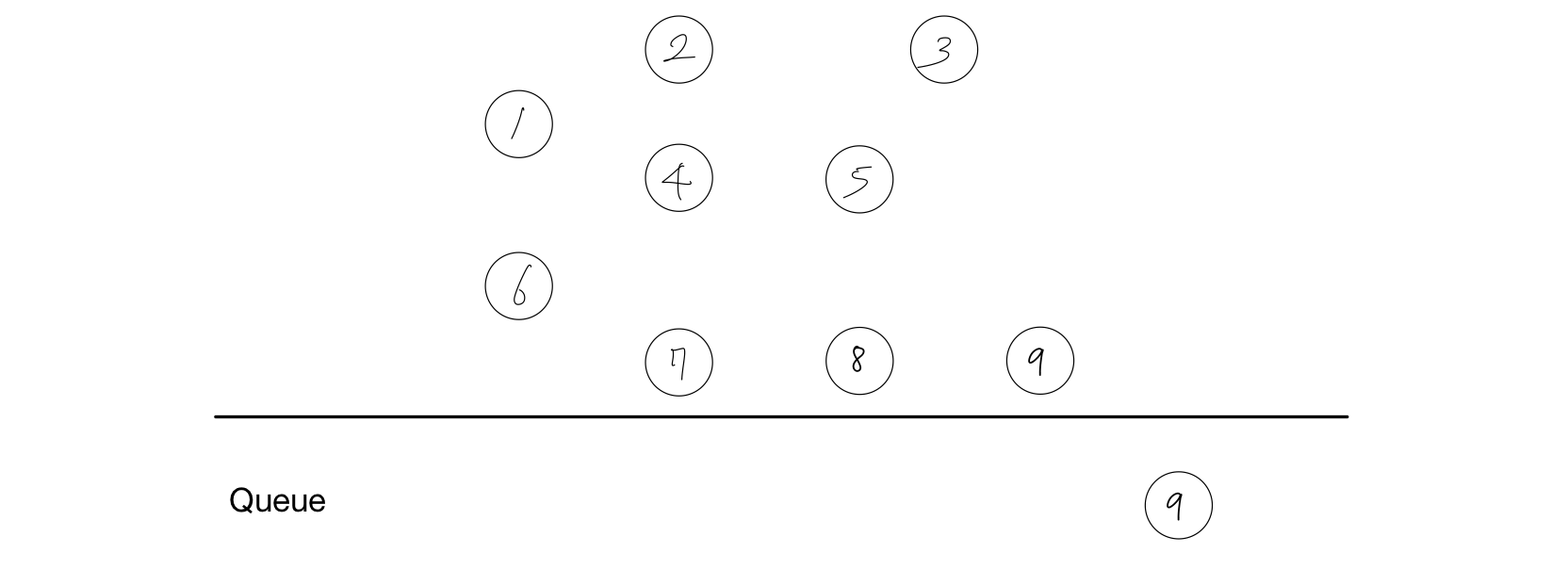
노드 9를 Queue에서 제거한다.
노드 9에는 간선이 없으니 넘어간다.

결과 : 1, 6, 2, 4, 7, 5, 8, 3, 9

우리가 얻으려고 한 결과값은 큐에서 빠진 순서대로 나열한 것입니다.
따라서 모든 과목을 듣기위해 수강 신청을 하는 순서는 아래왜 같습니다.

1 -> 6 -> 2 -> 4 -> 7 -> 5 -> 8 -> 3 -> 9
기초천문학 -> 미분적분학 -> 천체물리학 -> 전자기학 -> 선형대수학 -> 우주환경 -> 미분방정식 -> 우주플라즈마 유체역학 -> 해석학

이 결과를 보고 다른 경우도 답이 될 수 있지 않냐고 물을 수 있습니다. 그 말은 사실입니다.
가령 1 -> 2 -> 6 -> 4 -> 7 -> 8 -> 9 -> 5 -> 3 과 같이 조건만 만족한다면 특별한 규칙없이 낸 결론 또한 답이 될 수도 있습니다.

따라서 해당 알고리즘을 사용해서 코딩테스트 문제를 풀 때는, 문제의 조건을 잘 읽고 어떤 알고리즘을 통해 풀어야 문제에서 원하는 경로대로 결론을 낼 수 있는지 파악할 필요가 있습니다.

이 문제를 풀 때는 큐를 사용하여 풀었지만, 스택이나 힙을 사용해서도 풀 수 있습니다.

여기서 소개한 방법처럼 큐를 사용한다면 너비우선적으로 경로가 작성될 것입니다.
stack을 사용한다면, 깊이 우선적으로 경로가 작성됩니다.
Heap을 사용한다면, 각 노드의 값에서 나올 수 있는 값 중 가장 작은 값들 부터 탐색하는 방식으로 경로가 작성될 것입니다.

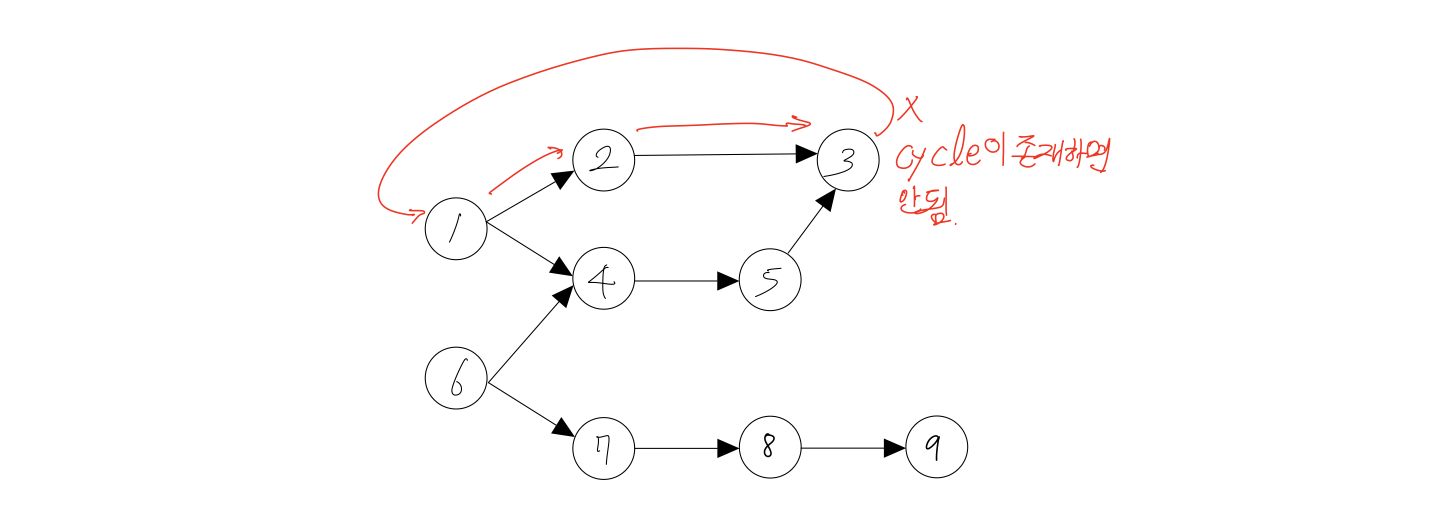
마지막으로 위상정렬 알고리즘을 사용하기 위해서는 그래프 내에 사이클이 존재해서는 안됩니다. 사이클이 존재한다면, 이미 지나간 경로를 다시 지나가는 경우가 발생하기 때문에 위상정렬 알고리즘을 사용할 수 없습니다.

위상정렬 알고리즘 구현

위상정렬 알고리즘을 코드로 구현해보겠습니다.
데이터 입력 형식은 아래와 같습니다.
첫째 줄에 노드의 개수 n과 간선의 갯수 m을 입력합니다.
그 아래에 연결될 노드에 대한 정보들을 한 줄씩 입력합니다.(즉, m개의 줄을 입력한다.)

입력예시 (알고리즘 설명의 예시와 동일한 예시입니다.)
9 9
1 2
2 3
1 4
4 5
5 3
6 4
6 7
7 8
8 9

queue로 구현

queue로 구현했을 때는 앞서 말한대로 너비우선탐색과 비슷한 방식으로 정렬됩니다.

1, 6, 2, 4, 7, 5, 8, 3, 9

n, m = map(int, input().split())
indegree = [0]*(n+1)              # 진입차수에 대한 정보를 담은 배열을 생성한다.
                                  # 데이터가 1부터 시작하기 때문에 n+1개를 생성했다.
                                  # 각각의 인덱스는 노드의 숫자에 해당하고 인덱스의 값은 진입차수의 개수를 의미한다.

graph = [[] for _ in range(n+1)]  # 각 노드별로 나가는 간선의 위치를 저장한다.
                                  # 각 인덱스는 노드의 숫자에 해당하고 인덱스의 값에 해당하는 배열으로 간선이 이어진다는 것을 의미한다.
                                  # 아래의 반복문을 통해 채워질 것이다.

queue = []                        # 진입차수가 없는 노드가 들어갈 queue 자료구조이다.
result = []                       # queue에서 빠져나온 순서대로 값이 들어갈 것이며, 이것이 정렬의 결과물이다.

for _ in range(m):
  prev, post = map(int, input().split()) # prev는 선행과목, post는 후수과목에 해당한다.
  graph[prev].append(post)        # graph의 prev인덱스에 해당하는 배열에 post를 추가한다. 즉, prev라는 과목이 수강되어야 post를 수강할 수 있다.
  indegree[post]+= 1              # post의 선수과목이 지정되었으므로 진입차수를 1 추가한다.

for i in range(1, n+1):           # 처음에는 먼저 진입차수가 0인 노드부터 찾습니다.
  if indegree[i] == 0:
    queue.append(i)


while queue:                      # queue가 비게 된다면, 정렬이 모두 끝납니다. 그래프 내에 사이클이 존재한다면, queue 가 비지 않게 되고 무한루프를 돕니다.
  value = queue.pop(0)            # queue에서 값을 꺼냅니다.
  result.append(value)            # 결과값으로 저장합니다.
  for i in graph[value]:          # queue에서 꺼내진 값의 다음 노드로 연결된 노드들을 찾습니다.
    indegree[i] -= 1              # queue에서 꺼내진 값에서 나오는 진출간선을 없애줍니다.
    if indegree[i] == 0:          # 이후 진입차수가 0이 된 노드를 찾고
      queue.append(i)             # 해당 노드를 queue에 넣고 queue가 빌 때까지 위의 내용들을 반복합니다.

print(result)

stack으로 구현

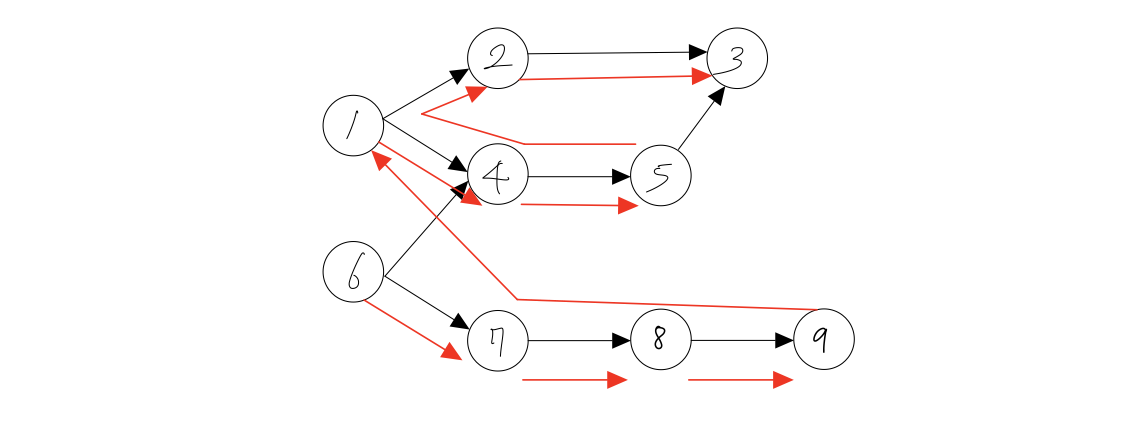
stack로 구현했을 때는 앞서 말한대로 깊이우선탐색과 비슷한 방식으로 정렬됩니다.

6, 7, 8, 9, 1, 4, 5, 2, 3

n, m = map(int, input().split())
indegree = [0]*(n+1)              # 진입차수에 대한 정보를 담은 배열을 생성한다.
                                  # 데이터가 1부터 시작하기 때문에 n+1개를 생성했다.
                                  # 각각의 인덱스는 노드의 숫자에 해당하고 인덱스의 값은 진입차수의 개수를 의미한다.

graph = [[] for _ in range(n+1)]  # 각 노드별로 나가는 간선의 위치를 저장한다.
                                  # 각 인덱스는 노드의 숫자에 해당하고 인덱스의 값에 해당하는 배열으로 간선이 이어진다는 것을 의미한다.
                                  # 아래의 반복문을 통해 채워질 것이다.

stack = []                        # 진입차수가 없는 노드가 들어갈 stack 자료구조이다.
result = []                       # stack에서 빠져나온 순서대로 값이 들어갈 것이며, 이것이 정렬의 결과물이다.

for _ in range(m):
  prev, post = map(int, input().split()) # prev는 선행과목, post는 후수과목에 해당한다.
  graph[prev].append(post)        # graph의 prev인덱스에 해당하는 배열에 post를 추가한다. 즉, prev라는 과목이 수강되어야 post를 수강할 수 있다.
  indegree[post]+= 1              # post의 선수과목이 지정되었으므로 진입차수를 1 추가한다.

for i in range(1, n+1):           # 처음에는 먼저 진입차수가 0인 노드부터 찾습니다.
  if indegree[i] == 0:
    stack.append(i)


while stack:                      # stack 비게 된다면, 정렬이 모두 끝납니다. 그래프 내에 사이클이 존재한다면, stack dl 비지 않게 되고 무한루프를 돕니다.
  value = stack.pop()            # stack에서 값을 꺼냅니다.
  result.append(value)            # 결과값으로 저장합니다.
  for i in graph[value]:          # stack에서 꺼내진 값의 다음 노드로 연결된 노드들을 찾습니다.
    indegree[i] -= 1              # stack에서 꺼내진 값에서 나오는 진출간선을 없애줍니다.
    if indegree[i] == 0:          # 이후 진입차수가 0이 된 노드를 찾고
      stack.append(i)             # 해당 노드를 stack에 넣고 stack가 빌 때까지 위의 내용들을 반복합니다.

print(result)

heap으로 구현

heap으로 구현하면 pop할때의 값이 자료구조에 담긴 값중에 가장 작은 값이 됩니다.
즉, 조건을 만족하는 내에서 가장 숫자가 작은 노드부터 정렬됩니다.
이 예시에서는 queue와 결과값이 같습니다.
heap을 반드시 사용해야 하는 경우는 백준 1776번 문제집에서 확인해볼 수 있습니다.

import heapq
n, m = map(int, input().split())

indegree = [0]*(n+1)
graph = [[] for _ in range(n+1)]
heap = []
result = []
for _ in range(m):
  prev, post = map(int, input().split())
  graph[prev].append(post)
  indegree[post] += 1

for i in range(1,n+1):
  if indegree[i]==0:
    heapq.heappush(heap, i)

while heap:
  value = heapq.heappop(heap)
  result.append(value)
  for i in graph[value]:
    indegree[i] -= 1
    if indegree[i]==0:
      heapq.heappush(heap, i)

for i in result:
  print(i, end=" ")

cyr

개발

이전 포스트

가상머신에 우분투 설치하기

다음 포스트