파이썬에서 부분집합 구하기

백준이나 프로그래머스에서 문제를 풀다보면 부분집합을 구했을때 굉장히 쉽게 풀 수 있는 문제들이 있습니다. 매번 itertools라는 라이브러리를 사용해서 해결했었는데 그마저도 기억이 안나서 구글링해서 해결한 적이 많죠.. 오늘은 이런 사태를 예방하기 위해, 내용도 제대로 숙지할 겸, 제 블로그에 정리해보겠습니다. 먼저 코드를 보여주고 해당코드에 대해 설명해보겠습니다^^

부분집합

파이썬에서 부분집합을 구하는 방법은 여러 가지가 있습니다. 그 중 가장 대표적인 방법 4가지를 소개하고 구현해보겠습니다.

• itertools 라이브러리의 combinations 메서드 사용하기
• 단순 반복문과 배열
• 재귀
• 비트연산

---

1. itertools 라이브러리의 combinations 메서드

from itertools import combinations 

arr = [1, 2, 3]
result = []
for i in range(len(arr)+1):
  result = result+list(combinations(arr,i))  

print(result)
# [(), (1,), (2,), (3,), (1, 2), (1, 3), (2, 3), (1, 2, 3)]

가장 직관적으로 이해되는 방법이어서 평소에 가장 많이 사용해왔던 방법입니다. itertools라는 라이브러리에 있는 combinations를 사용한 방법입니다. combinations의 사용방법은 아래와 같습니다.

from itertools import combinations 

arr = [1,2,3]

print(list(combinations(arr,1)))
#[(1,), (2,), (3,)]

print(list(combinations(arr,2)))
#[(1, 2), (1, 3), (2, 3)]

• combinations 메서드의 첫번째 인자로 대상 리스트를 넣고,

• 두번째 인자로는 부분집합의 길이를 넣는다.
  => 해당 길이를 가지는 부분집합

• 메서드에서 나왔을 때는 combinations 객체라는 형태로 있기 때문에 list 메서드로 형변환을 해주어야만 리스트로 사용할 수 있습니다.

• 공집합을 포함한 모든 부분집합을 구하려면 두번째로 들어갈 인자의 값을 배열의 길이를 모두 커버할때까지 1씩 더하면서 result 배열에 더해주면 됩니다!

시간복잡도 : O(n * nCr)

• combinations의 r(두번째 매개변수)의 값에 따라 탐색해야할 길이가 달라지기 때문에 nCr이라고 했습니다.

---

2. 단순 반복문과 배열

arr = [1, 2, 3]
subsets = [[]]

for num in arr:
  size = len(subsets)
  for y in range(size):
    subsets.append(subsets[y]+[num])
print(subsets)

• 처음에 공집합을 결과 부분집합에 넣어준다.
• 현재까지의 모든 부분집합에 첫번째 원소를 포함한 값을 추가한 배열을 부분집합에 추가한다.
• 현재까지의 모든 부분집합에 두번째 원소를 포함한 값을 추가한 배열을 부분집합에 추가한다.
• 현재까지의 모든 부분집합에 세번째 원소를 포함한 값을 추가한 배열을 부분집합에 추가한다.
• 모든원소에 대해 이 과정을 반복하면 전체부분집합이 완성된다.
• 이 부분이 말로는 이해하기 힘들 수 있으니 그림으로 설명해보겠습니다.
  

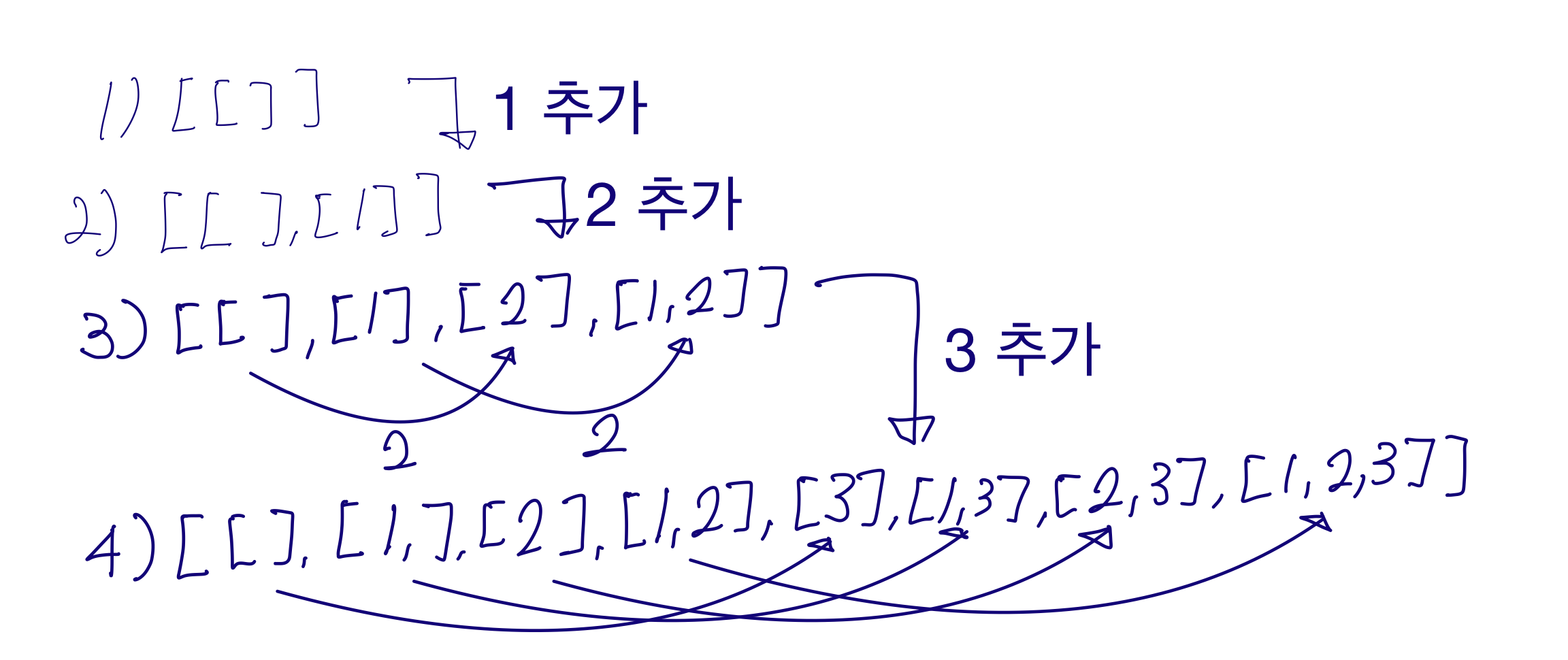
시간복잡도 : O(N * 2^N)

---

3. 재귀

import copy
result = []
def recur(subset, i, arr):	      
  if i == len(arr): 		     # 재귀함수의 탈출조건
    result.append(copy.copy(subset)) # 결과에 들어가는 모든 원소에 해당하는 부분집합의 레퍼런스가 
    return			     # subset으로 같기 때문에 subset을 카피하여 넣어줘야 한다.
				     # 이렇게 하지 않으면 result에 들어가는 모든 부분집합이 공집합으로 나온다.
  else:
    subset.append(arr[i])
    i += 1
    recur(subset, i, arr) 	     # i번째 원소가 '있을' 때의 경우에서 분화
    subset.pop()					
    recur(subset, i, arr)	     # i번째 원소가 '없을' 때의 경우에서 분화
    
recur([], 0, arr)
print(result)

• 일반적으로 모든 경우의 수를 탐색할 때는 반복문을 사용하지만, 한 가지 경우의 수에서 두 가지 이상의 상황으로 분화될 경우에는 재귀함수를 통해 탐색해야 합니다.

• 위의 그림과 같이 원소가 있는 지 각각의 인덱스의 원소가 있을 때와 없을 때의 조합을 모두 합한 것이 부분집합이 됩니다.

시간복잡도 : O(N * 2^N)

---

4. 비트연산

arr = [1,2,3] 
result = []
for i in range(1<<len(arr)): 
  subset = []
  for j in range(len(arr)): 
    if i & (1<<j): 
      subset.append(arr[j]) 
  result.append(subset)
print(result)

• 코드의 내용은 많이 다르지만 재귀함수를 통해 부분집합을 구하는 것과 완전히 같은 원리입니다.
• len(arr) => 3 이고,
• 1<<3 은 이진수 1000이 됩니다. (십진수 8)
• 첫 번째 반복문에서 각 비트 세가지가 가질 수 있는 모든 경우의 수를 사용합니다.
• 여기서 j는 각원소의 위치를 뜻합니다.

  000, 001, 010, 011, 100, 101, 110, 111

000	001	010	011	100	101	110	111
001	001	001	001	001	001	001	001
010	010	010	010	010	010	010	010
100	100	100	100	100	100	100	100
[]	[1]	[2]	[1,2]	[3]	[1,3]	[2,3]	[1,2,3]

• i & (1<<j) 은 하나라도 일치하면 0이 아니기 때문에 if 문에서 True 로 사용될 수 있습니다.

시간복잡도 : O(N * 2^N)

---

결론

• 대상이 되는 배열의 크기를 20개로 했을 때의 결과가 아래와 같습니다.

  itertools : 0.6088559627532959
  단순 반복문 : 1.1612977981567383
  재귀함수 : 1.6987059116363525
  비트연산 : 5.907625913619995

• itertools가 시간복잡도가 가장 낮았기 때문에 가장 짧은 시간이 결렸고, 나머지는 시간복잡도는 같지만 모두 다른 값이 나왔습니다.
• 비트연산이 유독 높은 이유는 빅오 표기법에 따르면 itertools를 제외한 나머지의 시간복잡도가 같지만,
• 비트연산이 실제로는 지수가 하나 더 높기 때문일 거라고 생각합니다.
• 시간복잡도가 굉장히 높기때문에 코딩테스트에서 배열의 길이가 너무 길어질 경우에는 부분집합을 구하지 않고 푸는 방법을 찾아야 할 것으로 보입니다!