자료구조(2)
6. 해시 테이블(Hash Table)
해시 테이블은 키(key)와 값(value)으로 데이터를 저장하는 자료구조이다.
해시 테이블은 검색하고자 하는 key 를 입력받아서 해시 함수를 적용하고 반환 받은 해시 코드를 배열의 인덱스로 환산을 해서 데이터에 접근한다.
원래의 데이터(key) -> Hash Function -> 반환된 결과 = Hash Code -> 배열의 Index로 사용 -> 해당 Index에 data 넣기
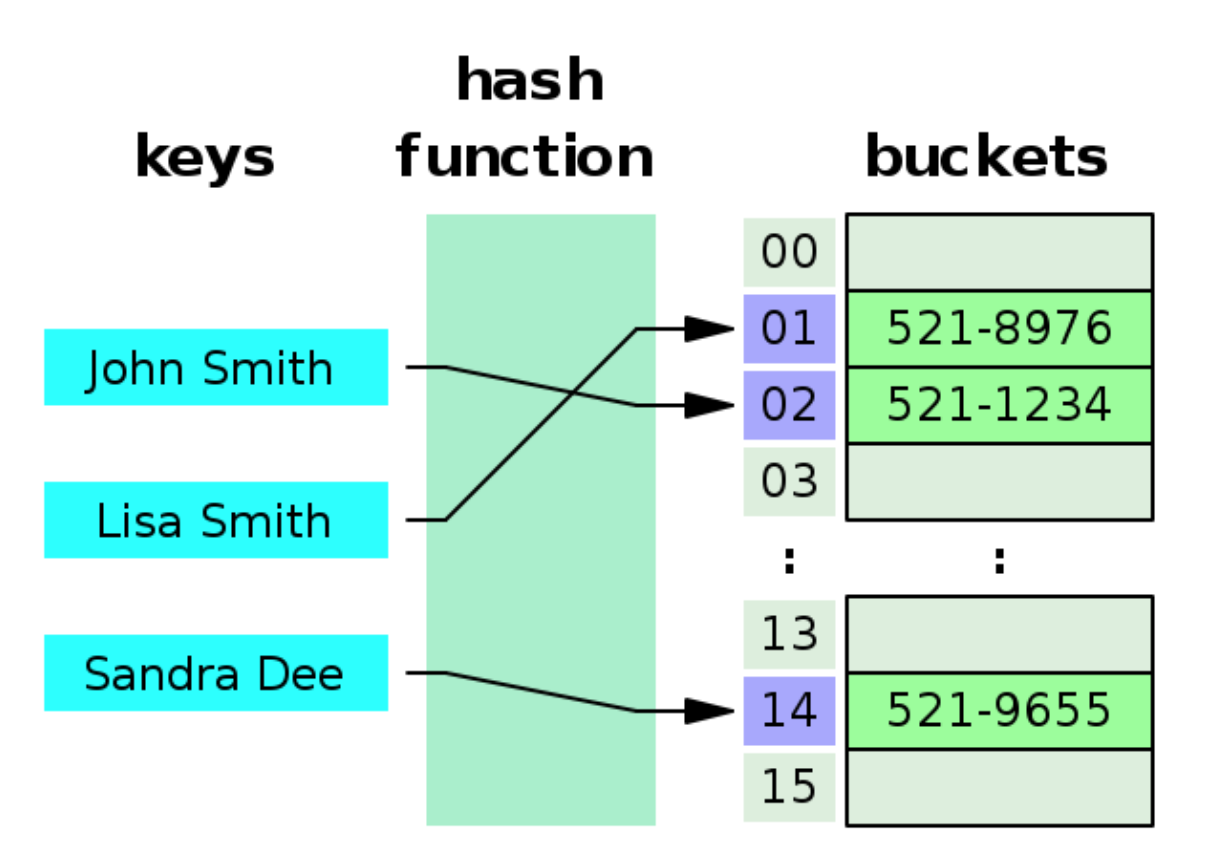[https://en.wikipedia.org/wiki/Hash_table]
John Smith 의 데이터를 저장할 때 index = hash_function("john Smith") % 16 을 통해서 index 값을 구해내고 해당 인덱스에 "john smith" 의 전화 번호를 저장한다.
hash_function 의 결과는 기본적으로 정수이기 때문에 위의 연산이 가능하다.
하지만 이런식으로 저장하다 보면 계산된 index 값이 중복이 되는 경우가 생길 수 있는데 이런 경우를 충돌(collision) 이라고 한다.
충돌(Collision)
key 값은 문자열로 무한할 수 있지만 hash code 의 값은 정수개로 중복이 될 수 밖에 없는 경우 또는 hash function 으로 서로 다른 hash code 들을 반환했지만 한정된 배열 index 로 인해서 충돌이 생기는 경우도 있다.
Separating Chaining
Linked List 를 사용하는 충돌 처리 방식이다.
[https://en.wikipedia.org/wiki/Hash_table]
시간복잡도
기본적으로 고유한 index 를 가질 경우에는 O(1) 의 시간복잡도를 가질 수 있지만 데이터의 충돌이 발생하는 경우에는 Linked List 이기 때문에 최대 O(n) 까지 증가할 수 있다.
7. 그래프(Graph)
그래프는 vertex 와 edge 로 구성된 비선형 자료구조를 의미한다. vertex 는 정점, edge 는 정점과 정점을 연결하는 간선이다.
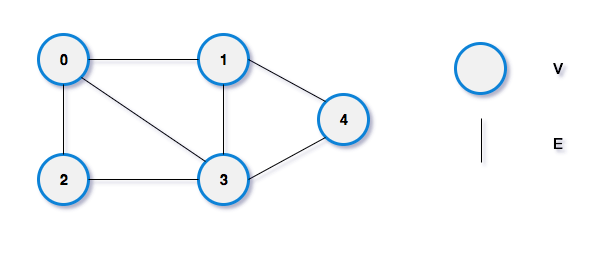[https://www.log2base2.com/data-structures/graph/graph-data-structure.html]
- 정점(vertex) : 노드라고도 하며 정점에는 데이터가 저장된다.
- 간선(edge) : 링크(arcs)라고도 하며 노드와 노드간의 관계를 나타낸다.
- 인접 정점(adjacent vertex) : 간선에 의해 직접 연결된 정점을 말한다.(위의 그림에서 0과 1 등)
- 정점의 차수(degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수 (정점 0의 차수는 3)
- 진입 차수(in-degree) : 방향 그래프에서 외부에서 오는 간선의 수
- 진출 차수(out-degree) : 방향 그래프에서 외부로 향하는 간선의 수
- 단순 경로(simple path) : 경로 중에서 반복되는 정점이 없는 경우
- 사이클(cycle) : 단순 경로의 시작 정점과 종료 정점이 동일한 경우
그래프의 종류
무방향 그래프
두 정점을 연결하는 간선에 방향이 없는 그래프
[https://www.log2base2.com/data-structures/graph/graph-data-structure.html]
방향 그래프
두 정점을 연결하는 간선에 방향이 존재하는 그래프. 간선의 방향으로만 이동이 가능하다.
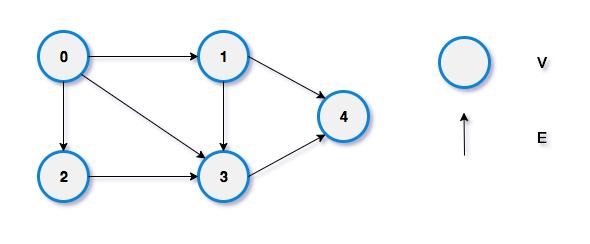[https://www.log2base2.com/data-structures/graph/graph-data-structure.html]
(0,1), (1,0) 은 서로 다르다.
가중치 그래프
두 정점을 이동할 때 비용이 드는 그래프
[https://taesan94.tistory.com/78]
완전 그래프
모든 정점이 간선으로 연결되어 있는 그래프
[https://ko.wikipedia.org/wiki/%EC%99%84%EC%A0%84_%EA%B7%B8%EB%9E%98%ED%94%84]
그래프 구현 방법
그래프를 구현하는 방법에는 인접 행렬(Adjacency Materix) 와 인접 리스트(Adjacency List) 방식이 있다.
1. 인접 행렬
정점의 수를 n, 2차원 배열 adj[n][n] 이 있을 때 i 에서 j 로 가는 간선이 있으면 1 없으면 0 으로 한다.
- 무방향 그래프
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 |
| 3 | 1 | 1 | 1 | 0 | 1 |
| 4 | 0 | 1 | 0 | 1 | 0 |
- 방향 그래프
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 0 | 0 |
1-1. 시간복잡도
노드의 수 = M, 간선의 수 = E 라고 할 때
노드 추가
노드 삭제
행과 열을 모두 추가해야 하기 때문에 노드 수의 제곱인 O(M^2) 의 시간복잡도를 가진다.
간선 추가
간선 삭제
해당하는 셀의 값만 변경(0,1)하면 되기 때문에 O(1) 의 시간복잡도를 가진다.
2. 인접 리스트
각각의 정점에 인접한 정점들을 연결 리스트로 표현한 것이다. 각 연결 리스트들은 헤더 노드를 가지고 있고 이 헤더 노드들은 하나의 배열로 구성되어 있다. 따라서 정점의 번호만 알면 이 번호를 배열의 인덱스로 하여 각 정점의 연결 리스트에 쉽게 접근이 가능하다. 리스트 내의 순서는 중요하지 않다.
- 무방향 그래프
- 방향 그래프
2-1. 시간복잡도
노드의 수 = M, 간선의 수 = E 라고 할 때
노드 추가
리스트의 끝에 추가하기 때문에 O(1) 의 시간복잡도를 가진다.
노드 삭제
노드를 삭제하면 삭제된 공간을 채우기 위해 다시 색인하는 과정이 필요하므로 노드와 정점의 개수를 합한 O(M+E) 의 시간복잡도를 가진다.
간선 추가
O(1) 의 시간복잡도를 가진다.
간선 삭제
최악의 경우 모든 Edge 를 탐색하기 때문에 최대 O(E) 의 시간복잡도를 가진다.
그래프 탐색
첫 정점에서부터 모든 정점들을 모두 한번씩 방문하는 것을 그래프 탐색이라고 한다.
그래프 탐색에는 대표적으로 깊이 우선 탐색(DFS) 방식과 너비 우선 탐색(BFS) 방식이 있다.
https://coding-factory.tistory.com/610
깊이 우선 탐색
깊이 우선 탐색은 갈 수 있는 만큼 최대한 깊이 가고 더 이상 갈 곳이 없다면 이전 정점으로 돌아가는 방식으로 순회하는 방식이다.
재귀나 스택을 사용하여 구현한다.
너비 우선 탐색
너비 우선 탐색은 시작 정점을 방문한 후 시작 정점에 인접한 모든 정점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선으로 방문하는 방법이다.
큐를 사용하여 구현한다.
8. 트리(Tree)
트리는 그래프의 일종으로 여러 노드가 한 노드를 가리킬 수 없는 구조이다.
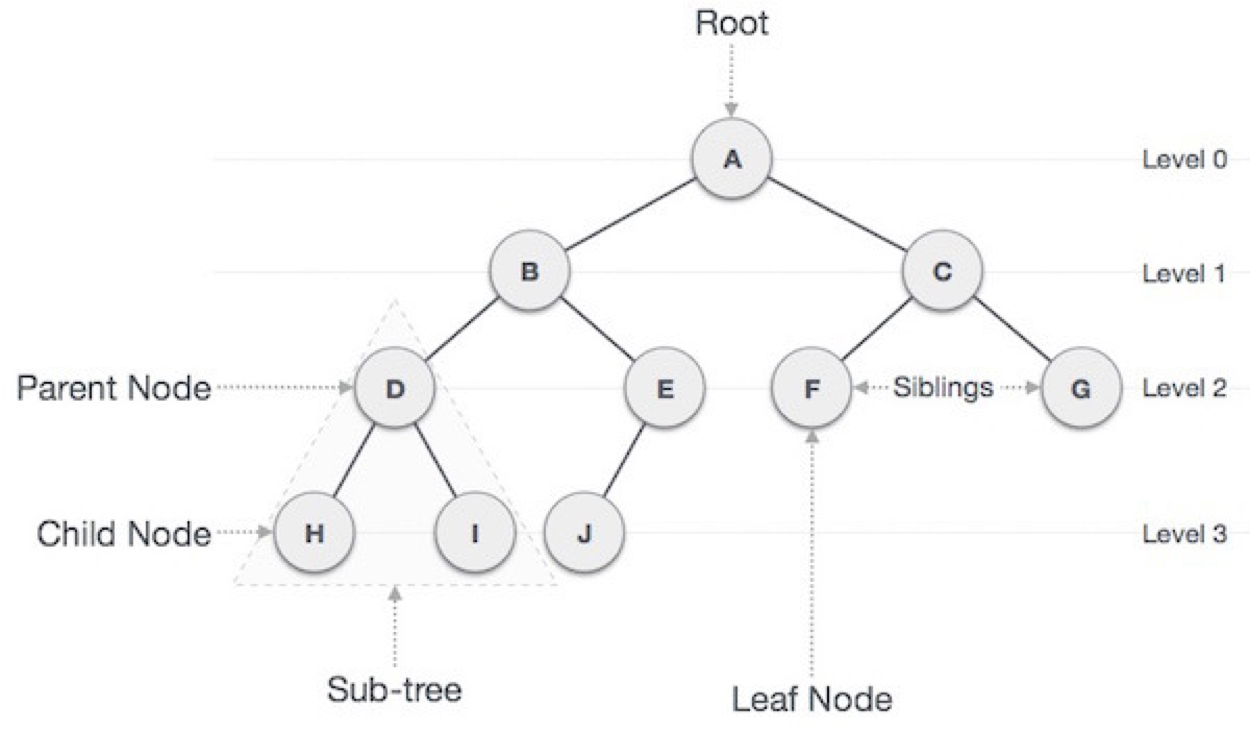
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
루트 노드(Root Node) : 트리 구조에서 최상위에 존재하는 A 와 같은 노드
노드(Node) : 트리의 구성요소에 해당하는 A,B,C,D,E,F,G,H,I,J 와 같은 요소
간선(Edge) : 노드와 노드를 연결하는 연결선
말단 노드(Leaf Node) : 제일 하단에 있는 H,I,J,F,G 와 같은 노드
Sub-Tree : 전체 트리안에 속하는 작은 트리
레벨(Level) : 트리의 특정 깊이를 가지는 노드의 집합
형제(Siblings) : 같은 부모를 가진 노드
깊이(depth) : 루트에서부터 어떤 노드에 도달하기 위해 거쳐야 할 간선의 수
높이(height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이(3)
7-1. 이진 트리(Binary Tree)
이진 트리는 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료구조이다. 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다.
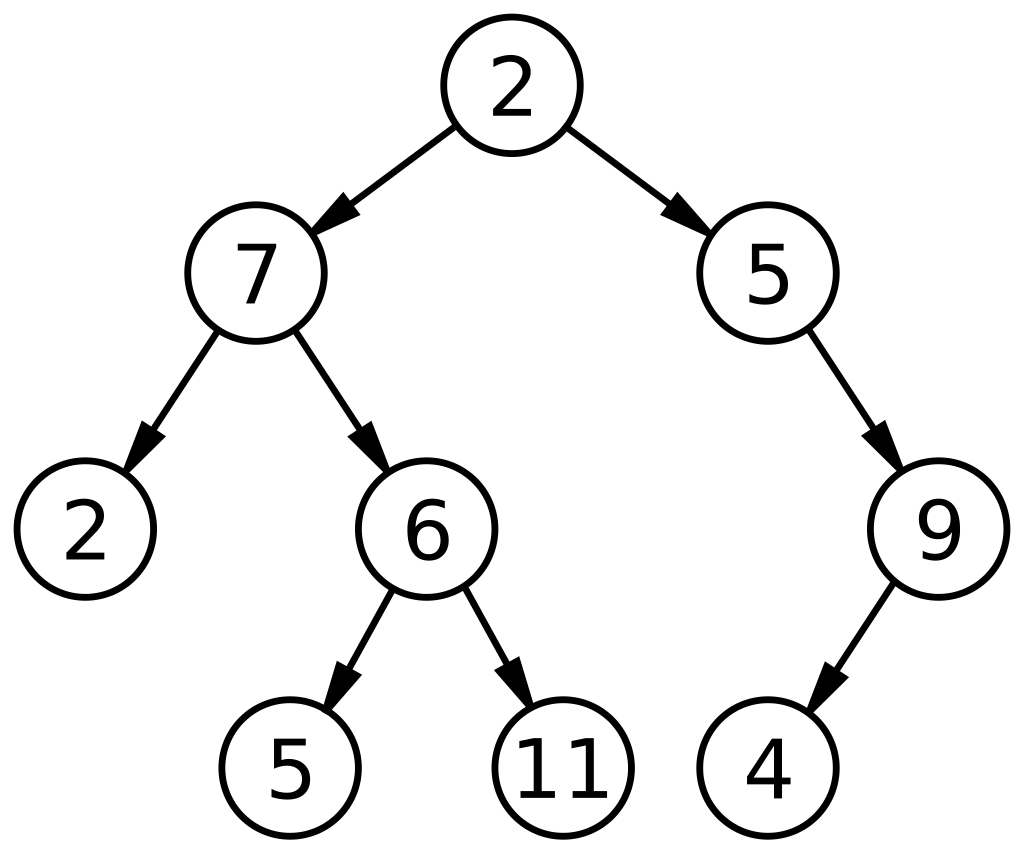
https://ko.wikipedia.org/wiki/%EC%9D%B4%EC%A7%84_%ED%8A%B8%EB%A6%AC
7-2. 완전 이진 트리(Complete Binary Tree)
완전 이진 트리란 루트부터 노드가 채워져있으면서 같은 레벨에서는 왼쪽에서 오른쪽으로 노드가 채워져있는 이진트리이다.
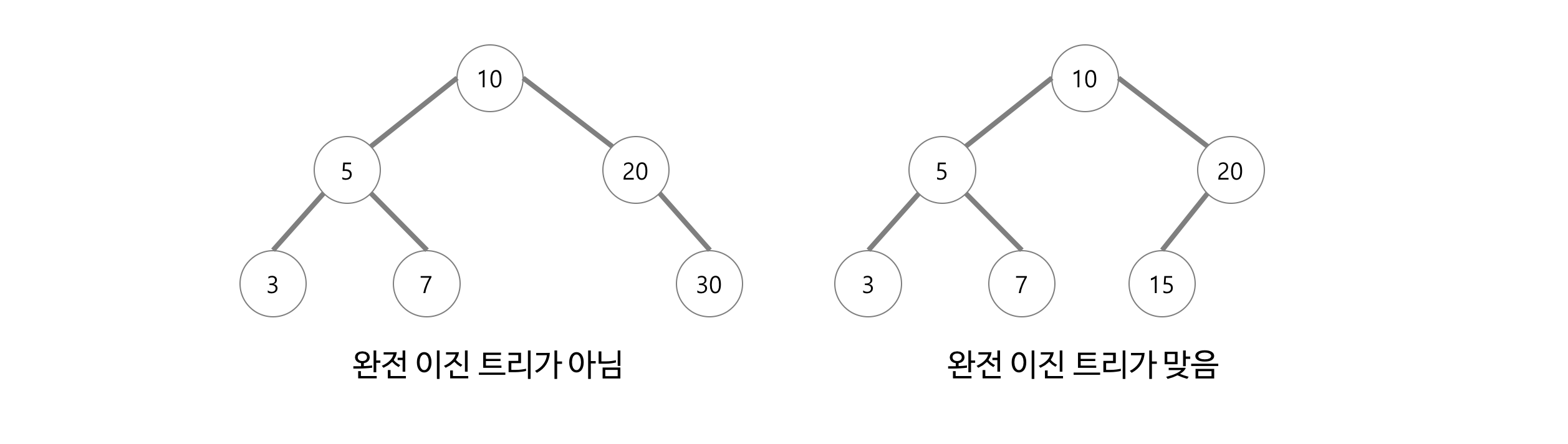
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
첫 번째 그림은 노드가 왼쪽부터 채워지지 않았기 때문에 완전 이진 트리가 아니다.
7-3. 정 이진 트리(Full Binary Tree)
정 이진 트리는 모든 노드가 0개 혹은 2개의 자식 노드를 가지는 트리를 말한다.
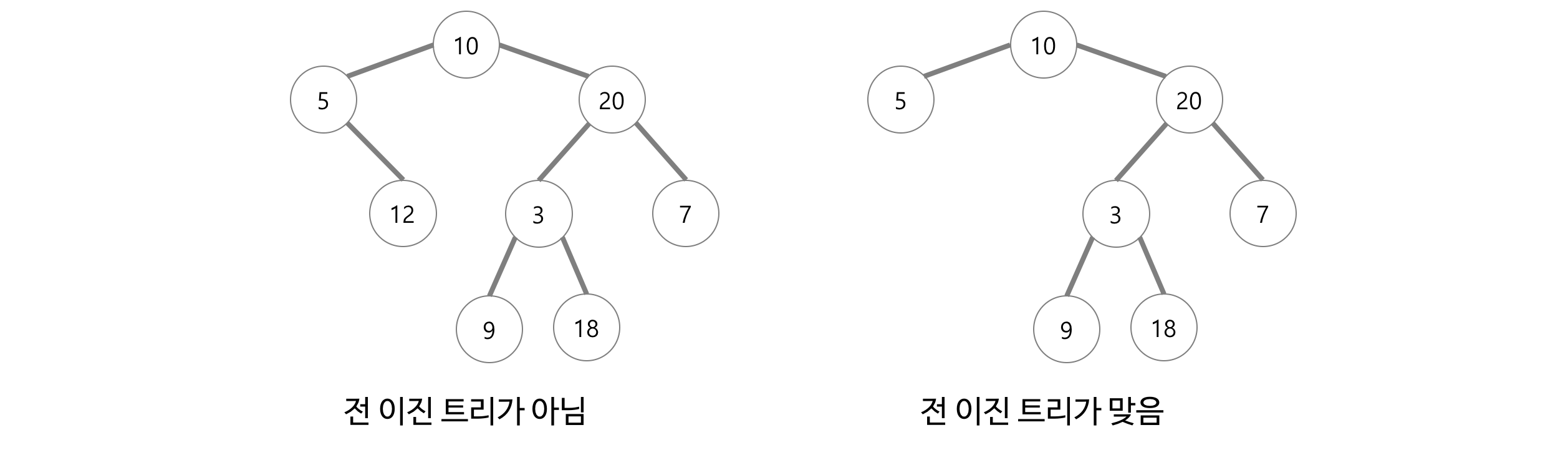
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
7-4. 포화 이진 트리(Perfect Binary Tree)
포화 이진 트리는 모든 레벨이 꽉 찬 이진 트리를 말한다. Leaf Node 가 아닌 내부 노드들은 모두 2개의 자식을 가진다.
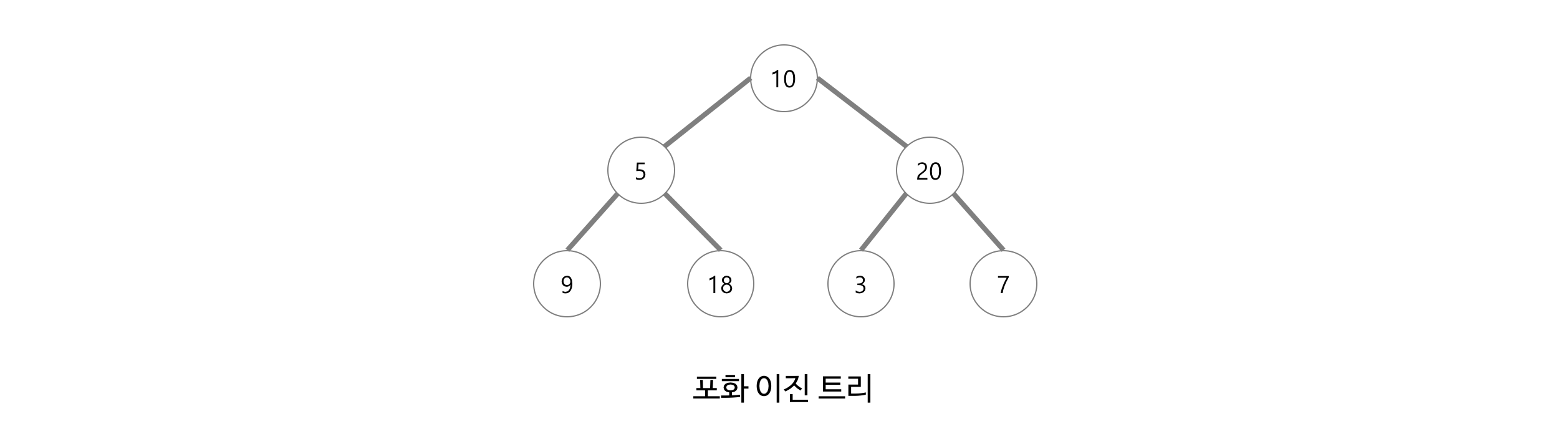
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
높이가 h인 경우 최대 노드 수는 2^(h+1)-1 이다.
7-5. 이진 탐색 트리(Binary Search Tree(BST))
이진 탐색 트리는 왼쪽 자식 노드가 부모 노드보다 작고, 오른쪽 자식 노드는 부모 노드보다 큰 트리 구조로 이진 트리 기반의 탐색을 위한 자료구조 이다.
이진 탐색 트리에서 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
https://eremo2002.tistory.com/24
탐색
위의 그림에서 4를 탐색하고 싶다면 우선 루트 노드 6과 4를 비교했을 때 4는 6의 왼쪽 서브 트리에 존재하기 때문에 오른쪽 서브 트리는 탐색할 필요가 없다.
다음으로는 왼쪽 서브 트리의 루트 노드인 2와 4를 비교하면 4가 더 크기 때문에 오른쪽 서브 트리로 내려간다.
이진 탐색 트리에서 탐색은 평균적으로는 O(logN) 의 시간복잡도를 가진다.
삽입
위의 트리에 5를 삽입해보자.
https://eremo2002.tistory.com/24
이진 탐색 트리의 삽입은 탐색을 통해 이루어지기 때문에 탐색과 마찬가지로 O(logN) 의 시간복잡도를 가진다. 삽입은 항상 Leaf Node 에서 이루어진다.
삭제
삭제 연산은 해당하는 노드를 탐색한 뒤 해당 노드를 삭제하고 이진 탐색 트리의 구조에 맞게 트리 구조를 조정하는 과정을 거친다.
삭제도 마찬가지로 O(logN) 의 시간복잡도를 가진다.
삭제 연산에는 3가지 케이스가 있다.
1.자식 노드가 없는 노드(Leaf Node)를 삭제하는 경우
해당 노드를 단순히 삭제한다.
https://eremo2002.tistory.com/24
2.자식 노드가 1개인 노드를 삭제하는 경우
해당 노드를 삭제하고 그 위치에 해당 노드의 자식 노드를 대입한다.
https://eremo2002.tistory.com/24
3.자식 노드가 2개인 노드를 삭제하는 경우
삭제하고자 하는 노드의 값을 해당 노드의 왼쪽 서브 트리에서 가장 큰 값으로 변경하거나, 오른쪽 서브 트리에서 가장 작은 값으로 변경한다.
그 다음 해당 노드를 삭제한다.
9를 삭제하는 경우를 보자.
다음은 왼쪽 서브 트리의 가장 큰 값(8) 또는 오른쪽 서브 트리의 가장 작은 값(10) 중 8을 선택할 경우이다.
8은 자식 노드가 존재하지 않기 때문에 9의 위치에 8을 위치시키고 기존 8의 위치에 있던 노드는 삭제한다.
만약 10을 선택할 경우는 어떻게 될까
https://eremo2002.tistory.com/24
9의 위치에 10을 위치시키고 10이 있던 노드는 10의 자식노드가 위치하게 된다.
이진 탐색 트리의 문제점
이진 탐색 트리의 탐색, 삽입, 삭제 연산은 평균적으로는 O(logN) 의 시간복잡도를 가지지만 만약에 다음과 같은 구조의 이진 탐색 트리라면 어떻게 될까
https://navigator-ymin.tistory.com/2
최악의 경우 모든 노드를 탐색해야 하기 때문에 O(n) 의 시간복잡도를 가진다.
이러한 문제를 해역하기 위해 자가 균형 이진 탐색 트리를 사용한다.
