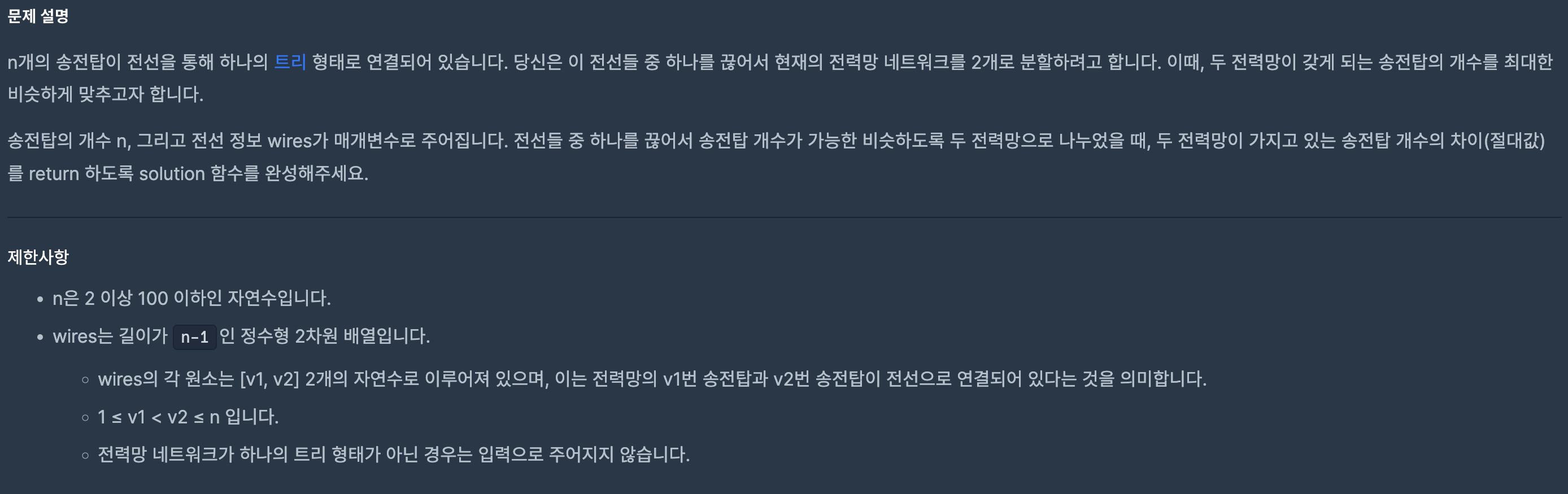
문제설명

.
이 문제는 간선한개를 임의로 지워 한 트리를 두개로 나눈 후 노드 개수 차이가 가장 적은 경우를 찾는 문제이다.
나는 이 문제를 union-find를 사용해서 풀었다.
트리에 연결된 간선을 한개씩 지우고 남은 간선들로 Union 해준 후 그렇게 나눠진 두 트리의 노드 갯수의 차이중 가장 적은 경우를 출력하게 하였다.
이 문제는 트리가 2개로만 나눠지는 탓에 부모가 1인 경우와 아닌 경우 2개로 나눌 수 있어서, union 한 후 부모가 1인 노드들의 갯수를 카운트 해주면 한 트리의 노드갯수 M이 구해진다. 나머지 다른 트리는 n - m 을 해주면 된다.
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | #include <string> #include <vector> #include <math.h> using namespace std; int parent[101]; int findpa(int a) // 부모찾기 { if (parent[a] == a) return a; return parent[a] = findpa(parent[a]); } void unionpa(int a, int b) // 결합 { a = findpa(a); b = findpa(b); if (a < b) parent[b] = a; else if (a > b) parent[a] = b; } int solution(int n, vector<vector<int> > wires) { int answer = 101; int temp = 0; // 끊을 송전탑 for (int i = 0; i < wires.size(); i++) { for (int j = 1; j <= n; j++) // 노드 초기화 { parent[j] = j; } for (int j = 0; j < wires.size(); j++) { if (j == temp) // 끊을 송전탑은 union 제외하기 continue; unionpa(wires[j][0],wires[j][1]); } int t = 0; // 갯수 세기용 임시 변수 for (int j = 1; j <= n; j++) { parent[j] = findpa(j); } for (int j = 1; j <= n; j++) { if (parent[j] == 1) t++; } answer = min(answer, abs(n - t * 2)); temp++; } return answer; } | cs |
