[백준 1004번 : 어린 왕자] java 풀이

🔔기하1 - 어린 왕자

흥미로웠던 문제...어려워보이지만 생각보다 간단하다.

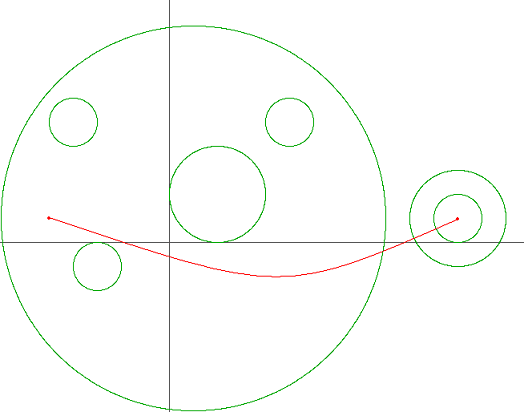
행성의 최소 진입,이탈 횟수를 구해야한다.

즉 출발점에서 도착점을 잇는 빨간 선이 원의 경계에 최소로 닿아야한다.

그림을 보면, 원이 여러 개가 있지만 출발점에서 출발할 때 출발점이 속한 큰 원 하나만 뚫고 나가면 된다.
마찬가지로, 도착점으로 도착할 때 도착점이 속한 원 2개를 뚫고 들어가야한다.

• 원의 방정식을 이용하여 출발점이 속한 원의 개수와 도착점이 속한 원의 개수를 구해야한다.

(x - a)² + (y - b)² <= r²

이때, 단순히 출발점과 도착점이 원에 속한다고 무조건 세면 안된다. 항상 반례가 있는지를 살펴야한다.

• 하나의 원 안에 출발점과 도착점이 동시에 속하면 세지 않는다.

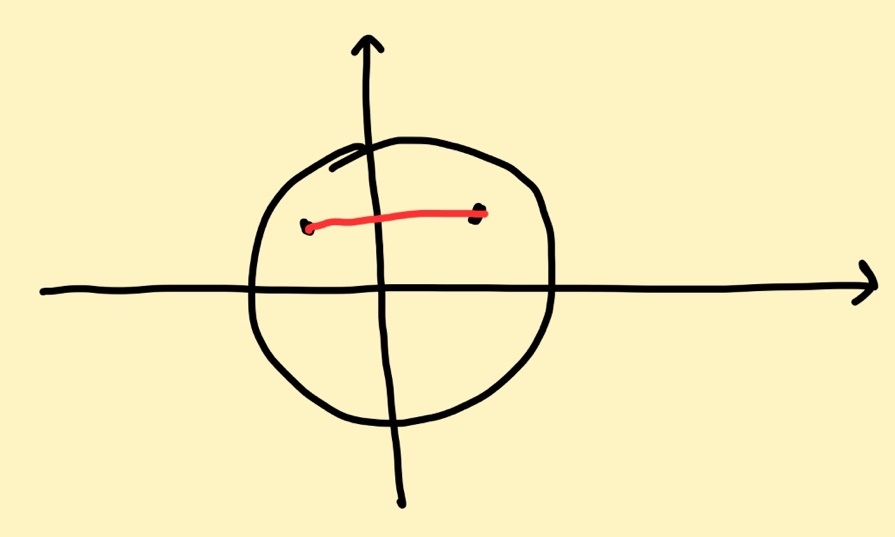
그림과 같이 한 원안에 출발점과 도착점이 동시에 있으면 최소 진입,이탈 횟수는 0이되므로 세면 안된다. 이 점을 유의해야한다.

🔑 java 풀이

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main{
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		int T = Integer.parseInt(br.readLine());
		int start[] = new int[2];//출발점 입력
		int end[] = new int[2];//도착점 입력
		int circle[]=new int[3];//원 입력
		
		for(int i=0; i<T; i++) {
			StringTokenizer st = new StringTokenizer(br.readLine()," ");
			start[0]=Integer.parseInt(st.nextToken());//출발 x
			start[1]=Integer.parseInt(st.nextToken());//출발 y
			end[0]=Integer.parseInt(st.nextToken());//도착 x
			end[1]=Integer.parseInt(st.nextToken());//도착 y
			int n=Integer.parseInt(br.readLine());
			int cnt=0;//최소의 행성계 진입,이탈 횟수
			for(int j=0; j<n; j++) {
				boolean startPoint=false;
				boolean endPoint=false;
				st=new StringTokenizer(br.readLine()," ");
				circle[0]=Integer.parseInt(st.nextToken());//원 중심 x
				circle[1]=Integer.parseInt(st.nextToken());//원 중심 y
				circle[2]=Integer.parseInt(st.nextToken());//원의 반지름
				//(x-a)^2 + (y-b)^2 <= r^2
				//출발점, 도착점이 행성계(원) 안에 있는지를 판단함
				if(Math.pow(start[0]-circle[0], 2)+Math.pow(start[1]-circle[1], 2)<=Math.pow(circle[2], 2)) {
					startPoint=true;
					cnt++;
				}
				if(Math.pow(end[0]-circle[0], 2)+Math.pow(end[1]-circle[1], 2)<=Math.pow(circle[2], 2)) {
					endPoint=true;
					cnt++;
				}
                //한 원안에 출발점,도착점이 동시에 속하면 cnt증가를 취소함
				if(startPoint==true && endPoint==true)
					cnt-=2;
			}
			sb.append(cnt+"\n");
		}
		System.out.print(sb);
		br.close();
	}
}