[백준] 알고리즘

우선 원판 이동의 최소 횟수 값을 출력해야한다. 해결 방법은 두 가지가 있다.재귀함수로 (n-1)\*2+1 값을 return 한다.참고로 (n-1)\*2+1 값이 최소 횟수는 아니다. 여기서 말하는 (n-1)은 n-1개의 원판을 옮기는 최소 횟수를 말한다.따라서 (n-

복잡하게 생각하지 않고 최대한 단순하게 풀었다.첫번째 i를 정하고, 그 다음부터는 j, 그 다음은 z 순으로 반복문을 이용하여 정렬하듯이 최대합을 갖는 카드 3개의 조합을 찾아나갔다.

주어진 자연수 N이 최대 1000000까지이므로 이를 고려하여 각 자릿수를 구하는 함수를 작성했다.분해합은 자신과 분해된 자릿수들의 합이므로 어차피 생성자는 주어진 분해합인 N보다 작을 수 밖에 없다.따라서 1부터 N미만까지 차례대로 생성자가 될 수 있을지 대조했을

각 사람끼리 키와 몸무게를 한번씩 다 돌아가면서 매칭하여 비교하고 자신보다 덩치가 큰 사람의 수를 세는 간단한 문제이다.

간단하지만 생각보다 헤매느라 시간을 잡아먹은 문제...특히 자바는 익숙하지 않아서 scanner를 사용하지않고 받는 부분에서 약간 헷갈렸다.요약하자면,B로 시작하는 88체스판과 W로 시작하는 88체스판 두 개의 배열을 준비함.첫 시작 좌표를 (i , j)로 잡는다.시작

숫자를 문자열로 변환한 후 그 문자열에 "666"이 포함되어 있는지를 검사만하면 된다. 반복문은 쉽게 While(true)를 이용하였다.자바에서 숫자를 문자열로 변환하는 방법String s = Integer.toSring(i);String s = String.value

백준 정렬 문제 중 가장 기초적인 문제이다. 🔔문제 설명란을 보면시간 복잡도가 O(n²)인 정렬 알고리즘으로 풀 수 있습니다. 예를 들면 삽입 정렬, 거품 정렬 등이 있습니다.고민도 안하고 선택정렬을 이용했다.

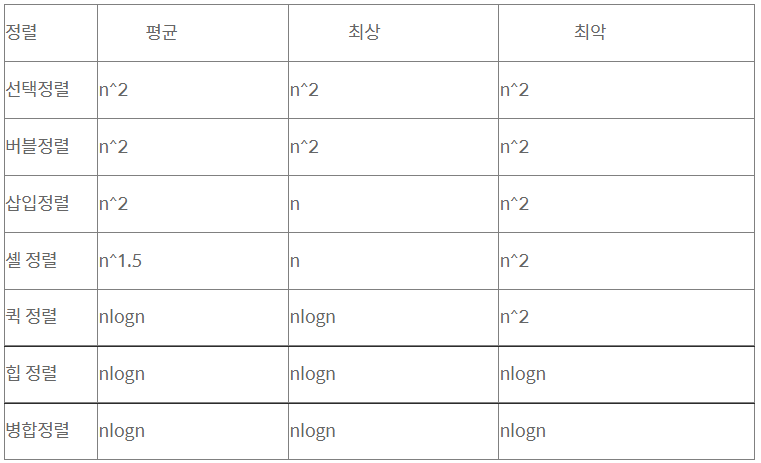
"시간 복잡도가 O(nlogn)인 정렬 알고리즘으로 풀 수 있습니다. 예를 들면 병합 정렬, 힙 정렬 등이 있지만, 어려운 알고리즘이므로 지금은 언어에 내장된 정렬 함수를 쓰는 것을 추천드립니다."병합 정렬, 힙 정렬은 나중에 공부하고 지금은 설명란의 추천대로 자바 안

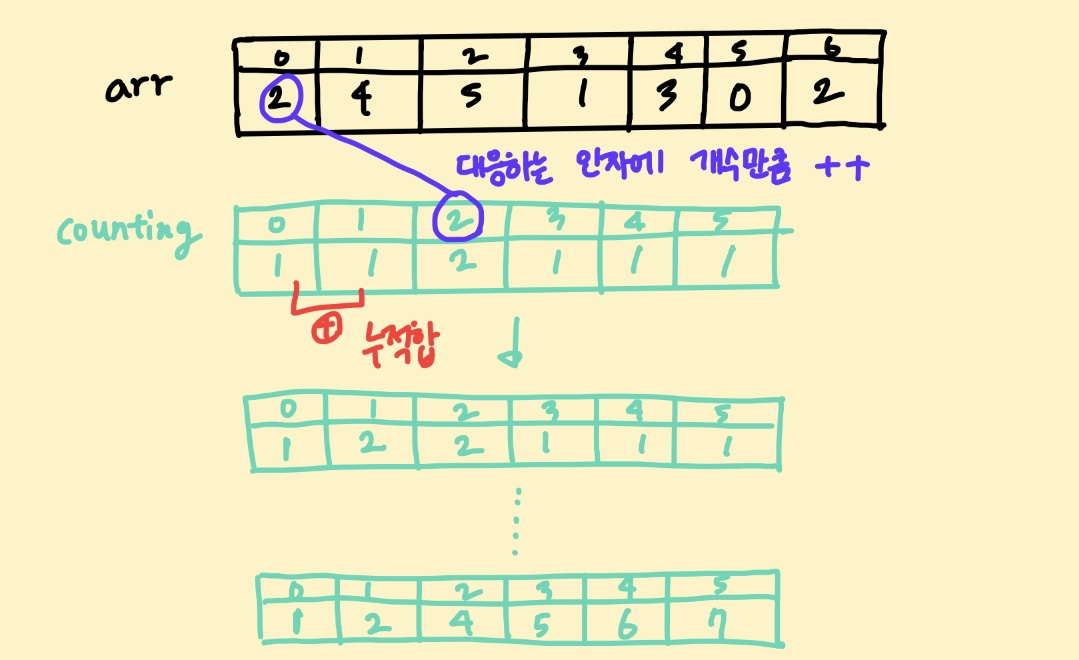
"수의 범위가 작다면 카운팅 정렬을 사용하여 더욱 빠르게 정렬할 수 있습니다."문제 힌트대로 카운팅 정렬을 이용해서 풀어보았다.\*카운팅 정렬 : 각 항목이 몇 개씩 있는지 세어서 정렬하는 알고리즘으로 시간복잡도 O(n)으로 굉장히 빠르다.ㅎㅎ발그림으로 설명해보았다.인

쉽다고 생각했는데 생각보다 헤맸던 문제...상대적으로 평균값, 중앙값, 범위는 구하기 매우 쉬웠다.처음에 풀 때는 최빈값에서 정렬을 여러번 썼다. 풀면서도 너무 코드가 복잡해지고 느낌이 불길했는데 역시나 시간초과가 떴다...그래서 선택한 방법은 카운팅 정렬이다.최빈값의

상대적으로 굉장히 쉬운 문제로 문자열을 잘 다뤄야한다.입력받은 수를 String으로 변환String을 char 배열로 변환아스키코드 값을 이용해서 문자값을 간단히 숫자로 변환Arrays.sort로 오름차순 정렬 후 역방향으로 출력업로드중..

람다식을 이용하여 해결하는 문제 람다식을 모를 때 선택정렬을 이용하여 풀었다가 시간초과가 돼버렸다... 결국 인터넷을 검색해서 풀 수 밖에 없었다. 이 문제를 자바로 풀 때는 람다식을 이용하여 Arrays.sort를 확장하는 방법을 사용한다. 참고링크 : http

이전 문제인 <11650번 : 좌표 정렬하기> 와 거의 비슷한 문제이다.바뀐 건 y좌표를 우선으로 정렬하고, y좌표가 같으면 x좌표를 정렬하는 것이다.따라서 특별한 설명은 필요없을듯..

처음에 Arrays.sort()를 확장하여 풀려고 시도했으나 이해가 부족했는지 실패하고 결국 선택정렬을 이용해서 풀어냈다.인터넷 검색을 통해서 풀이를 봤더니 Arrays.sort()의 compare 메소드를 이해할 수 있었다.int 배열을 Arrays.sort로 정렬할

이 문제는 생성자로 객체 배열을 생성하여 Arrays.sort로 풀어낸다. Main 클래스는 나이(age), 이름(name)의 멤버 필드를 갖는다. 생성자를 호출해서 Main 타입의 객체 배열에 사용자 정보를 담는다. 나이순으로 정렬하도록 Arrays.sort의 co

결과는 계속 맞는데 시간초과때문에 미치게 만든 문제였다.무수한 시간초과의 수집 우하하일단 문제를 푸는 기본 구조는,arr에 x좌표를 입력받는다.arr을 똑같이 복사한 sort를 만들고 sort를 정렬한다.arr에서 x좌표 순서대로 sort에서의 해당 좌표의 인덱스를 출

집합을 이용한 문제이다.집합의 성질원소는 중복되지 않는다.순서는 있을 수 있다.정렬이 가능하다.쉽게 풀 수 있는 문제이다. 단순히 집합에 N개의 숫자카드를 넣고 M개의 숫자카드와 비교하여 포함되어있으면 배열에 1을, 없으면 0을 넣는다.

이전 문제인 숫자카드와 거의 유사한 문제이다. 시간초과를 방지하기 위해 BufferedReader를 사용했다.

해쉬맵을 이용하여 숫자와 문자열을 연결했다. 처음에는 (인덱스, 문자열)로만 맵에 넣었더니 문자열을 입력받을 때 인덱스 값을 가져오지 못해 반복문을 사용했더니 시간초과가 났다. (인덱스, 문자열)과 (문자열, 인덱스)를 동시에 맵에 넣음으로써 해결했다.포켓몬 스토리 읽

이 문제는 <집합과 맵> 단계라서 보통 맵을 이용하여 푼다. 맵을 이용할 경우HashMap을 이용하여 Key값에 숫자카드를 N개만큼 넣는다.이 때 getOrDefault를 이용해 중복값이 있으면 value를 증가시킨다.M개 만큼 입력받은 숫자카드를 키값에 넣어 해

이 문제는 집합의 교집합을 이용해야한다.집합 HashSetaddAll() 합집합retainAll() 교집합removeAll() 차집합containsAll() 부분집합 포함 여부푸는 과정은,듣도 못한 사람 집합과 보도 못한 사람 집합의 교집합을 구한다.HashSet을 A

(A-B)와 (B-A)의 합집합을 구해야한다.이 때 A집합의 B차집합을 하면 A집합에는 (A-B)가 들어가므로 따로 A집합 복사한 집합을 선언해야한다.

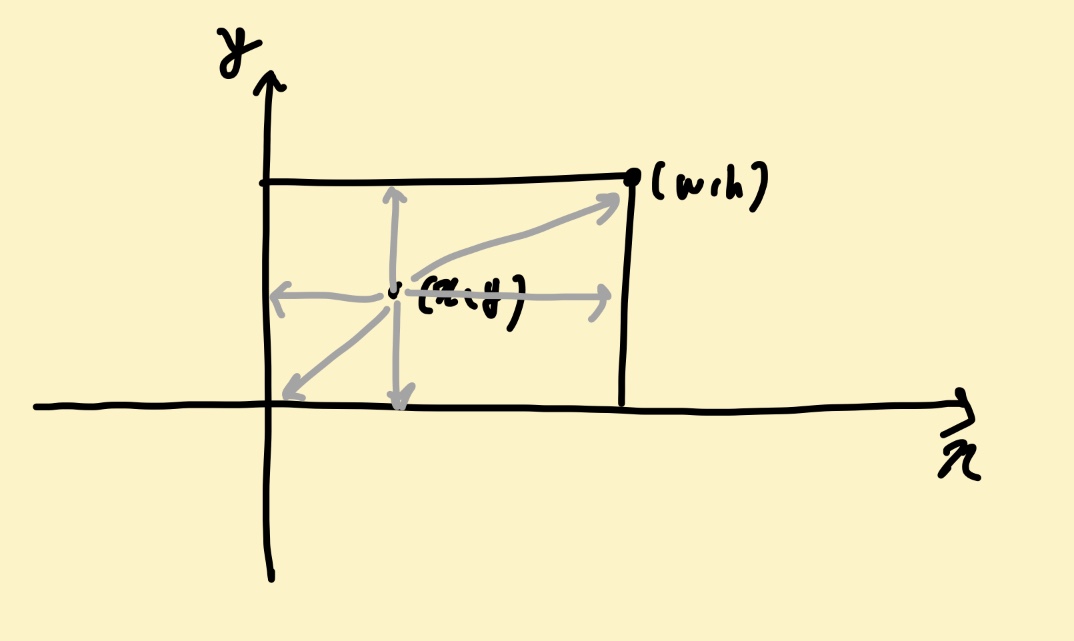
오랜만에 수학 문제 푸는듯한 기분이 들었다...사실 수학문제라고 하기도 민망할정도로 간단하게 풀 수 있다.점 (x , y) 가 직사각형까지 최소값이 될 수 있는 거리의 경우를 모두 생각해야한다.점 (x , y)는 직사각형 안에 있다. (1 ≤ x ≤ w-1, 1 ≤ y

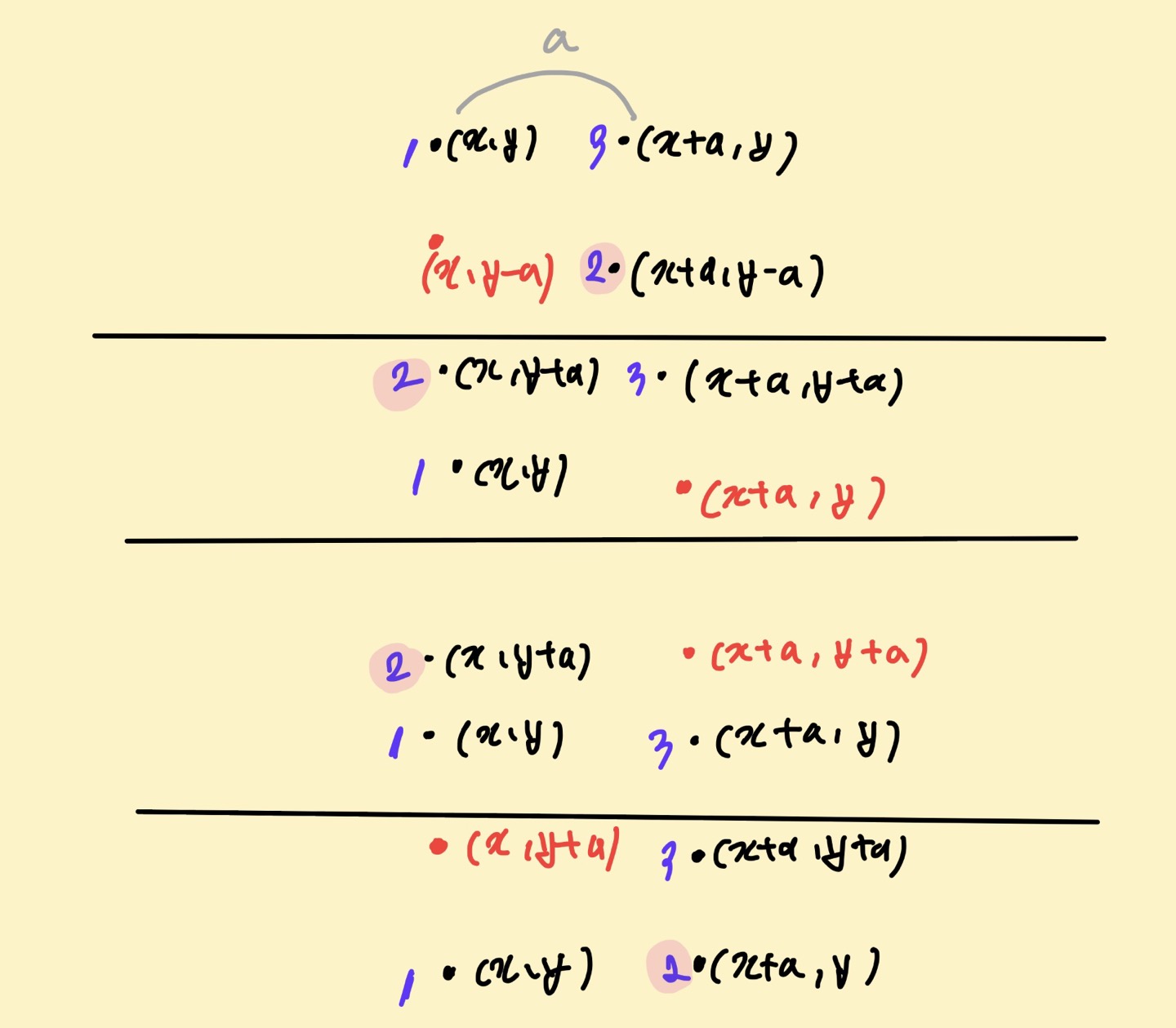
이 문제는 약간의 생각을 하게 만든 문제..이런 문제를 풀 때는 노트나 아이패드에 그림을 그려보는 것이 좋다.내가 문제에 접근한 방식을 정리하자면,우선 직사각형의 한 변을 a라고 정의하였다.입력받은 3개의 점을 x좌표 순서대로 먼저 정렬하고, x좌표가 같으면 y좌표 순

🔔기하1 - 직각삼각형 피타고라스 정리만 안다면 굉장히 쉬운 문제이다.. while 문을 이용하면 된다. 참고로 예제 입력은 변의 길이 순서대로였지만, 문제에서 특별히 변의 길이 순서대로 입력하라는 말이 없다. >즉 순서대로 입력을 안 할수도 있음을 주의해야한다.

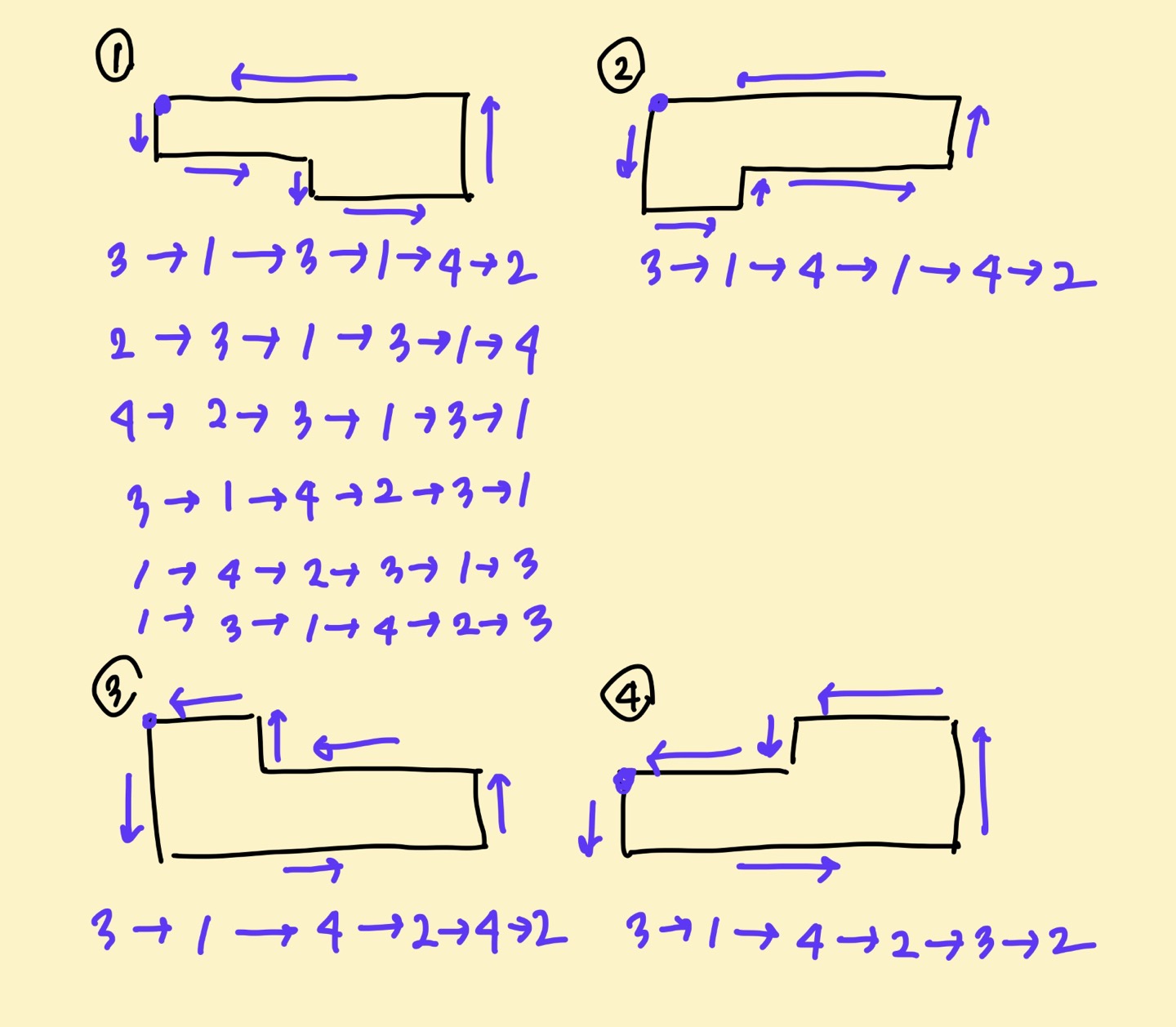
생각보다 푸는데 시간이 걸린 문제...실수를 많이 했다.문제에서는 임의의 한 꼭짓점에서 출발하게한다. 이럴 경우 꼭짓점마다 변의 방향 순서가 달라지므로 따져야할 케이스가 너무 많아진다. 따라서 왼쪽 위 꼭짓점에서 시작하도록 입력받은 변의 방향 순서를 돌리는 것이 중요하

유클리드 기하학과 택시 기하학에서의 원의 넓이는 차이가 있다.간단하게 정리하면 좌표평면상에서 유클리드의 원은 우리가 아는 흔한 원이다. 하지만 택시 기하학에서의 원은 정사각형 모양이 45도로 기울어진 모양이다.그 원리는 인터넷에서 직접 검색해보는 것이 좋다...유클리드

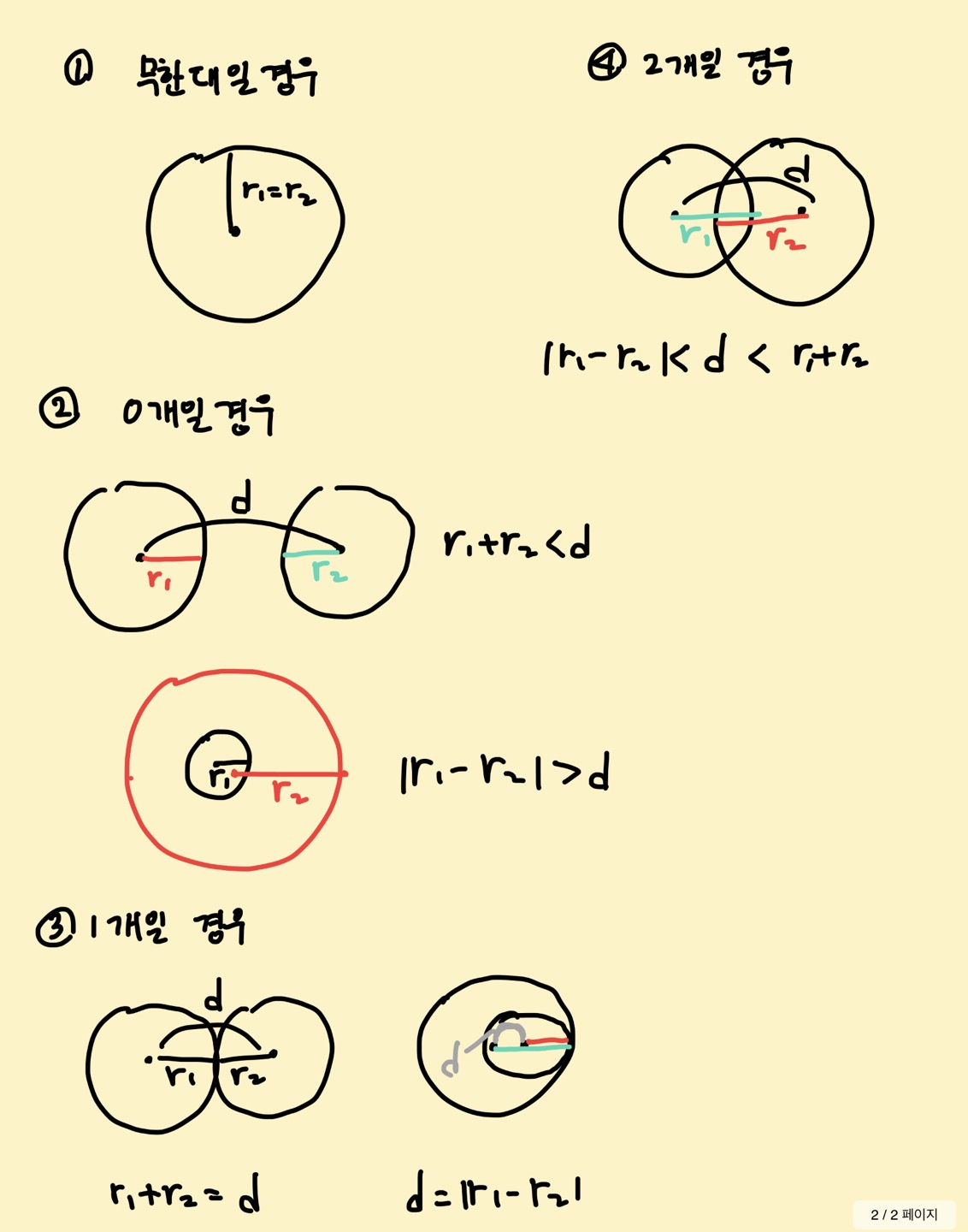
고등학교 시절로 돌아간 기분...중심점 사이의 거리와 반지름으로 두 원과의 교점 개수를 구한다.1) 원의 중심점이 같을 경우반지름이 다른 경우 : 0개반지름이 같은 경우 : 무한대2) 원의 중심점이 다를 경우원이 외부에서 떨어져 있을 경우 : 한 원이 다른 원 안에 있

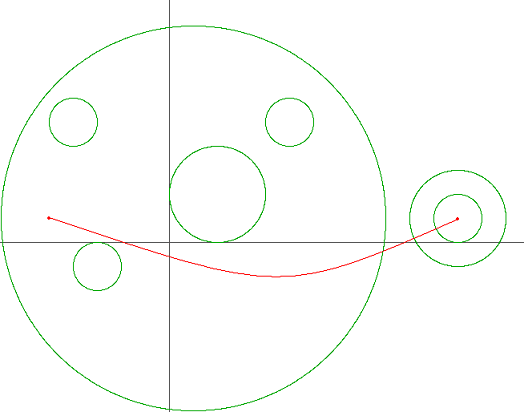
흥미로웠던 문제...어려워보이지만 생각보다 간단하다.행성의 최소 진입,이탈 횟수를 구해야한다. 즉 출발점에서 도착점을 잇는 빨간 선이 원의 경계에 최소로 닿아야한다.그림을 보면, 원이 여러 개가 있지만 출발점에서 출발할 때 출발점이 속한 큰 원 하나만 뚫고 나가면 된다

동적계획법 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 쉽게 말하면 답을 재활용한다고 볼 수 있다. > 동적계획법(DP)은 점화식을 구하는 것이 중요하다. 점화식을 구해서 재귀적인 방법으로 풀거나 반복문을 이용하여 풀 수 있다.

연속적인 합의 크기를 구하는 문제이므로 dp 배열에 연속합의 결과를 담아야한다.우선 arr 배열에 임의의 수열을 저장한다.dp 배열에 인덱스 n까지의 합을 저장한다.이 때 (인덱스 n-1까지의 합) + arrn 과 arrn 중 큰 값을 dp에 저장한다.즉 이전까지의 합

굉장히 쉬운 문제로 동적계획법을 이해할 수 있는 기초 문제이다.피보나치 수를 재귀함수와 반복문으로 구현하면 된다.

이 문제는 나에게 고통을 줬어.. 생각보다 간단한 문제인데 굉장히 헤맸던 거 같다. 처음 풀었던 방법은 이랬다. 1번 집에 최소 비용을 가지는 색을 칠한다 그 다음 집은 1번 집에 칠한 색을 제외하고 최소 비용을 가지는 색을 칠한다. 이렇게 풀었는데 잘못된 접근 방

Temp Body

백준 2579번 : 계단 오르기 바로가기이 문제는 또 굉장히 헷갈렸다..(나 진짜 바보인가😭)단계별 알고리즘 문제는 각 문제마다 백준에서 작은 힌트를 코멘트로 달아놓는다. 이를 확인해보면,"i번째일 경우, 몇 개의 연속한 계단을 올랐는지 고려하라"즉 점화식을 세울 때

1463번 : 1로 만들기 문제 링크우리가 사용할 수 있는 연산은 총 3가지이다.여기서 3번의 경우는 모든 1을 제외한 모든 정수에 사용할 수 있다.하지만 1번과 2번은 모든 정수에 사용할 수는 없다. 따라서 우리는 조건문을 이용하여 경우를 따져야한다.1) 3과 2 모

백준 2156번 : 포도주 시식 문제 링크계단 오르기와 굉장히 유사한 문제로써 차이점만 주의하면 된다.계단 오르기는 마지막 값이 꼭 포함되어야한다.하지만 이 문제는 마지막 값이 꼭 포함될 필요가 없다.규칙에 의하면, 연속 3잔을 마실 수 없다. 이 부분이 계단 오르기와

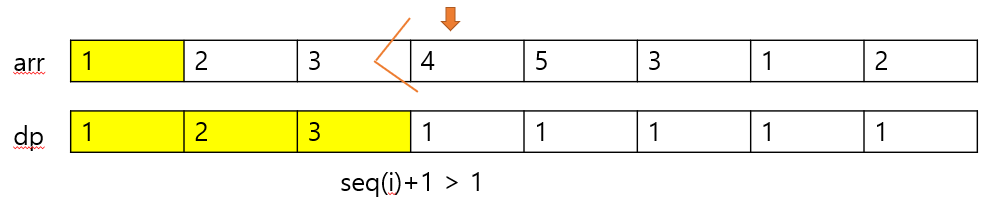
발그림으로 설명해봤당n번째 인덱스까지의 가장 긴 수열을 구한다고 했을 때 n-1번째까지를 따져야한다. 만약 n번째 숫자가 0번째~n-1번째 까지 순환한다고 하면 순환하는 각 숫자는 i번째 인덱스라고 지칭한다. 각 i번째 숫자보다 n번째 숫자가 클 경우 해당 숫자의 dp

선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법그리디 알고리즘의 해결 과정선택 절차: 현재 상태에서의 최적의 해답을 선택한다.적절성 검사: 선택된 해가 문제의 조건을 만족하는지 검사한다.해답 검사: 최적해가 아니면 이전 절차로 돌

dp는 너무 어렵다. 쉬운 난이도이지만 한참 생각하고 헤맸다..dp에서 중요한 것은 가장 먼저 dpi가 무엇인지 정의하고 점화식을 찾는 것이다.dpi = i번째 날까지 최대 수익이라고 하자.우선 i+ti-1이 n을 초과하면 그 상담은 진행할 수 없다.N+1일째에는 회사

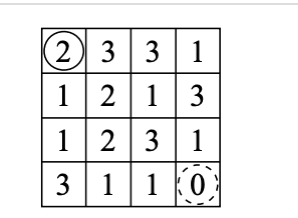
메모리를 사용하기 위해 게임판과 똑같은 모양의 dpn 배열 생성dpi = 해당 위치까지 올 수 있는 경로의 수라고 정의함직접 예제 입력1 케이스를 그려보면서 패턴을 찾음차례대로 dp배열을 순회하며 dpi값이 0이 아닌 경우 경로 누적 수행.(dpi값이 0인 경우는 해당

dpi = 합이 i일 때 끝이 1로 끝나는 경우의 수dpi = 합이 i일 때 끝이 2로 끝나는 경우의 수dpi = 합이 i일 때 끝이 3으로 끝나는 경우의 수dp1 = 1(1)dp2 = 1(1+1)dp2 = 1(2)dp3 = 1(1+1+1)dp3 = 1(1+2)dp3