[백준 2156번 : 포도주 시식] java풀이

백준 2156번 : 포도주 시식 문제 링크

계단 오르기와 굉장히 유사한 문제로써 차이점만 주의하면 된다.

계단 오르기는 마지막 값이 꼭 포함되어야한다.
하지만 이 문제는 마지막 값이 꼭 포함될 필요가 없다.

규칙에 의하면, 연속 3잔을 마실 수 없다. 이 부분이 계단 오르기와 굉장히 유사하다.

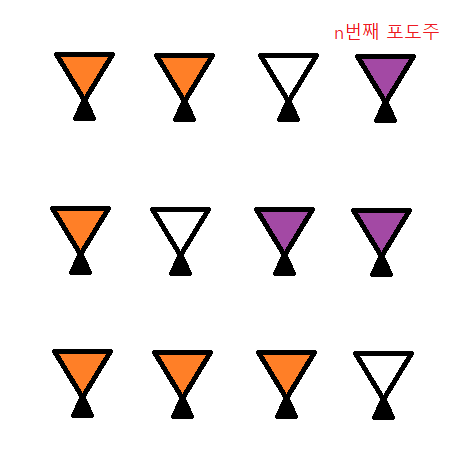
열심히 그림판으로 그려보았다..ㅎㅎ
3잔이 연속으로 비워질 수 없는 걸 고려해야 한다.

보라색 잔은 무조건 마시므로 합하고, 주황색 잔은 재귀함수로 탐색해야하는 부분, 빈 잔은 마시지 않아 합하지 않는 부분이다.

첫번째 그림 : n번째 포도주를 마시고 n-1번째는 마시지 않고 n-2번째부터 재귀함수를 호출하여 dp 값을 탐색한다.

두번째 그림 : n번째 포도주를 마시고 n-1번째도 마시고, n-2번째는 마시지 못하고 n-3번째부터 재귀함수를 호출하여 dp 값을 탐색한다.

세번째 그림 : 마지막 잔을 포함하지 않고 n-1번째 잔부터 탐색한다.

따라서 점화식은 다음과 같다.
Max(grape(n-2)+wine[n], grape(n-3) + wine[n-1]+ wine[n], grape(n-1));

🔑java 풀이

import java.io.IOException;
import java.util.Scanner;

public class Main {
    static int dp[];
    static int wine[];
    static int N;
    static int grape(int n){
        if(dp[n]==-1){
            dp[n] = Math.max(Math.max(grape(n-2), grape(n-3) + wine[n - 1]) + wine[n],grape(n-1));
        }
        return dp[n];
    }

    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        N = sc.nextInt();
        wine=new int[N+1];
        for(int i=1; i<N+1; i++){
            wine[i]=sc.nextInt();
        }

        dp=new int[N+1];
        for(int i=1; i<N+1; i++)
            dp[i]=-1;
        dp[1]=wine[1];
        if(N==1){
            System.out.println(dp[1]);
            return;
        }
        if(N>1){
            dp[2]=wine[1]+wine[2];
        }
        if(N==2){
            System.out.println(dp[2]);
            return;
        }

        System.out.println(grape(N));

    }
}