[Data Structure] 그래프 (Graph)

Sieun·2023년 1월 6일

algorithm data structure

Algorithm

목록 보기

6/8

그래프(Graph)란?

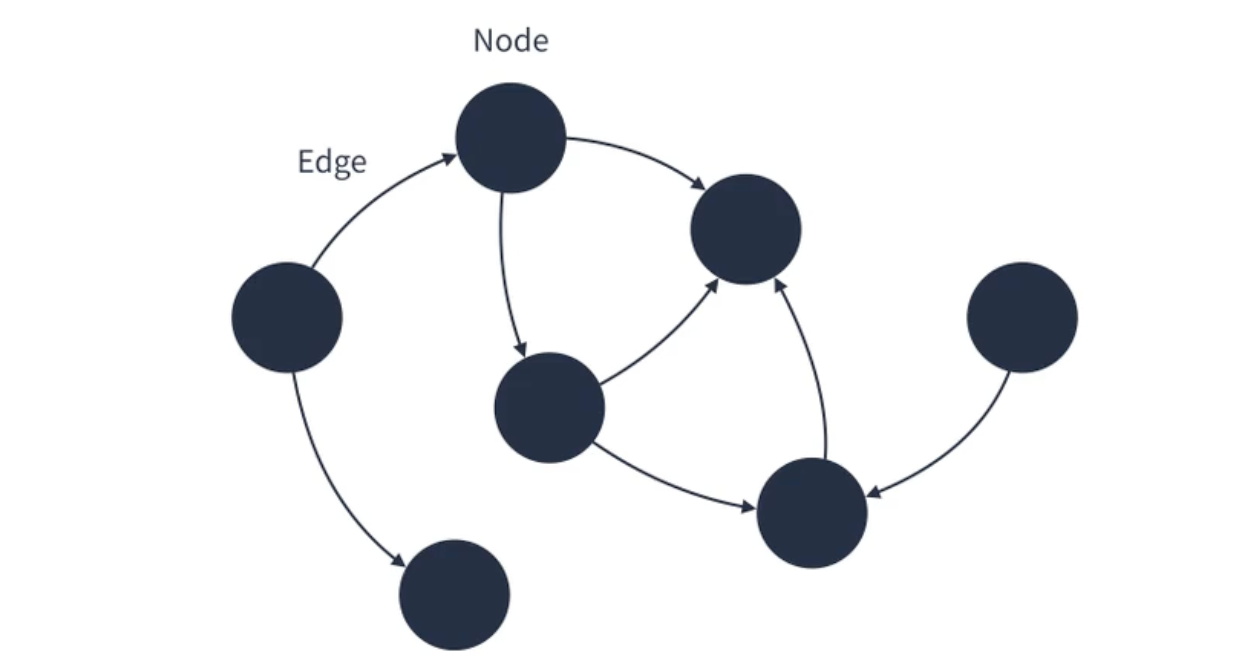
그래프(Graph) 는 정점과 정점 사이를 연결하는 간선으로 이루어진 비선형 자료구조다. 정점 집합과 간선 집합으로 표현할 수 있다.

그래프(Graph)

정점 (vertex) : 노드(node)라고도 하며 데이터가 저장되는 그래프의 기본 원소다.
간선 (edge) : 정점 간의 관계를 나타낸다. (정점을 이어주는 선)
인접 정점 (adjacent vertex) : 하나의 정점에서 간선에 의해 직접 연결된 정점을 뜻한다.
가중치 그래프 (weighted Graph) : 연결의 강도(추가적인 정보, ex. 서울-부산으로 가는 거리 등)가 얼마나 되는지 적혀져 있는 그래프를 뜻한다.
진입차수 (in-degree) / 진출차수 (out-degree) : 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타낸다.
인접 (adjacency) : 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점이다.
자기 루프 (self loop) : 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다 라고 표현한다. 다른 정점을 거치지 않는다는 것이 특징이다.
가중치 : 간선 위에 표시된 숫자다. 가중치는 필수가 아니라 없는 것도 있어, 가중치가 없는 그래프는 모두 동일한 가중치를 가지고 있다. 해당 간선을 타고 이동할 때 필요한 비용 등을 표현하는 것에 사용된다.
비 가중치 그래프 (unweighted Graph) : 연결의 강도가 적혀져 있지 않는 그래프를 뜻한다.

그래프의 특징

정점은 여러 개의 간선을 가질 수 있다.
크게 방향 그래프와 무방향 그래프로 나눌 수 있다.
간선은 가중치를 가질 수 있다.
사이클이 발생할 수 있다.
사이클 (Cycle) : 그래프의 정점과 간선의 부분 집합에서 순환이 되는 부분(영역)이다.

사이클

그래프의 종류

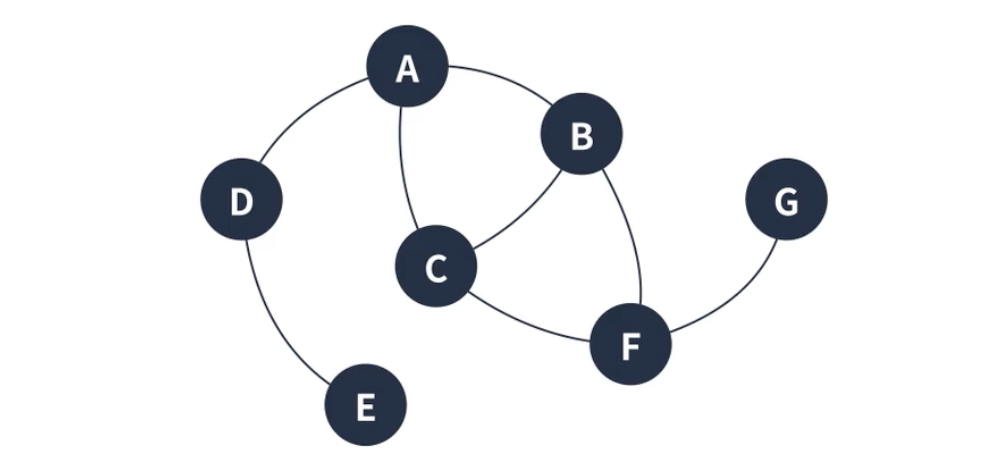
무방향 그래프

무방향 그래프 는 간선으로 이어진 정점끼리 양방향으로 이동이 가능하다. 표현하기에 (A, B)와 (B, A)는 같은 간선으로 취급된다.

e.g. 양방향 통행 도로

무방향 그래프

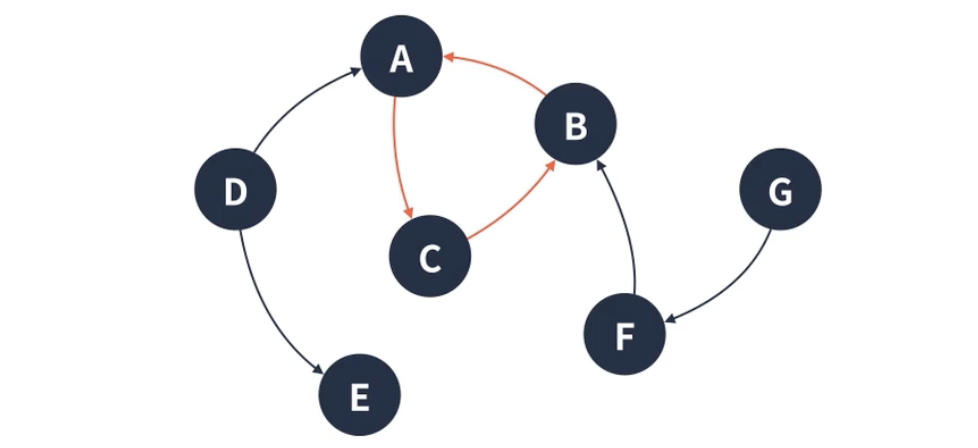
방향 그래프

방향 그래프 는 간선에 방향이 존재하는 그래프다. 양방향으로 갈 수 있더라도 <A, B>와 <B, A>는 다른 간선으로 취급된다.

e.g. 일방 통행

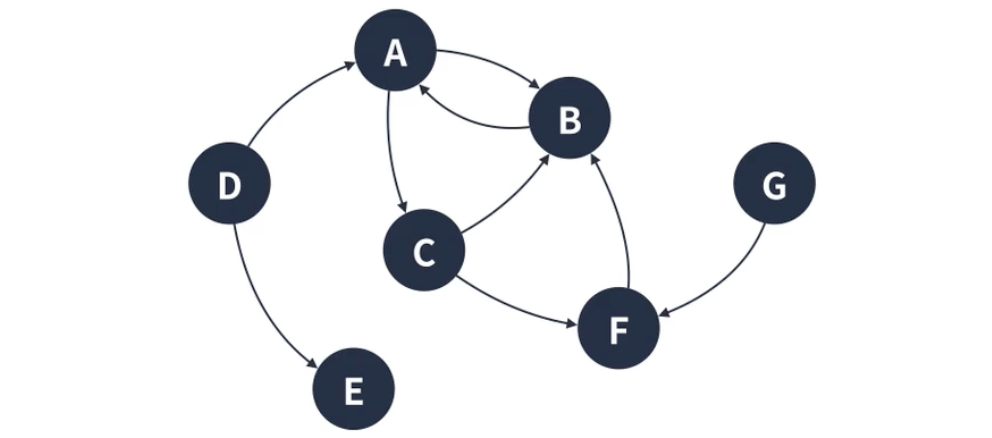
방향 그래프

연결 상태로 분류하는 그래프

간선에 방향성이 아닌 전체 그래프의 연결 상태로 분류를 하는 그래프는 3가지가 있다.

연결 그래프

연결 그래프 는 모든 정점이 서로 이동 가능한 상태인 그래프다

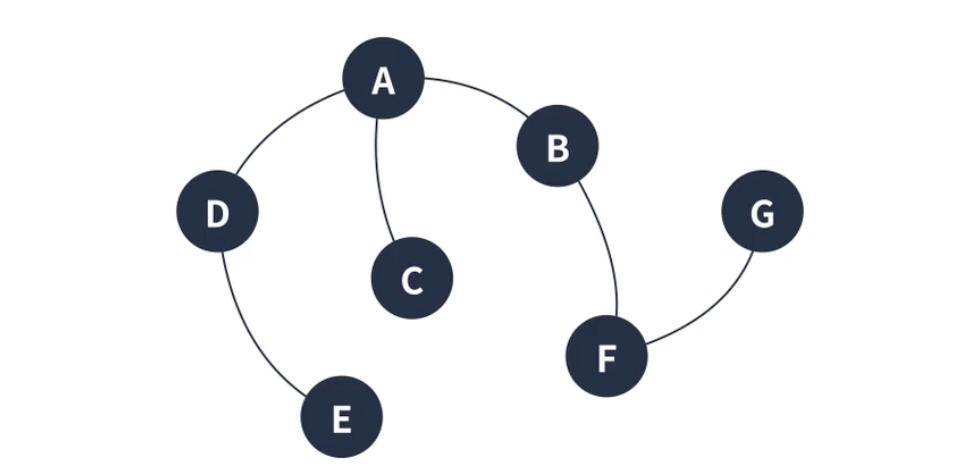
연결 그래프

특정 정점에서 다른 특정 정점까지 모든 경우의 수가 가능해야한다.

비연결 그래프

비연결 그래프 는 특정 정점쌍 사이에 간선이 존재하지 않는 그래프다.

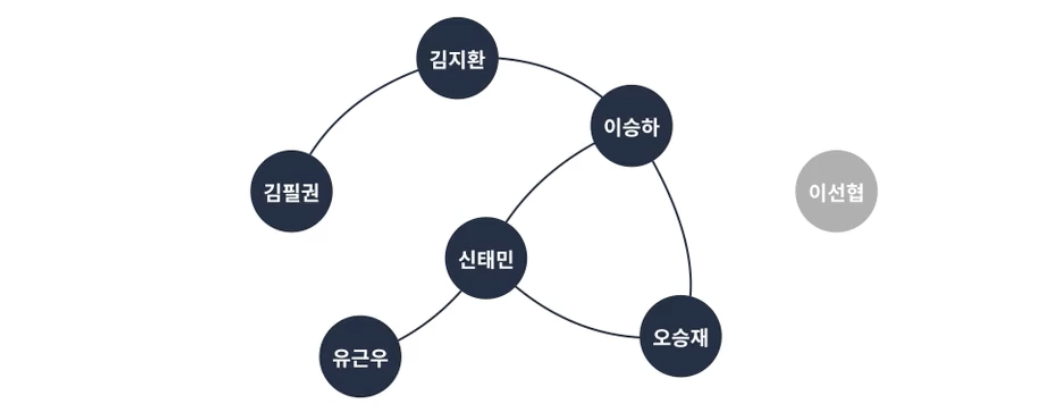
비연결 그래프

완전 그래프

완전 그래프 는 모든 정점끼리 연결된 상태인 그래프다.

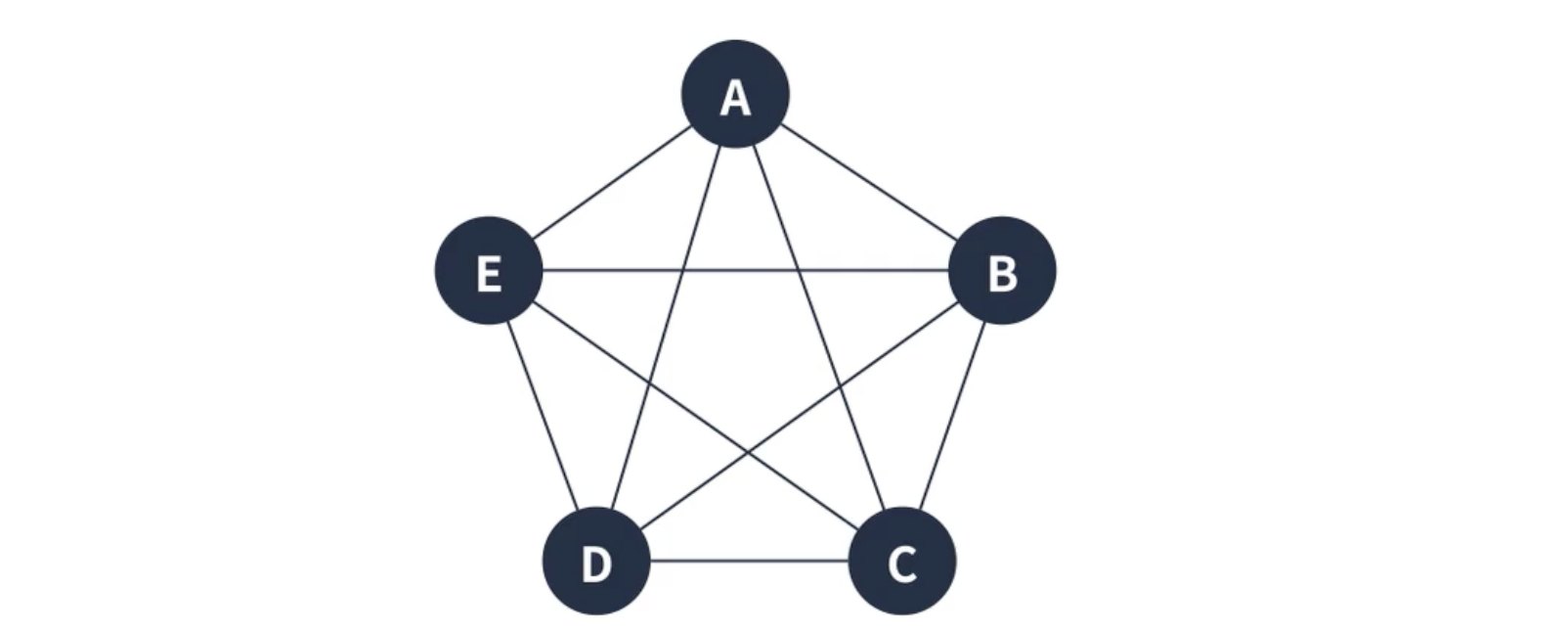
완전 그래프

한 정점의 간선 수 = 모든 정점 수-1
모두 간선 수 = 모든 정점 수-1 * 모든 정점수

JavaScript 그래프 사용법

인접 행렬, 인접 리스트 두 가지 방식으로 그래프를 표현할 수 있다.

인접 행렬 은 이차원 배열을 이용할 수 있다.
인접 리스트 는 연결 리스트로 표현이 가능하다.

인접 행렬

const graph = Array.from(
	Array(5),
  	() => Array(5).fill(false)
);

graph[0][1] = true;  // 0 -> 1
graph[0][3] = true;  // 0 -> 3
graph[1][2] = true;  // 1 -> 2
graph[2][0] = true;  // 2 -> 0
graph[2][4] = true;  // 2 -> 4
graph[3][2] = true;  // 3 -> 2
graph[4][0] = true;  // 4 -> 0

정점의 크기만큼 2차원 배열을 생성한다.
연결이 되어있지 않은 상태에서 초기화한다.
행렬의 열부분을 시작종점, 행부분을 도착종점으로 설정한다.
true 를 넣어주면, 간선이 연결되어진다.

만약 간선의 가중치를 넣고싶다면, false와 true가 아닌 null 과 임의의 값 을 넣어주면 된다. 무방향 그래프를 구현하려면 모든 값을 대칭으로 넣어주어야 한다.

인접 리스트

const graph = Array.from(
	Array(5),
  	() => []
);
graph[0].push(1);  // 0 -> 1
graph[0].push(3);  // 0 -> 3
graph[1].push(2);  // 1 -> 2
graph[2].push(0);  // 2 -> 0
graph[2].push(4);  // 2 -> 4
graph[3].push(2);  // 3 -> 2
graph[4].push(0);  // 4 -> 0

자바스크립트에서 배열은 마치 연결리스트처럼 무한정 늘어날 수 있는 장점을 지니고 있다.

정점의 수만큼 배열을 생성한다.
연결할 정점을 배열에 추가한다.

실제 소프트웨어 활용

지하철 노선도 에서 각 정점이 지하철역이 되고, 지하철역과 역 사이의 간선은 이동 시간 정보를 가지고 있다.
페이지 랭크 알고리즘 은 구글이 존재할 수 있게한 검색 알고리즘이다. 하나의 페이지가 정점이 되고, 페이지에서 파생되는 링크들이 간선이 된다. 페이지 랭크는 이런 방식으로 페이지와 링크를 수집하여 우선도를 측정하고 검색 결과를 계산한다.