[Data Structure] 트리(Tree)

트리(Tree)란?

트리(Tree) 는 방향 그래프의 일종으로 정점을 가리키는 간선이 하나밖에 없는 구조를 가지고 있다.

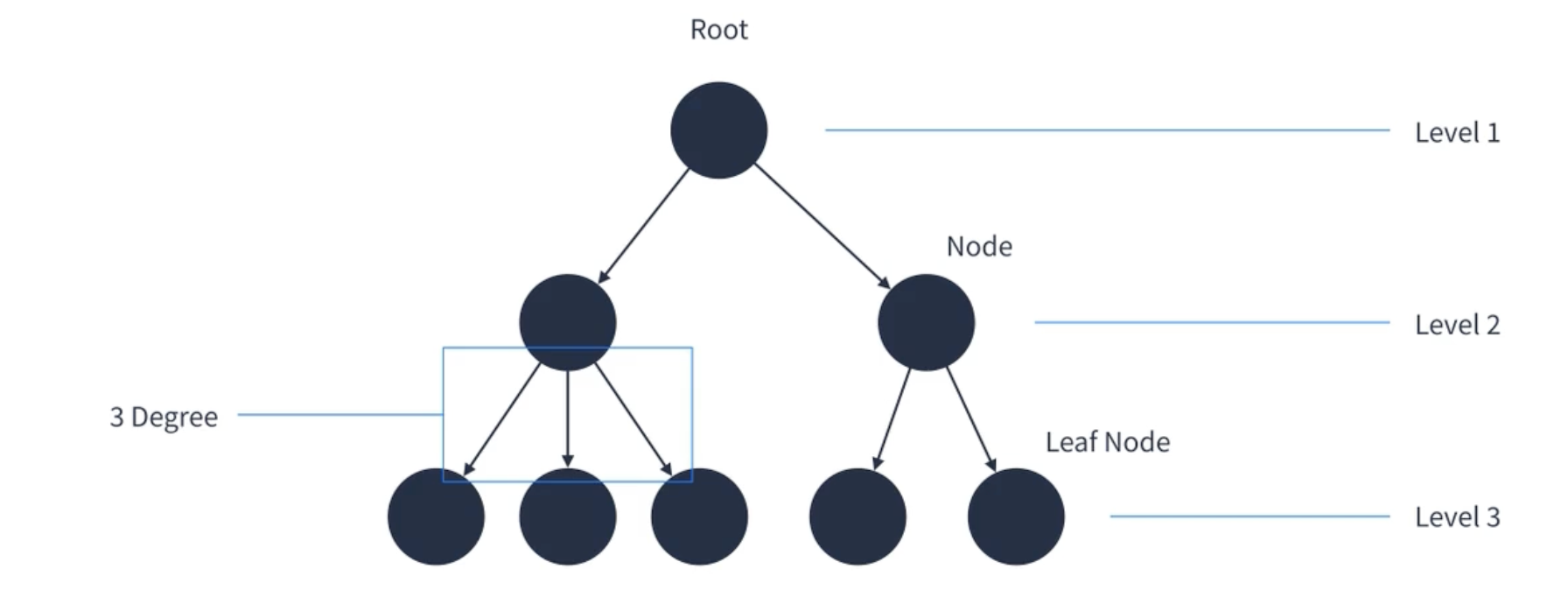
하나의 루트에서 하위로 뻗어나가는 구조다.

Tree의 정의

• Tree 는 이름 그대로 나무를 거꾸로 뒤집어 높은 모습을 가지고 있다.

• 그래프의 여러 구조 중 단방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아다고 해서 트리 구조라고 부른다.

• 데이터가 바로 아래에 있는 하나 이상의 데이터에 한 개의 경로와 하나의 방향으로만 연결된 계층적 자료구조다.

• 데이터를 순차적으로 나열시킨 선형 구조가 아니라, 하나의 데이터 아래에 여러 개의 데이터가 존재할 수 있는 비선형 구조다.

• 트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가기 때문에 사이클(cycle)이 없다. 여기서 사이클(cycle) 이란 시작 노드에서 출발해 다른 노드를 거쳐 시작 노드로 돌아올 수 있다면 사이클이 존재한다고 표현한다.

• 따라서 트리는 사이클(cycle)이 없는 하나의 연결 그래프 (Connected Graph)라고 할 수 있다.

Tree의 구조와 특징

특징

• 루트 정점을 제외한 모든 정점은 반드시 하나의 부모 정점을 가진다.
• 정점이 $N$개인 트리는 반드시 $N-1$개의 간선을 가진다.
• 루트에서 특정 정점으로 가는 경로는 유일하다.

깊이 (depth)

트리 구조에서는 루트로부터 하위 계층의 특정 노드까지의 깊이(depth)를 표현할 수 있다.

레벨 (Level)

트리 구조에서 같은 깊이를 가지고 있는 노드를 묶어서 레벨(level)로 표현할 수 있다. 깊이가 0인 루트는 level 1로 볼수 있으며, 깊이가 1인 노드는 level 2로 볼 수 있다.

같은 레벨에 나란히 있는 노드를 형제 노드(Sibling Node) 라고 한다.

높이 (Height)

트리 구조에서 리프 노드를 기준으로 루트까지의 높이(height)를 표현할 수 있다. 리프 노드와 직간접적으로 연결된 노드의 높이를 표현하며, 부모 노드는 자식 노드의 가장 높은 높이 값에 +1한 값을 높이로 가진다.

서브 트리 (Sub tree)

트리 구조의 루트에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리를 서브 트리라고 부른다.

---

용어 정리

• Root(루트) : 트리 구조의 시작점이 되는 노드 (가장 상위에 존재하는 정점)
• Node(노드) : 트리 구조를 이루는 모든 개별 데이터 (각 정점)
• Parent node(부모 노드) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
• Child node(자식 노드) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루크에서 먼 노드
• Leaf(리프) : 트리 구조의 끝 지점이고, 자식 노드가 없는 노드 (더 이상 자식이 없는 정점)
• Level(레벨) : root로부터 몇 번째의 깊이인지를 표현
• Degree(차수) : 한 정점에서 뻗어나가는 간선 수

이진 트리 (Binary tree)

이진 트리 (Binary tree) 는 각 정점이 최대 2개인 자식을 가지는 트리를 의미한다. 이 두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있다.

이진 트리는 자료의 삽입, 삭제 방법에 따라 여러 종류로 나뉜다.

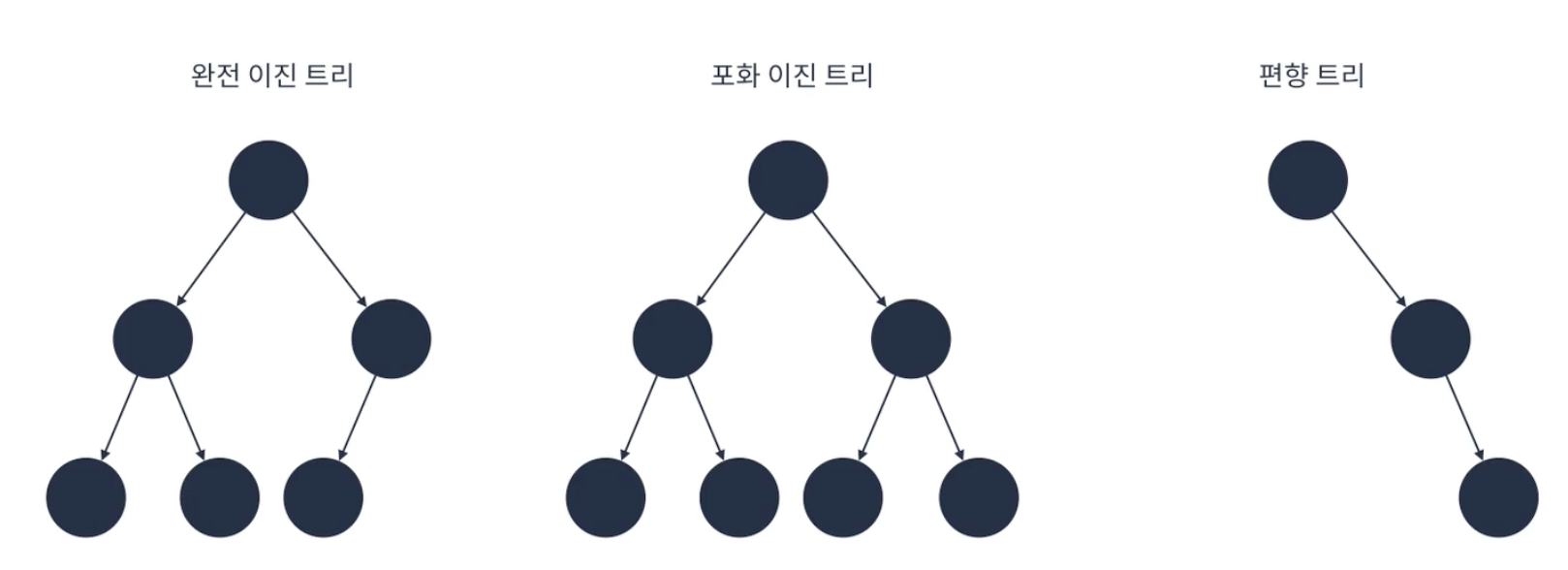
이진 트리의 특징

• 정점이 $N$개인 이진 트리는 최악의 경우 높이가 $N$이 될 수 있다.
• 정점이 $N$개인 포화 또는 완전 이진 트리의 높이는 $log N$이다.
• 높이가 $h$인 포화 이진 트리는 $2^h$-$1$개의 정점을 가진다.
• 일반적으로 이진 트리를 사용하는 경우는 많지 않다.
  • 이진 탐색 트리, 힙, AVL 트리, 레드 블랙 트리 와 같은 자료구조에 응용된다.

완전 이진 트리

• 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야한다.
• 높이가 $h$이고, 노드 수가 $n$개일 때, 노드 번호 1번부터 $n$번까지 빈 자리가 없는 이진 트리
• 노드 개수 : $2^h$-$1$ <=  $n$  <=  $2^h$-$1$

포화 이진 트리

• 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리다.
• 트리 구성하는 노드의 차수가 0 또는 2이면서 높이가 $h$일 때, 최대의 노드 개수인 $(2^h$-$1)$개의 노드를 가진 이진 트리
• 루트를 1번으로 하여 $2^h$-$1$까지 정해진 위치에 대한 노드 번호를 가진다. (레벨이 같을 때는 왼쪽에서 오른쪽으로 번호를 붙임)
• 레벨 i에서 노드의 수 : $2^{i-1}$

사향(편향) 이진 트리

• 높이 $h$에 대한 최소 개수의 노드를 가지면서 한쪽 방향 자식 노드만을 가진 이진 트리다.
• 왼쪽 편향 이진 트리 : 모든 노드가 왼쪽 자식 노드만을 가진 편향 이진 트리
• 오른쪽 편향 이진 트리 : 모든 노드가 오른쪽 자식 노드만을 가진 편향 이진 트리

JavaScript 트리 사용법

트리의 구현 방법도 그래프와 마찬가지로 인접 행렬, 인접 리스트 두 가지 방식으로 트리를 표현할 수 있다.

이진 트리의 경우에는 자식이 2개 이하로 제한되는 특징 때문에 조금 더 최적화된 방식으로 구현이 가능하다. 1차원 배열 혹은 링크가 2개가 존재하는 연결 리스트로 구현이 가능하다.

• 인접 행렬 은 이차원 배열을 이용할 수 있다.
• 인접 리스트 는 연결 리스트로 표현이 가능하다.

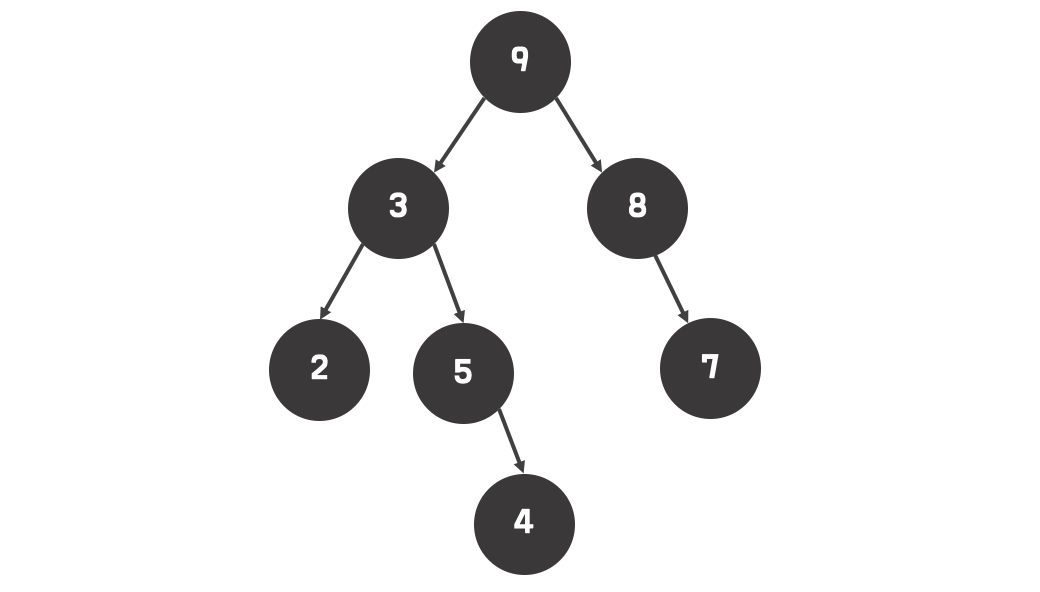
위에 보이는 사진처럼 이진트리를 각각의 코드로 작성하면 다음과 같다.

인접 행렬

// 0번 인덱스는 편의를 위해 비워둔다.
// Left 정점 = Index * 2
// Right 정점 = Index * 2 + 1
// Parent 정점 = floor(Index / 2).  // Index를 2로 나누고 소수점을 버림
const tree = [
  undefined,
  // 1
  9,
  // 1*2, 1*2+1
  3, 8,
  // 2*2, 2*2+1, 3*2, 3*2+1
  2, 5, undefined, 7,
  // 4*2, 4*2+1, 5*2, 5*2+1
  undefined, undefined, undefined, 4
];

인접 리스트

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class Queue {
  constructor() {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  enqueue(value) {
    const newNode = new Node(value);
    if (!this.head) {
      this.head = this.tail = newNode;
    } else {
      this.tail.next = newNode;
      this.tail = newNode;
    }
    this.size += 1;
  }

  dequeue() {
    const value = this.head.value;
    this.head = this.head.next;
    this.size -= 1;
    return value;
  }

  peek() {
    return this.head.value;
  }
}

class Tree {
  constructor(node) {
    this.root = node;
  }

  display() {
    const queue = new Queue();
    queue.enqueue(this.root);
    while (queue.size) {
      const currentNode = queue.dequeue();
      console.log(currentNode.value)
      if (currentNode.left) queue.enqueue(currentNode.left);
      if (currentNode.right) queue.enqueue(currentNode.right);
    }
  }
}

const tree = new Tree(new Node(9));
tree.root.left = new Node(3);
tree.root.right = new Node(8);
tree.root.left.left = new Node(2);
tree.root.left.right = new Node(5);
tree.root.right.right = new Node(7);
tree.root.left.right.right = new Node(4);
console.log(tree.display());

트리 활용

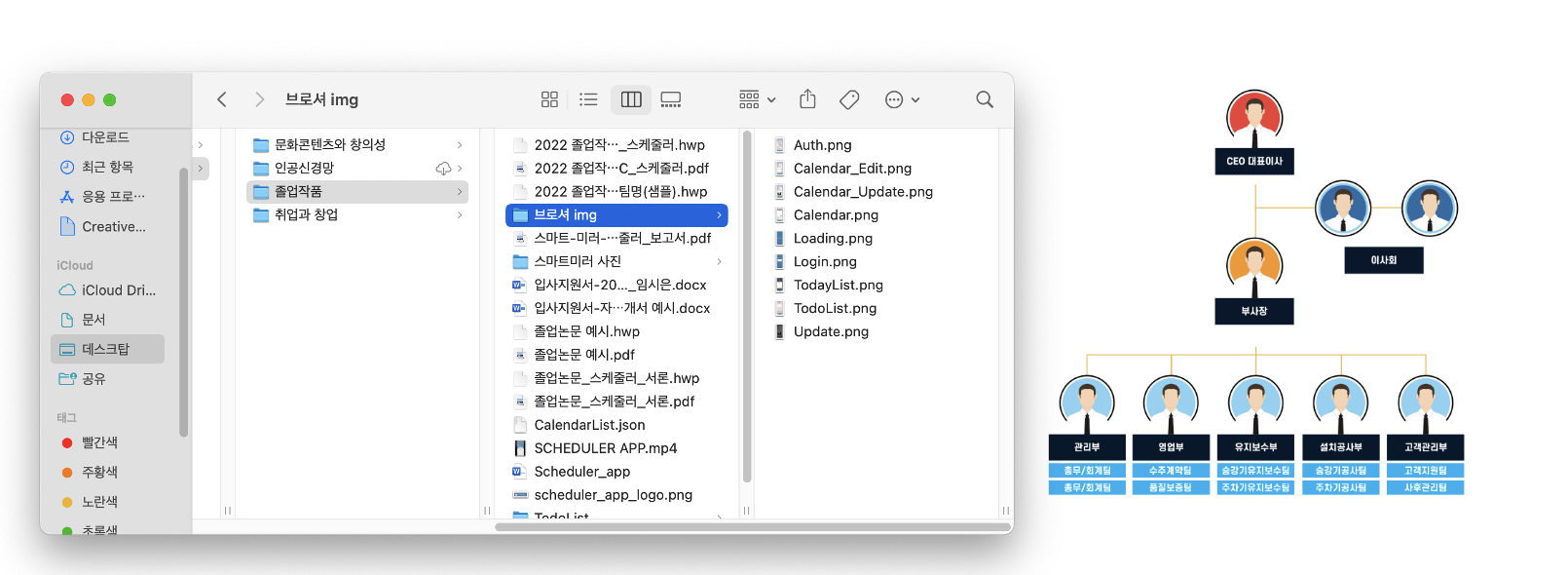
대표적으로 트리를 활용한 것은 조직도와 디렉터리 구조가 있다.

Reference

프로그래머스 코딩 테스트 광탈 방지 A to Z : JavaScript
CODESTATES (SEB_FE_43)