개념정리하는 정도?
선형 구조
Stack (스택)
스택은 후입선출(Last In First Out) 또는 선입후출(First In Last Out) 이라고 부른다.
즉, 가장 나중에 넣은 것을 먼저 꺼낼 수 있는 자료구조로
데이터를 넣을 때는 Push() 를 데이터를 꺼낼때는 PoP()을 사용한다.
프링글스 감자칩이 딱 스택 자료구조와 닮아 있다. 꺼내먹을땐 가장 상단에서 부터 꺼내 먹어야하니까..!
특징
- 한번에 여러개의 데이터를 못꺼낸다.
pop()을 사용하여 하나씩 꺼낼 수 밖에 없다. - 하나의 입출력 방향을 가지고 있다.
데이터를 넣고 꺼내는 방향은 스택의 가장 최상단 에서만(프링글스 뚜껑을 통해서만)
브라우저에서 앞으로가기 뒤로가기를 구현할때 스택 자료구조를 이용할 수 있다.
Queue (큐)
큐는 선입선출(First In First Out) 또는 후입후출(Last In Last Out) 이라고 부른다.
즉, 가장 먼저 넣은 것은 가장 먼저 꺼낼 수 있는 자료구조로
데이터를 넣는 것을 enqueue 꺼내는 것을 dequeue 라고 부른다.
고속도로 톨게이트가 딱 큐 자료구조와 닮아 있다. 먼저 들어온 차가 먼저 요금을 계산하고 나갈 수 있으니까..!
특징
- 한번에 여러개의 데이터를 못꺼낸다.
스택과 마찬가지로 한번에 하나의 데이터만을 꺼낼 수 있다. - 두개의 입출력 방향을 가지고 있다.
스택과 다르게 데이터를 넣는 방향과 데이터를 꺼내는 방향이 서로 다르다.
데이터를 넣을 때는 큐의 맨끝으로만 넣을 수 있고 데이터를 꺼낼 때에는 큐의 맨 앞으로만 꺼낼 수 있다.
비선형 구조
하나의 데이터에 여러개의 데이터가 존재할 수 있는 구조
Tree (트리)
트리 자료구조는 나무를 뒤집에 놓은 형태로 단방향 그래프의 한구조로 나무의 가지처럼 사방으로 뻗은 형태이다.
용어
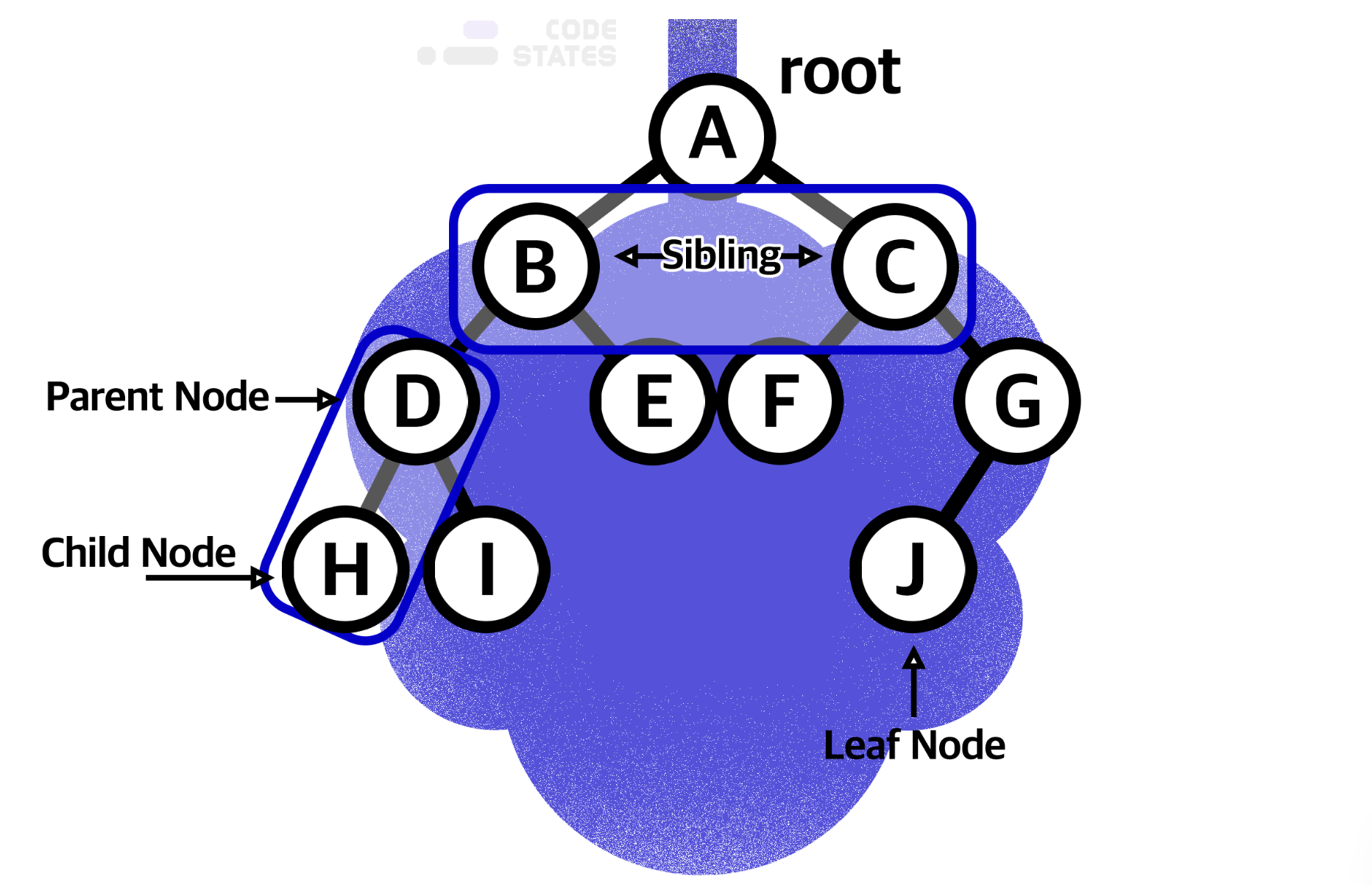
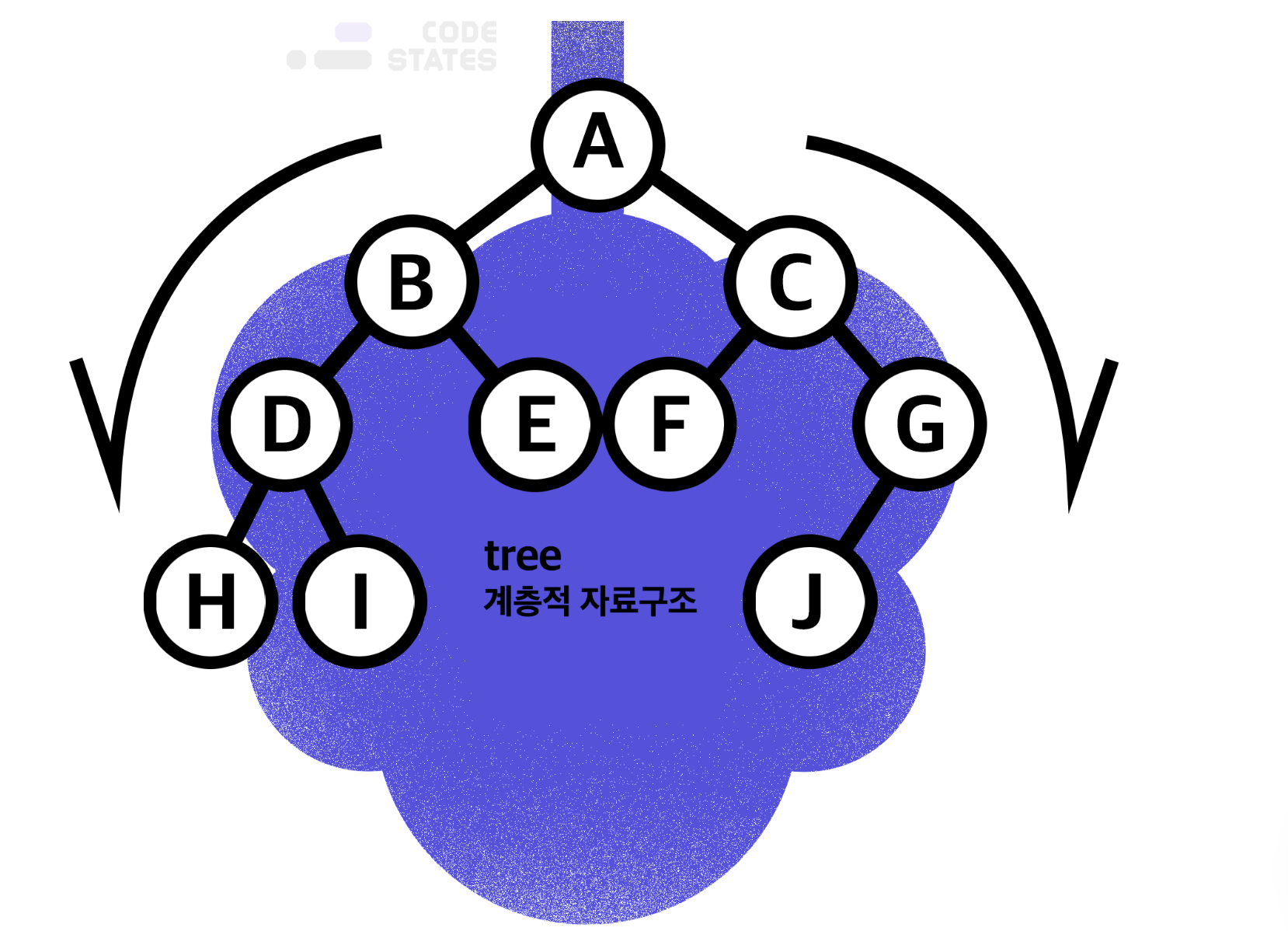
각 데이터들을(A,B,C,,,) 노드라고 부른다.
- root : 최상단에 있는 노드를 root 노드라고 부른다.
- parent node : 두개의 노드가 상하 계층으로 연결된 경우 상위에 있는 노드
- child node : 두개의 노드가 상하 계층으로 연결된 경우 하위에 있는 노드
- Leaf node : 더이상 자식노드가 없는 노드
- sibling : 같은 레벨에 있는 노드 (형제노드)
이진트리 (Binary Tree)
이진트리는 자식노드가 최대 두 개인 노드로 구성된 트리이다. 자식노드는 왼쪽 자식노드와 오른쪽 자식노드로 나눌 수 있다. 위의 사진도 이진 트리 구조로 되어있다.
이진 탐색 트리 (Binary Serch Tree)
이진트리와 비슷하지만 다르다.
이진 탐색 트리는 데이터가 정렬되어 있다. 즉 root 노드를 기준으로 왼쪽 자식노드들은 root 노드보다 항상 작은 값을 가지고 오른쪽 자식노드들은 root 노드보다 항상 큰 값을 가진다.
그렇기 때문에 정렬된 데이터 속에서 원하는 숫자를 찾는데 걸리는 시간은 O(logn) 만큼 걸린다.
O(logn) 은 O(n)의 절반을 나타낸다.!
이진 트리에서는 데이터가 정렬되어 있지 않기 때문에 원하는 숫자를 찾을려면 처음부터 끝까지 찾아보는 수 밖에 없다. 이때 시간이 O(n) 만큼 시간이 소비된다.
트리 순회 방법
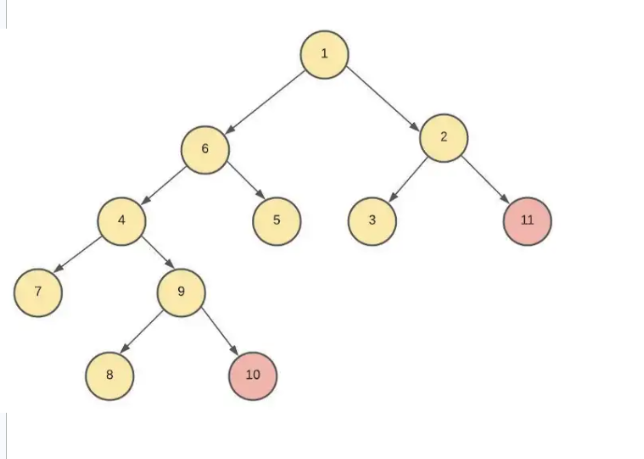
해당 이진 트리를 순회해보자
1. 전위 순회
루트노드 -> 왼쪽 노드 -> 오른쪽 노드 으로 탐색하는 방법
전위 1 6 4 7 9 8 10 5 2 3 11
2. 중위 순회
왼쪽 노드 -> 루트노드 -> 오른쪽 노드 로 탐색하는 방법
중위 7 4 8 9 10 6 5 1 3 2 11
3. 후위 순회
왼쪽 노드 -> 오른쪽 노드 -> 루트 노드로 탐색하는 방법
후위 7 8 10 9 4 5 6 3 11 2 1
Graph (그래프)
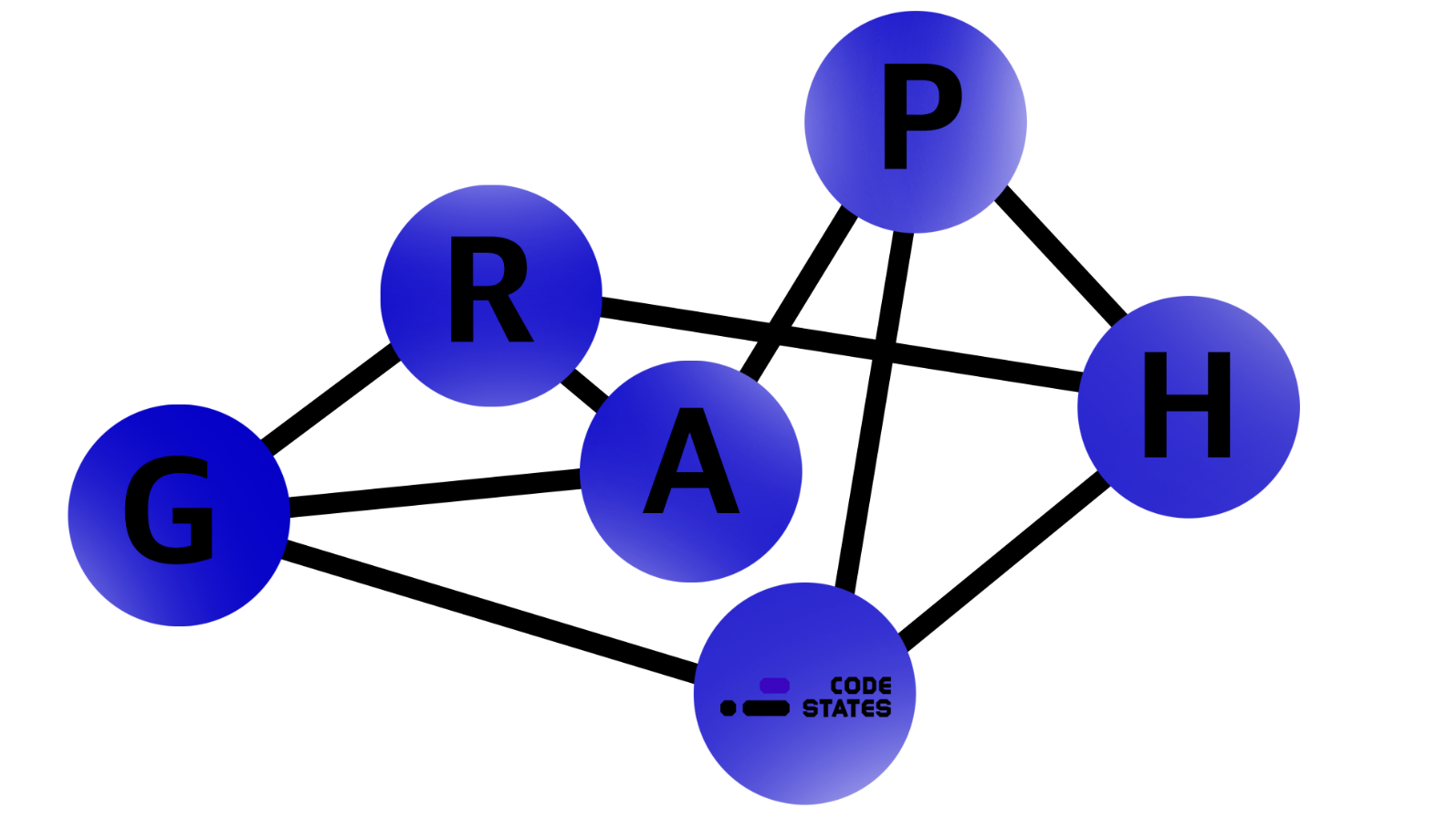
그래프는 여러 개의 정점이 간선으로 복잡하게 이어져 있는 구조
정점이란 사진상의 알파벳인 데이터를 나타내는 단어
간선이란 데이터끼리 연결되어 있는 선
직접적인 관계 : 간선으로 연결되어 있으면
간접적인 관계 : 직접적으로 연결되어 있진 않고 다른 정점에 의해 간접적으로 엮여있는 경우
BFS
너비 우선 탐색으로 같은 레벨의 데이터를 탐색하는 방법으로 두 정점 사이의 최단 경로를 찾을 때 사용한다.
DFS
깊이 우선 탐색으로 하나의 정점에서 부터 시작하는데 그 정점의 자식까지 다 확인하고 그 다음 정점을 확인하는 방식 모든 노드를 완전히 탐색할 수 있음
사진출처 : 코드스테이츠
