01 QM-Method
K-Map 의 한계는 확장성에 있다.
- 입력 변수가 많은 경우는? -> QM-Method !
QM-Method 활용 시 알고리즘 단순화를 할 수 있다.
hamming distance 가 1 인 것을 알고 싶을 때, 1의 개수가 1 차이나는 것을 알아본다.
✋ 그런데, hamming distance 가 1이 안되는 경우가 있다.
- 0010
- 0101
이 경우, 1의 개수가 1 차이나서 hamming distance 가 1인 가능성은 있지만, 실제 계산해보니 3 차이났다. 하지만 이런 overhead 를 감수하면서 탐색 범위를 줄이기 위해 사용하는 방법이 바로 QM-Method 이다.
Step 1: Find PI's
m(0,4,8,10,11,12) + d(13,15)
-> d는 don't care conditions: 차별하지말고 그냥 다 적는다.
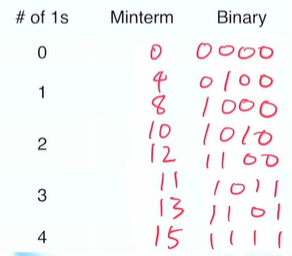
먼저, Binary format 으로 변환해준다.
0 -> 0000
4 -> 0100
8 -> 1000
10 -> 1010
11 -> 1011
12 -> 1100
13 -> 1101
15 -> 1111
그 다음, 1의 개수에 따라 정렬해줘야한다.
0 -> 0000
4 -> 0100
8 -> 1000
10 -> 1010
12 -> 1100
11 -> 1011
13 -> 1101
15 -> 1111
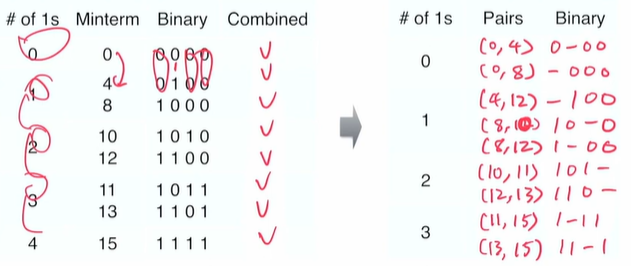
- Find all implicants with size 1
Minterm 0 의 경우 # of 1s 가 0인데, 어떤 애들과 대조를 해보면 될까? -> # of 1s 가 1인 애들 (4,8) !
이렇게 하면 대조를 해야하는 computational 양을 현저히 많이 줄일 수 있다.
⭐ 여기서 # of 1s 가 같은 애들끼리는 hamming distance 가 1이 될 수 없다.
-> 같은 구역에 있는 애들끼리는 비교할 필요는 없다.
- Find all implicants with size 2
따라서, Minterm 0과 4,8 비교 - Minterm 4와 10,12 비교 - Minterm 8과 10,12 비교 ... 이런 식으로 진행한다.
- Find all implicants with size 4
⭐ quadra 를 할 때는 정확하게 패턴이 일치해야한다!
예를 들어, Pair (0,4) 와 (8,12) 를 비교할 때, '-' 을 고유의 symbol 이라고 생각한다.
0 - 0 0
1 - 0 0
0과 1이 병합 가능하고, 나머지 뒤에 패턴이 똑같으니 Combined 된다고 볼 수 있다.
Step 2: Find EPI's
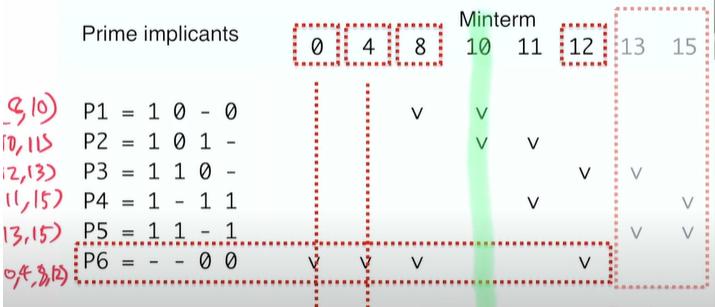
먼저, Scan 을 해준다. don't care condition 은 해줄 필요 없다.
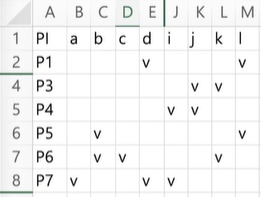
- Find all columns with only a single 'v'
- Minterm 0
Minterm 0을 누가 책임질 수 있는지 봤더니, P6에만 v 가 되어있다. 이 말은, P6가 반드시 들어가야한다는 말이다.
P6는 (0,4,8,12) 이니까 4,8,12 는 어떻게 커버해야하는지 걱정할 필요가 없어진다. (4,8,12 에도 v 체크 !)
이제 Minterm 10으로 넘어가서 스캔해도 무방하다.
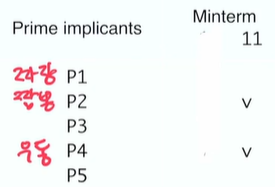
- Minterm 10
이 경우, P1, P2 가 NEPI 이다.
-> 결론적으로 P6가 EPI 라는 것이 확인됐다.
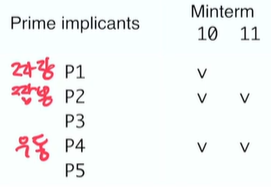
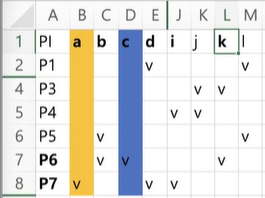
- 다른 예제이다.
P2, P3, P5 가 EPI / P1, P4 는 NEPI 가 된다.
🐣 이때, P1, P4가 신경써줘야하는 애는 누구일까? -> 바로 Minterm 9 이다.
Minterm 9를 커버해주는 애가 없으므로 Minterm 9가 있는 P1 과 P4를 확인한다. 여기서 P4가 coverage 가 더 크므로 P4를 채택한다.
Step 3: Determine a Minimum Cover
다시 기존 예제로 돌아가면 ..
- 기존 예제
여기서 Minterm 10과 11은 NEPI 인데, NEPI 중에서도 minimum cover 를 찾는다.
-> 들어가는 PI 의 개수를 줄이는 것이 cost 를 줄이는 것과 동일하기 때문이다.
😊 But, reducing the table is not mandatory, but for your convenience.
이 테이블에서 P1, P2, P4의 cost 가 같다. -> 3 input - AND gate (cost 4)
어떻게 구별하냐면 '-' 의 개수로 알 수 있다. '-' 의 개수가 없어질 수록 비싸진다.
'-' 이 아예 없는 경우 -> 4 input - AND gate (cost 5)
3-1. Row Dominance
dominant 하는 친구만 살리고, dominant 당하는 친구는 빼면 optimal solution 을 구하는데에 아무 문제가 없다.
⭐ 참고로 가로줄의 v 체크 개수가 가장 많은 PI가 지배하는 친구다.
dominant 당하는 P1을 빼게 되면, P2가 Secondary EPI 가 된다.
추가로 전수조사를 한다.
P2와 P4를 비교해봤을 때 P2가 P4를 지배한다.
따라서, 이런 테이블이 완성된다.
3-2. Column Dominance
반대로 dominant 하는 친구를 빼고, dominant 당하는 친구를 살린다.
⭐ 참고로 세로줄의 v 체크 개수가 가장 많은 PI가 지배하는 친구다.
- 설명을 위해 다른 예제 사용
Minterm 10은 상대적으로 둥글둥글한 애이다. 까다로운 Minterm 11에게 메뉴 주문을 시키는게 더 바람직하다.
따라서, Coverage 가 좁은 애가 남아 있는다.
Row dominance 와 Column dominance 중에 뭐를 먼저 할지는 상관없다.
다시 원래 예제로 돌아와서 ..
- 최종 솔루션: f = P2 + P6 = x1x2'x3 + x3'x4'
Row dominance 와 Column dominance 를 확인해봤을 때 테이블에 변화가 생긴다면 Secondary EPI 가 생겼는지 다시 한번 확인하고 마지막 단계까지 소거되지 않는 NEPI 가 나올 때까지 구하면 된다.
여기서 만약 NEPI 가 3개 나온다고 가정할 때, 2^3 = 8가지 케이스를 테스트 해봐야한다. 각각의 NEPI 를 넣을지 말지 원래는 다 해봐야하는데 여기서 확실하게 하는 방법이 있을지는 Patrick's Method 에서 진행한다.
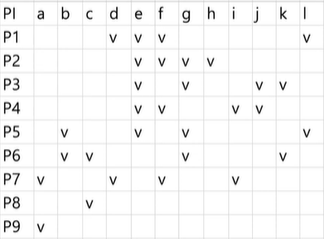
추가 예제 풀이
⭐ Step 2: EPI 를 찾는다.
여기서는 h 를 담당하는 P2가 EPI 가 된다. 이로써 P2의 e,f,g,h 가 같이 커버된다.
g 와 h 관계를 봤을 때, h 는 굉장히 까다로운 친구다. 그렇다면 g 를 빼준다.
f 와 h 관계를 봤을 때, f 를 빼준다.
e 와 h 관계를 봤을 때, e 를 빼준다.
-> h 만 채택해도 e,f,g 는 자동으로 따라오니 어떻게 보면 우리도 모르게 column dominance 의 역할을 이미 수행하고 있다고 볼 수 있다.
이 스텝에서 일단 f = P2 가 들어갔다.
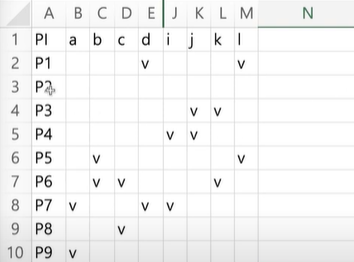
- e,f,g,h 숨김
해당하는 e,f,g,h 를 뺐더니 P2의 v 체크가 없어졌다. 그렇다면 소거가 가능해진다.
- P2 숨김
이렇게 되니 테이블이 꽤 줄었다. 여기서 더이상 EPI가 안보이니 Step 3로 넘어간다.
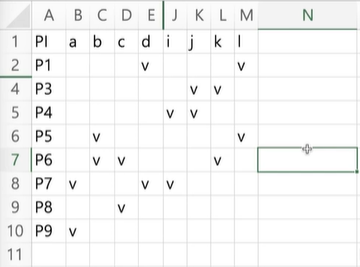
⭐ Step 3: Column dominance 를 체크한다.
- P2 숨김
이 테이블에서 Column dominance 가 보이지 않는다. Column dominance 를 시도했는데 테이블에 변화가 없으므로 Secondary EPI 를 찾는 스텝으로 돌아가는 것이 의미가 없다. 이때, Row dominance 도 시도해본다.
P6-P8, P7-P9 사이에 Row dominance 가 존재한다.
- P8, P9 숨김
까다로운 P8, P9을 빼준다.
테이블에 변화가 생겼으니 이제 Step 2: Secondary EPI 를 찾는 단계로 돌아간다.
- f = P2 + P6 + P7
여기서 P6와 P7이 Secondary EPI가 되었다.
이제 Step 3로 가서 Column / Row dominance 확인해본다.
- P6, P7 숨김 + 커버되는 Minterm 숨김
확인 결과, 테이블의 변화가 없었다. 이 말은 즉슨 더이상 Secondary EPI 가 나오지 않을 것이다.
다만 테이블이 NULL 이 아니라 까다로운 NEPI 친구들이 남아있기 때문에 우리가 어떻게든 풀어내야한다.
- 최종 솔루션: f = P2 + P6 + P7 + (P3 or P4) + (P1 or P5)
j를 커버하려면 P3나 P4를 넣어야하고, l을 커버하려면 P1이나 P5를 넣어야한다.
따라서, 4가지의 경우의 수를 확인해봐야한다.
다만, 경우의 수가 많아진다면 Patrick's Method 를 활용한다.