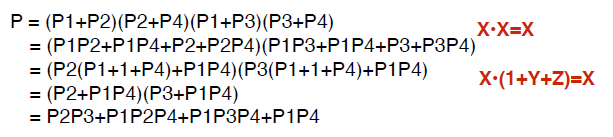[논리회로설계] Petrick's Method

02 Petrick's Method

Petrick's method allows a systematic way to find the optimal cover among NEPI's.

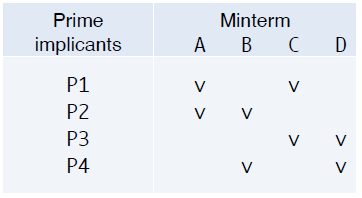
먼저, 줄이고 줄여서 Reduced chart 까지 왔다고 치자.

P1~P4는 NEPI 인데, 여기서 optimal cover 은 무엇일까?

총 경우의 수는 2^4 = 16 인데, 유효한 커버를 만들기 위해서는 P1~P4를 모두 만족해야한다.

Minterm A, B, C, D 를 모두 챙겨야하는데, A는 P1, P2밖에 못먹고 B는 P2, P4밖에 못먹고.. 그러니까 결국 최종 솔루션은 아래와 같이 POS 형태가 된다.

P = (P1+P2)(P2+P4)(P1+P3)(P3+P4)

위 식을 전개하면 다음과 같이 된다.

POS 형태가 전개 후에 SOP 형태가 된다. 이렇게 되면 P 가 1이 될 수 있는 경우만 선택하면 된다.

이때, P1, P2, P3, P4의 Cost 가 모두 같다고 가정하면, literal 의 갯수가 가장 적은 1번 or 2번을 선택하는게 Cost 적으로 유리하다.

결론적으로, optimal cover 경우의 수는 2개가 된다.

🐣 참고로, 중간중간 최적화 해주는 이유는 사용 가능한 메모리의 한계를 넘어가지 않기 위해서다.