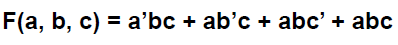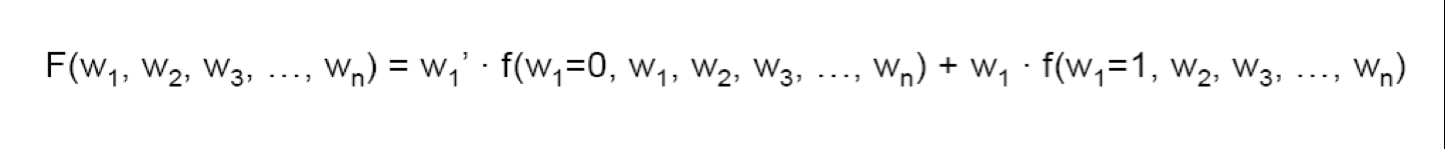05 Shannon Expansion Theorem
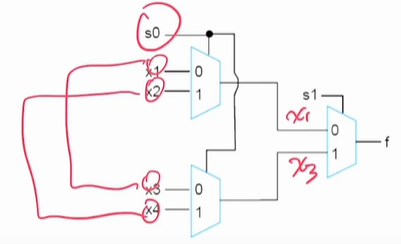
4:1 MUX Using 2:1 MUX
⭐ 만약 4:1 MUX 가 필요한데, 2:1 MUX 만 가지고 있다면? -> 2:1 MUX 로도 만들 수 있다!
- 장점: 비싼 4:1 MUX 대신 2:1 MUX 로 만들 수 있다.
- 단점: 경로가 길어진다. -> 처리 시간 증가 !
여기서 s0을 이용해서 (x1, x3) 와 (x2, x4) 를 그룹화해준다.
이후, s1을 통해 x1을 선택할지, x3를 선택할지 골라준다.
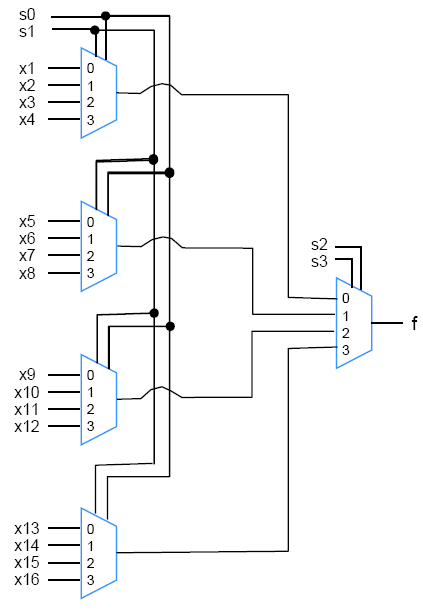
16:1 MUX Using 4:1 MUX
s0=0, s1=0 일 때 / s0=0, s1=1 일 때 ... 4:1 MUX 하나 당 4개의 경우의 수가 나오는데, 이게 4개 있으니 16개의 경우의 수가 나온다.
따라서, input 이 16개가 되고, select signal 이 4개인, 16:1 MUX 형태로 작동된다.
⭐ 4:1 MUX 던져주면 모든 2-input combination logic 을 쉽게 만들어낼 수 있다.
-> 4:1 MUX의 파워가 강력하다는 것을 알 수 있다.
XOR Gate Implementation Using MUX
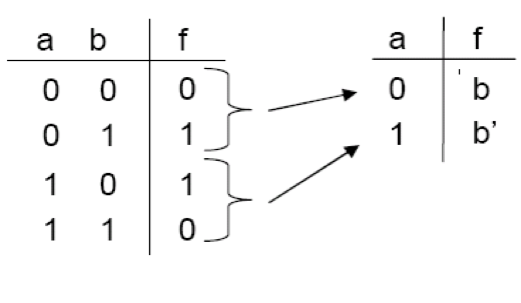
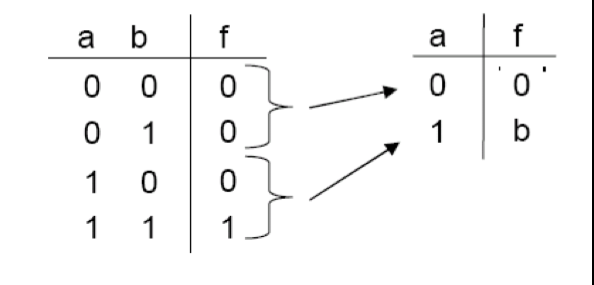
a가 0일 때 b와 f가 같고, a가 1일 때 b와 f가 같다.
XOR gate 의 truth table 을 보면 MUX 작동원리와 유사함을 볼 수 있다.
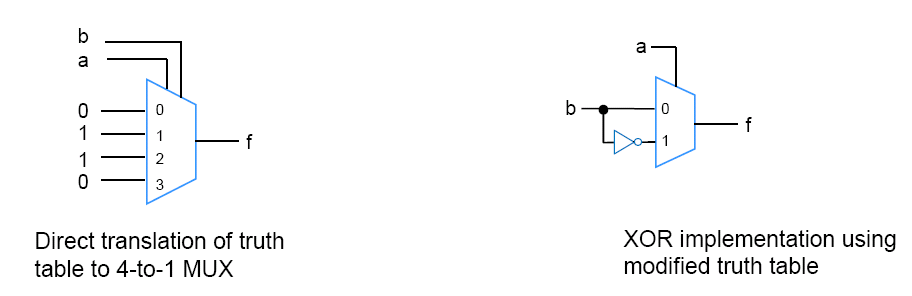
이렇게 a를 정해두고 시작한다면, 훨씬 간단한 회로를 만들 수 있다.
AND Gate Implementation Using MUX
Direct translation 의 경우 추가의 gate 투입 없이 2-input combination logic 을 바로 디자인 할 수 있다.
3-input Majority Circuit Using MUX
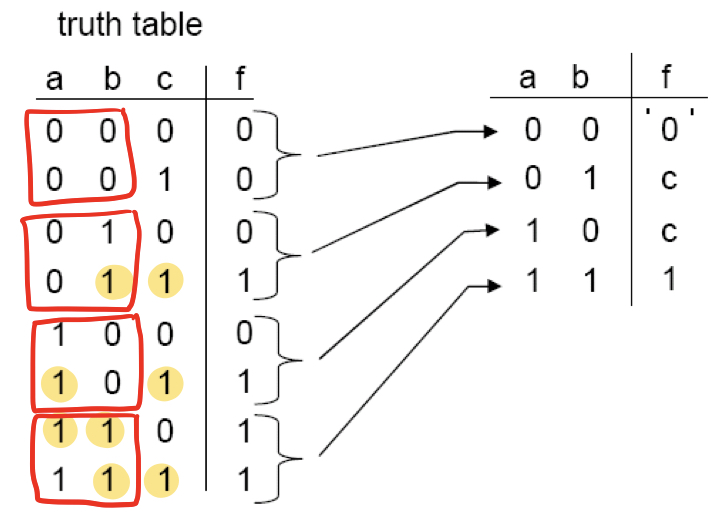
a, b, c 중에 1의 갯수가 2개 이상이면, 1을 출력한다.
만약 4:1 MUX 가 있다고 하면, 입력 3개(8줄)을 4등분해서 보겠다는 뜻이다.
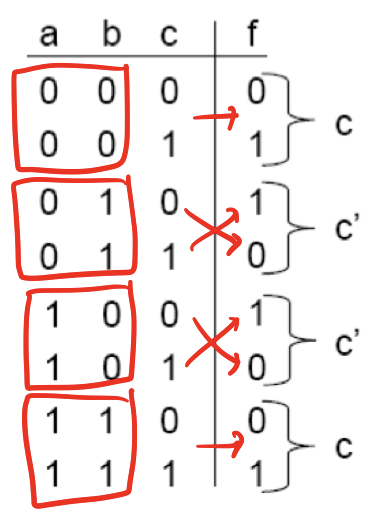
3-input XOR Circuit Using MUX
Shannon Expansion Theorem
복잡한 함수를 어떤 입력 variable 을 기준으로 이게 0 또는 1일 때, 각각에 대해서 회로를 재해석 한 것이다.
minterm 이 4개인데, a=0 일 때는 a'bc 만 살아남고, a=1 일 때는 ab'c+abc'+abc 만 살아남는다.
입력 variable 중에 하나를 고르고 expand 한다.
위의 경우, w1 을 기준으로 expand 했다.
기준이 a, b, c 냐에 따라 cost 가 각각 다를 수 있으므로, 모두 해보고 가장 낮은 cost 를 선택한다.