06 Adder
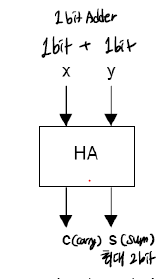
Half Adder
1-bit 2진수 두개를 더한 합 Sum(s) 과 Carry(c) 를 구하는 회로이며, 거의 1-bit 끼리의 덧셈만을 위한다.
✋ 여기서 잠깐, half adder 인 이유는 half adder 2개로 full adder 를 만들 수 있기 때문이다.
위 그림과 같이 1-bit + 1-bit 인 경우, 최대 2-bits까지 나올 수 있다.
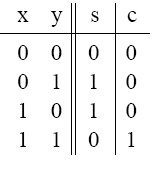
논리식은 다음과 같다.
- s = x⊕y
- c = xy
Multi-Bit Addition
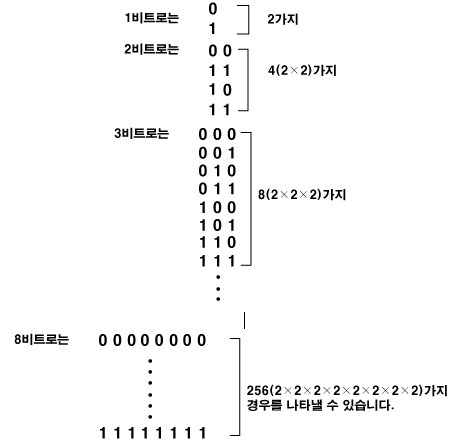
n-bits 덧셈으로 확장했을 때, truth table 사이즈가 너무 커지는 것을 알 수 있다.
-> 최적화가 잘 되지 않는다.
Two-Level Adders
input과 output 사이에 두개 이하의 논리 게이트를 사용하는 논리 설계이다.
공간복잡도: O(n^2), 시간복잡도: O(1) 을 가진다.
- 장점: 2 stages 만 통과하면 되므로 폭이 넓고 depth 는 constant 하다. (이론적으로) 성능이 향상 될 수 있다.
- 단점: gate count 가 엄청 많아져서 성능조차도 확실히 보장되지 않는다.
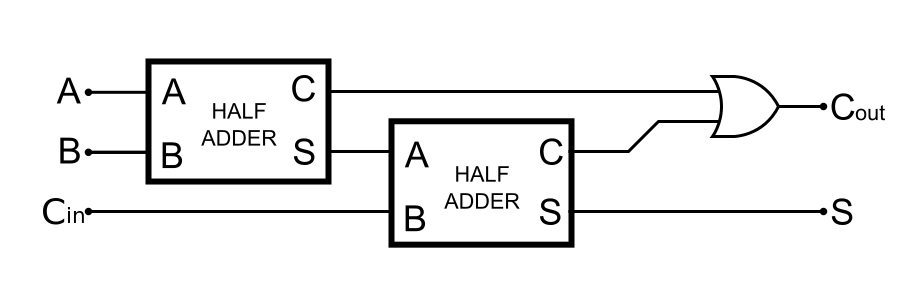
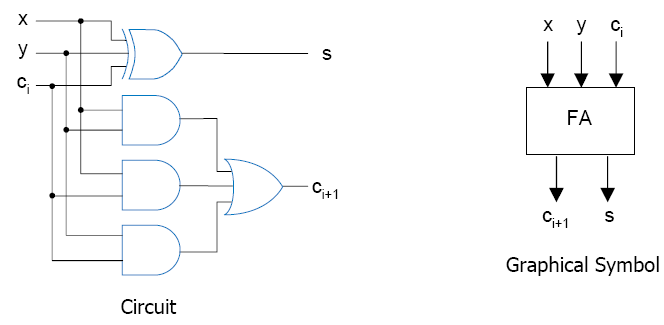
Full Adder
half adder 는 2진수 한자리 덧셈을 하므로 carry 를 고려하지 않는다. 따라서 2비트 이상의 2진수 덧셈은 할 수 없는데, 이 carry 를 고려해서 만든 덧셈 회로가 full adder 이다.
공간복잡도: O(n), 시간복잡도: O(n) 이다.
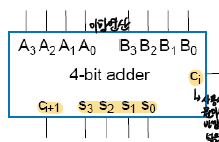
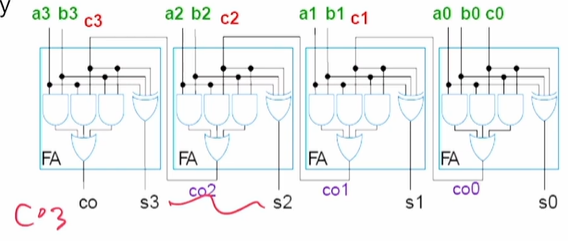
full adder 는 아랫 자릿수에서 발생한 carry 까지 포함하여 3-bits 를 더한다. 3-bits 중 한 bit 를 cin 으로 활용하면, full adder 4개를 가지고 4-bits adder 를 만들 수 있다.
논리식은 다음과 같다.
- s = x⊕y⊕cin
- c = xy+xcin+ycin
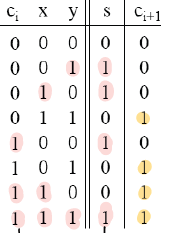
Addition with Carry
input 에서 1이 홀수일 때, s 가 XOR 3-input 패턴과 일치하는 것을 볼 수 있다.
1-bit adder를 4-bits로 구현할 수 있다.(??)
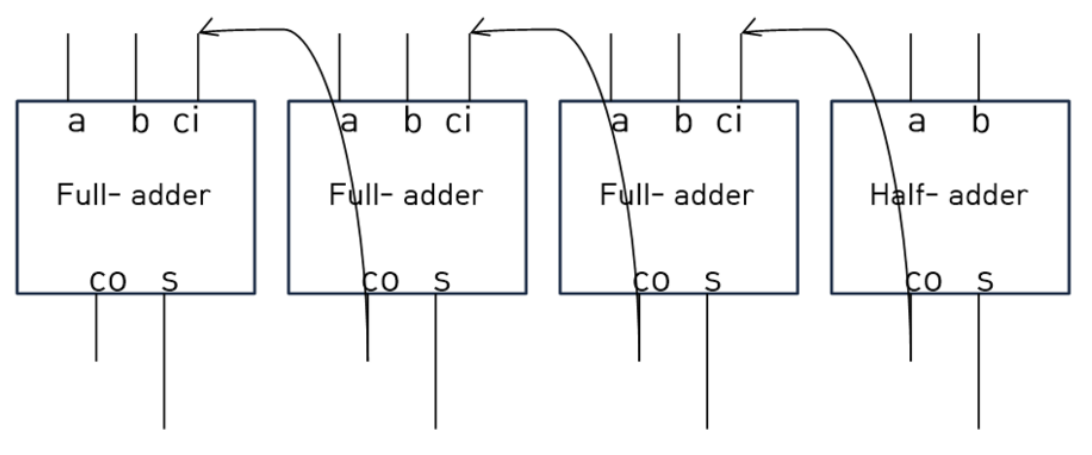
Carry-Ripple Adder
exponential 하게 자라나는 space 를 통제한다.
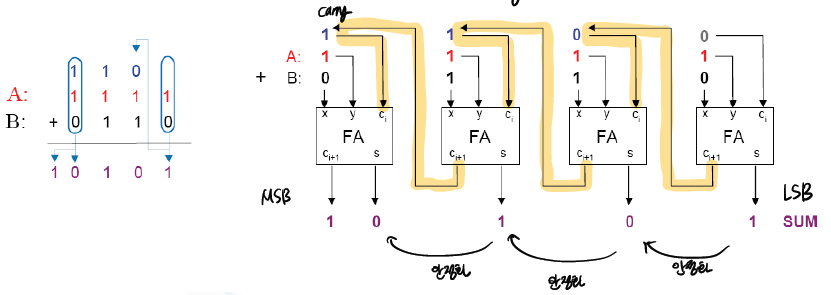
위 그림의 경우 half adder와 full adder를 합쳐 만든 adder 이다.
처음이 half adder 이기 때문에 위의 4-bit adder 로는 8-bit adder 짜리를 만들 수 없다.
하지만, half adder가 아닌 full adder를 사용한다면 ?
첫째 자리 덧셈기에서 x와 y를 더했을 때 나오는 ci+1을 옆으로 전달해준다 (노란색 하이라이트).
그걸 두번째 자리 덧셈기에 전달.. 전달.. -> 바로 전달은 안하고 안정화 후에 전달한다.
🐣 이렇게 2bit+carry 끼리의 덧셈을 하는 full adder 4개를 연결하여 4-bit 끼리의 adder 를 만들 수 있다.
⭐ ci 를 따로 적어준 이유는 범용성을 위해서 첫째 자리에 대한 carry 를 사용자에게 맞긴 것이다.
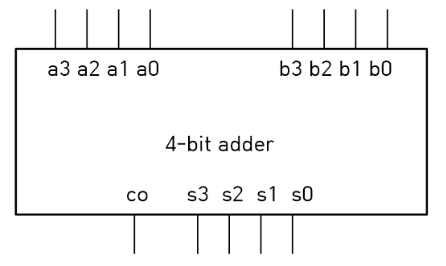
두 4-bits 를 더하면, 최대 5-bits output 이 나오고, 이때 5-bits 는 4-bits sum + 1-bit carry out 으로 구성된다.
따라서, carry-ripple adder 를 사용하면, cin 이 바깥으로 빠져나왔기 때문에 어떤 size adder던 쉽게 만들 수 있다.
하지만, LSB -> MSB 순으로 안정화가 되고, 안정화가 될 때까지 기다려야한다. full adder의 연산을 통해 carry의 값을 가지고 다음 adder 로 전달하는 방식이기 때문에 상대적으로 느리다.
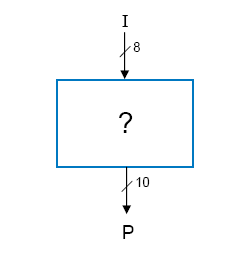
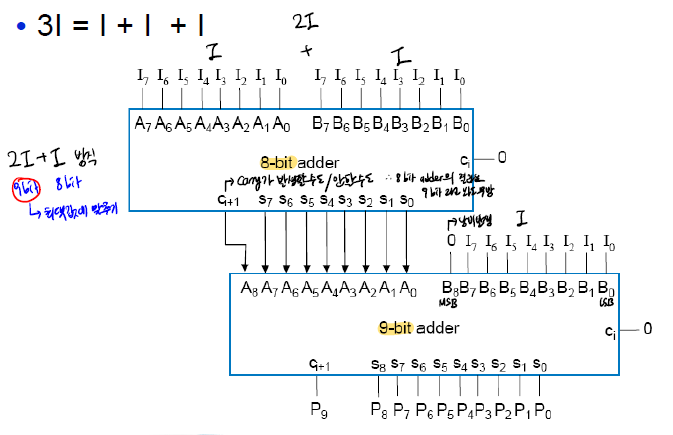
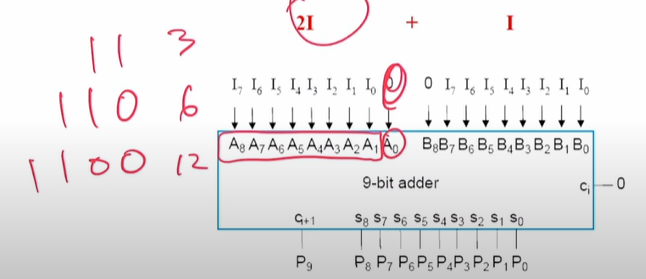
Ex1: Multiply by 3
3의 배수를 구하는 예시이다.
input: 8-bits
output: 10-bits
왜 9-bits 가 아니고 10-bits 일까?
-> 8-bits의 최대수는 1111 1111 (255) 인데, 255*3 하면 10 1111 1101 (765) 이다. log2(765) = 9.6 이므로 output이 10-bits 이다.
이렇게 하는 방법도 있으나 복잡해진다.
따라서, 아래와 같이 1-bit 를 왼쪽으로 shift 해줘서 binary 에서 정확히 곱하기 2를 가지도록 한다.
- I<<1 = I*2
Ex2: Divide by 2
2로 나누는 예시이다.
- I>>1 = I/2
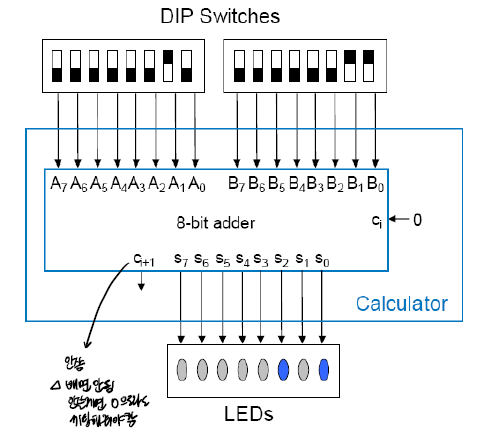
Ex3: 8-Bit Calculator
두 숫자를 DIP switches 를 통해 더한다.
결과는 8개의 LED로 표현한다.
input: 8-bit A, B
output: 8-bit sum S
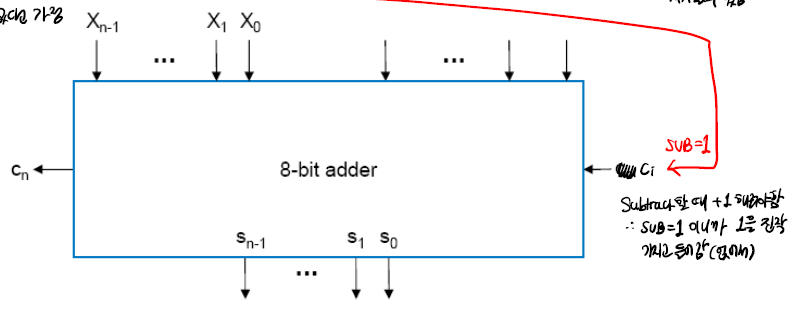
Subtraction Using Addition
- Addition: X+Y
- Subtraction: X+Y'(1의 보수)+1(2의 보수)
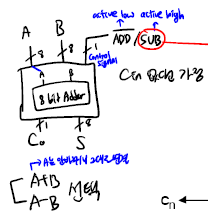
덧셈과 뺄셈 두가지 모드가 있다고 가정한다. ADD' 모드와 SUB 모드이다.
- active high: 1인 경우 동작하고, 0인 경우 동작하지 않는다.
- active low: 0인 경우 동작하고, 1인 경우 동작하지 않는다.
위 그림에서 ADD'의 경우 0을 넣으면 1이 돼서 ON 되기 때문에 active low이고, SUB의 경우 1을 넣으면 ON 되기 때문에 active high 이다.
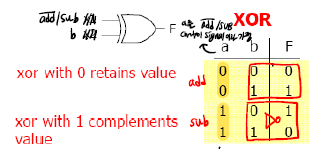
그렇다면, 이제 XOR gate 를 활용해보자.
다음 그림에서 a가 ADD'/SUB control signal 이라고 가정하고, a 자리에 ADD'/SUB 를, b 자리에는 b 를 넣어준다.
이때, ADD'의 특성을 살려서 a가 0일 때 active high (ADD') 모드가 활성화 되는 것을 알 수 있다. 만약 a가 1이면 active low (SUB) 모드가 활성화 되는 것을 알 수 있다.
특히 SUB에서 1의 보수를 사용하기 위해 NOT gate를 활용하여 뒤집어준다.
여기까지 1의 보수는 구현했는데, 2의 보수를 구현하기 위해서는 +1 을 해줘야한다. 하지만, +1 을 해주기 위해서 8-bit adder 를 추가하기엔 손해가 크므로 cin을 활용해준다.
이처럼, SUB 할 때 SUB가 1 이니까, 1을 얹고 들어가는거나 마찬가지인 것 처럼 +1을 구현해줄 수 있다.
Arithmetic Overflow
부호 있는 변수(signed variable)가 표시 할 수 있는 최대값 / 최소값을 넘어 섰을 때 부호가 바뀌면서 원하지 않는 결과가 나타나는 경우이다.
4-bits 에서 양수만 표현 시 0~15 까지, 양수+음수 표현 시 -8~7 까지 표현 가능하다.
How to determine?
c3와 c4가 다르면 overflow 가 발생하고, 같으면 overflow 가 발생하지 않는다.
부호가 다른 두 숫자를 더하면 서로 상쇄되므로 (0으로 가까워짐) magnitude 크기가 감소하는데, 이 때 overflow 가 일어날 수 없다.
⭐ c3와 c4가 다르다는 것은 부호가 같다는 뜻이고, -> oveflow
oveflow = A3B3S3' (A3, B3 음수일 때) + A3'B3'S3 (A3, B3 양수일 때)
⭐ c3와 c4가 같다는 것은 부호가 다르다는 것이다. -> x overflow
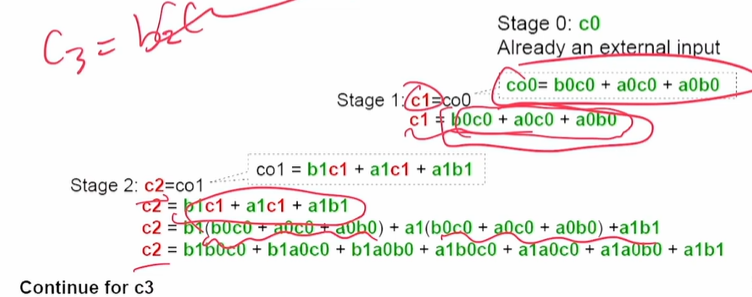
Lookahead
미리 캐리 계산해놓는 방법이다.
하지만 결국 4 bit-adder 이상으로 하기엔 한계가 있다.