15 State Encoding
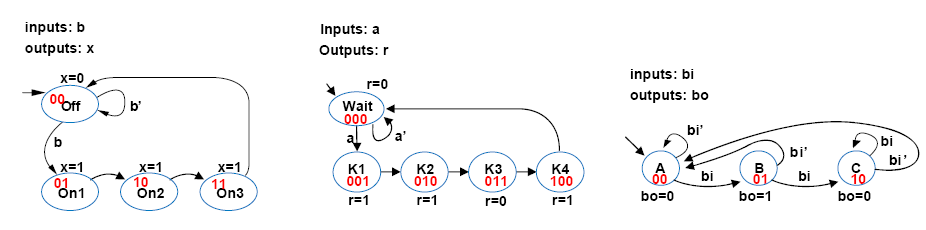
여러 경우의 수가 있을 수 있는데, 첫번째의 경우 4개의 state를 binary encoding 으로 구현했다.
두번째의 경우 5개의 state를 3개의 D-FF를 사용해서 구현했는데, 이때 don't care's 생기게 된다.
세번째의 경우 3개의 state를 2개의 D-FF를 사용해서 구현했는데, 이때도 don't care's 생긴다.
이때, 00 01 10 11 .. 등등의 순서를 11 10 01 00 순서로 해도 되고, 이때의 cost는 각각 다를 수 있다.
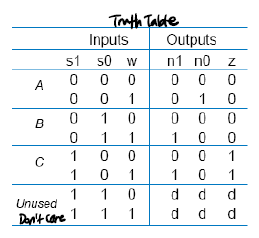
Original Minimum Bit Width Encoding
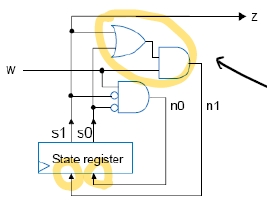
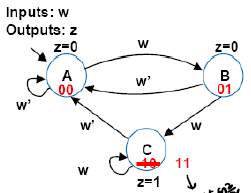
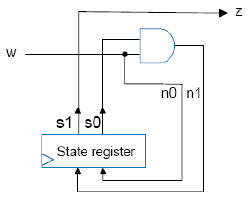
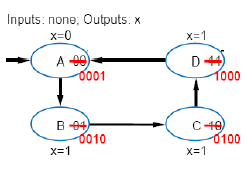
이전의 연속 1 detect 예제이다.
이 때 Cost = 3 (output 갯수) + 7 (input 갯수) = 10 이고, delay = 2 gate-delays 가 발생한다.
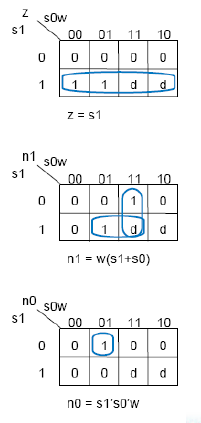
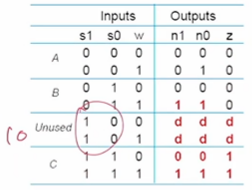
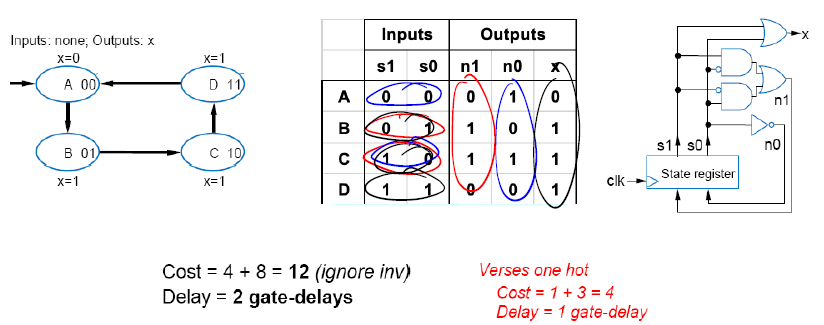
Modified Minimum Bit Width Encoding
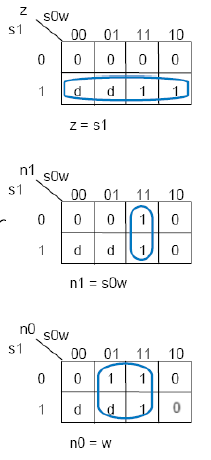
다음과 같이 don't care's 를 바꿔준다면?
훨씬 최적화가 잘 된 모습이다.
Cost = 1 (output 갯수) + 2 (input 갯수) = 10 이고, delay = 1 gate-delay 가 발생한다.
하지만, 직접 해보기 전에는 알기 어렵다.
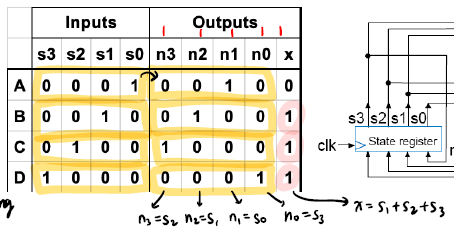
One Hot Encoding
- 간단해서 구현/디버깅 하기 쉽다.
- don't care's 많이 생겨서 k맵 상에서 최적화 할 room이 생기기 때문에 combination logic이 간단해진다.
- FF가 남아도는 경우
- 하지만 state 개수가 많아질수록 FF개수가 늘어나므로 실용적이지 않다.
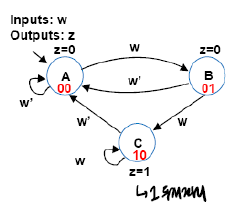
s0일 때, n1으로 가고, s1일 때, n2로 가고 .. 이런 패턴으로 진행된다.
결과 x는 s1+s2+s3 일 때가 된다.
그리고, Cost = 1 + 3 = 4 가 되고, Delay = 1 gate-delay 가 된다.
다음은 binary encoding 으로 구현한 것이다.
복잡하게 꼬여서 cost가 증가한다.
Problem
일단 binary encoding 해보고, 랜덤으로 해보고, 감으로 해본다.
❗ 하지만, 너무 어려워서 제대로 풀 방법이 없다. -> Intractable problem