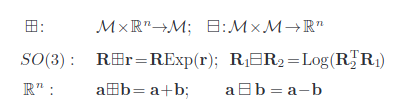
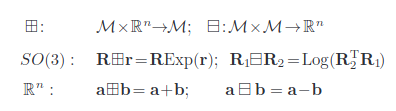
현재 feature를 뽑는 방법에 대해 공부하고 있는데 최근(?) 알고리즘 중 raw data를 쓰는
FAST-LIO2는 왜 feature를 뽑지 않는지 뽑지 않고 어떻게 효율적으로 작업을 수행하는지 궁금하여 이 논문을 읽게 되었습니다.
이 논문은 2022 T-RO에 나왔고 FAST-LIO의 후속 논문입니다.
FAST-LIO에 대해 간단히 소개하자면
IMU data를 활용하여 motion distortion을 제거하고
iterated Kalman filter를 활용하여 odometry and mapping을 진행하는 알고리즘입니다.
이 filter를 사용하면 Kalman gain을 계산하는데 많은 시간이 걸리는데 계산이 쉬운 Kalman Gain을 도입하여 계산속도를 높였습니다. 혹시 다음에 더 자세하게 소개할 시간이 있으면 다뤄보도록 하겠습니다.
FAST-LIO2로 돌아와서 이 논문에 대해 소개하겠습니다.
1. Introduction
이 논문에서는 LiDAR Odometry and mapping의 4가지 도전과제가 있다고 말합니다.
1) 많은 point를 로봇에 내장되어 있는 컴퓨터에서 계산할 수 있어야한다.
2) Feauture는 LiDAR Senesing type과 주변 환경에 영향을 받는 단점이 있다.
3) 보통 LiDAR sensor를 계산할 때 sampling을 하는데 이것은 motion distortion을 야기한다.
4) LiDAR는 낮은 resolution을 가지고 있어서 dense한 map을 만들기 힘들다.
이 문제들을 해결하기 위해 FAST-LIO2는 다음과 같은 해결책을 제시합니다.
1) k-d tree의 발전 버전인 ikd-tree를 활용하여 많은 dense point를 다룰 수 있도록 한다.
2) ikd tree로 계산속도가 빨라졌기 때문에 feature를 뽑지 않고 raw data를 사용한다.
3) FAST-LIO에서 제안된 tightly coupled fusion형식과 iterated kalman filter형식을 사용한다.
2. Overview
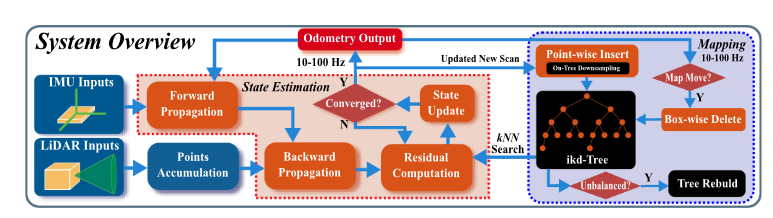
fast-lio2는 10ms~100ms동안 sampling된 raw data를 축적합니다.
축적된 data는 scan으로 부르며 state estimation을 하기위해 point들은 iterated kalman filter를 통해 유지되는 map point에 등록되게 됩니다. Global map point들은 ikd-tree에 정렬됩니다. ikd-tree에서 옛날 데이터는 적절하게 삭제한 후 residual을 계산하는데 사용됩니다.
이런식으로 최적화된 pose들은 포인트들을 등록하고 그것들을 map에 병합하게 됩니다.
3.Sate Estimation
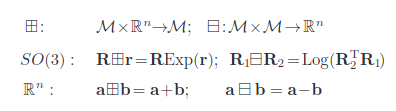
이 논문에서는 서로 다른 코디네이트 계산을 한꺼번에 하기 위해 box plus, minus라는 개념을 사용합니다. 그냥 더하고 뺀다고 생각해도 무방합니다.
A. Kinetic Model
1) State Transition Model
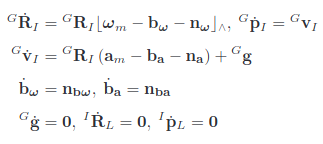
P는 IMU postion을 의미하고 R은 IMU attitude를 의미합니다. g는 중력 가속도, b는 IMU bias이고 n은 noise입니다. 왼쪽 위에 표지된 G는 frame을 나타내고 global frame이란 것을 말해주고 있고 I는 IMU frame을 의미합니다.
이 continuous state transition model은 IMU sampling을 통해 discretize가 됩니다.

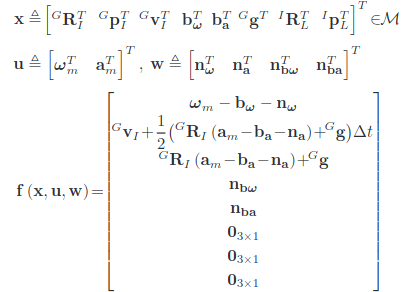
이런 식으로 IMU data를 업데이트하게 됩니다.
FAST-LIO와는 다르게 extrinsic parameter인 imu frame R과 P를 도입하여 online으로도 추정할 수 있게 하였다고 합니다.
2) Measurement Model
LiDAR가 움직이면서 주변 환경은 관측하기 때문에 다른 pose에서의 point들이 관측됩니다.
이 논문에서는 이것을 하나의 pose로 만들어주기 위해서 backpropagation 과정을 진행합니다.
이 과정을 통해 point들이 scan이 끝나는 시점의 pose에서 동시에 관측된 것으로 계산할 수 있습니다.
noise를 제거하고 끝나는 시점으로 projection된 point를 활용하여 measurement model을 정의합니다.
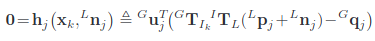
u는 corresponding plane의 normal vector입니다.
B. Iterated Kalman Filter
앞 서 manifold M에서 정의한 state model과 measurement model을 기반으로 iterated Kalman filter를 사용할 것입니다.
1) Propagation
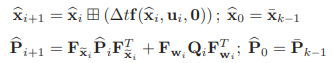
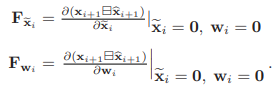
state와 covariance는 이 수식에 따라 propagation을 진행합니다.
state는 noise가 0으로 가정하였고 covariance는 covariance propagation을 활용합니다.
2) Residual Computation
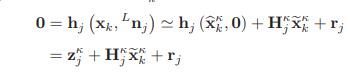
measurement model을 first order approximation을 적용하고 iteration x를 삽입하여 간단화할 수 있습니다.
여기서 z가 residual이고 r은 noise입니다.
residual을 좌변에 오도록 정리하면
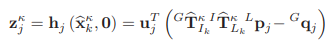
이 식이 나오게 되고 residual을 계산할 수 있게 됩니다.
3) Iterated Update
IMU state error:
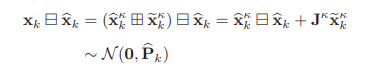
LiDAR state error:
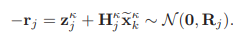
이 두 error를 활용하여 최적화 term을 만들 수 있습니다.
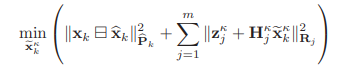
이러한 MAP 문제는 iterated Kalman Filter를 사용하여 해결할 수 있습니다.
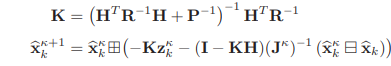
보통의 measurement dimension역행렬을 구해야하는 kalman gain과 달리 state dimension을 활용하여 계산량을 줄였습니다. 이 iteration을 통해 수렴하면 새롭게 pose를 estimation하여 LiDAR point를 구한 후 ikd-tree로 정렬된 map point에 넣습니다.
요약: iterated Kalman filter를 활용하여 state를 추정합니다.
이때 kalman filter의 단점인 과도한 계산량을 해결하기 위해 계산 때 이용하는 dimension을 바꾸었습니다. 이후 mapping 과정에서 optimization하도록 map point에 등록을 합니다.
4.MAPPING
A. Map Management
Map point는 ikd-tree에 정렬됩니다.
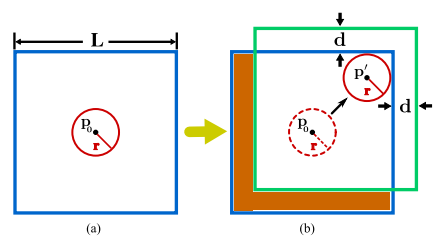
Map이 너무 커지는 것을 막기 위해 한 변의 길이가 L인 사각형에 map point를 정렬합니다.
LiDAR를 중심으로 detection ball을 만들고 이 detection ball이 사각형의 한 변에 닿게 되면 닿은 변의 방향으로 사각형을 거리 d만큼 움직이고 이동하여 사각형 안에 들어있지 않게 된 point들은 삭제시키면서 map을 유지하게 됩니다.
B. Tree Structure and Construction
1) Data Structure

Point: point coordinate, intensity와 같은 point 정보
Treesize: 기준 point부터 시작되는 tree의 모든 point 개수
axis: 공간을 나누는 axis
treedeleted: 삭제된 node
invalidnum:삭제된 point의 개수
range: 유효한 point를 갖고있는 cuboid의 범위
2) Structure
kd tree와 마찬가지로 가장 긴 dimension을 나눌 수 있게 구조화합니다.
C. Incremental Updates
ikd tree를 어떻게 업데이트하는지 알아보겠습니다.
업데이트에는 boxwise operation, pointwise operation이라는 2가지 주요한 operation이 있습니다.
pointwise operation은 kd-tree와 마찬가지로 point 하나를 insert,delete,re-insert합니다.
boxwise operation은 cuboid에 정렬된 모든 point들을 insert,delete,re-insert합니다.
1) Point Insertion with on-tree downsampling:
공간을 균등하게 나눌 수 있는 길이 l을 한변으로 하는 큐브 Cd를 정의합니다.
처음 Search에서는 Cd에 포함되어 있는 모든 point와 새로운 point를 point array V에 넣습니다. 그 후 V안에서 center point와 가장 가까운 점을 찾은 후 나머지 point들은 모두 제거합니다. 가장 가까운 point는 k-d tree에 저장됩니다. 이를 통해 LiDAR point를 Sampling할 수 있습니다.
이렇게 sampling된 point들은 이러한 형태로 tree를 내려가 빈 노드에 저장됩니다.
내려가는 과정에서 원래 있던 node의 정보들도 업데이트되게 됩니다.

2)Boxwise Delete Using Lazy labels
이 tree의 delete 과정에서는 lazy delete strategy를 사용합니다.
이것은 삭제된 point들이 node에서 바로 제거되지 않고 deleted값만 True로 변경됩니다.
만약 sub-tree의 모든 node들의 deleted 값이 True가 된다면 treedeleted값이 True로 변경됩니다. 이렇게 설정된 lazy label들은 tree rebuilding 과정을 통해 제거되게 됩니다.
Boxwise Delete는 다음 그림과 같이 보면 조금 이해가 편합니다.
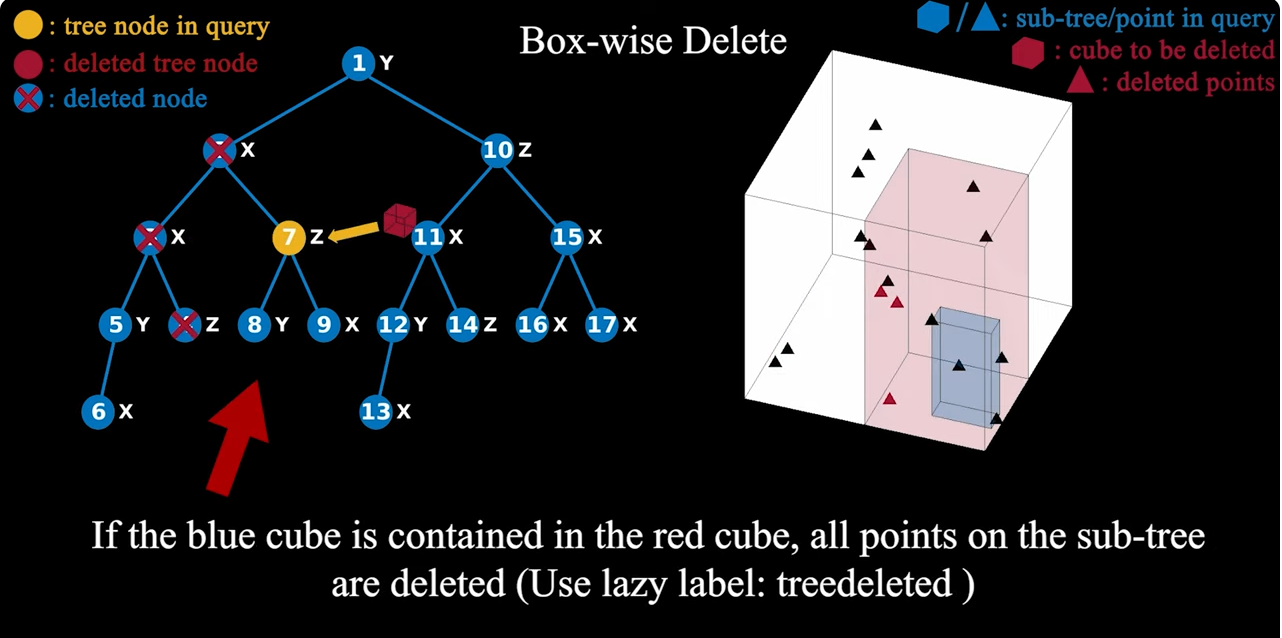
point는 자신에게 할당된 공간이 있고 그 공간이 모두 delete box에 들어가게 된다면
자신 밑의 모든 point는 확인하지 않고 제거 label을 붙일 수 있습니다. 이렇게 tree 탐색의 시간을 줄일 수 있게 됩니다.
=> 이 논문에서는 Point insertion과 Boxwise Delete만 설명하였지만 pointwise operation, boxwise operation에 insertion delete reinsertion 모두 존재합니다.
D.Rebalancing
1) balancing criterion
ikd-tree에선 balance를 두가지로 정의합니다.
이것은 알파 balance criterion입니다.
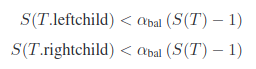
S(T)는 T point부터의 treesize입니다. 이것을 만족해야 alpha balance criterion을 만족하는 것입니다.
두번째로는 alpha delete criterion입니다.
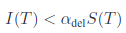
I(T)는 tree에 있는 invalidNum입니다. 이것을 만족하면 alpha delete criterion을 만족하는 것입니다.
두 기준을 모두 충족하여야 tree가 균형잡힌 것이고 이것이 깨진다면 rebuilding 과정을 겪게 됩니다.
2) Rebuild and Parallel Rebuild
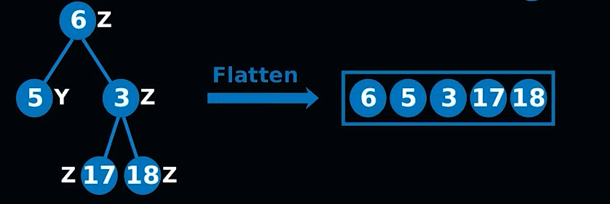
balance가 깨진 tree는 vector V로 flatten되어 다시 정렬됩니다.
이 과정에서 delete label이 True인 point가 제거됩니다.
하지만 만약 balance가 깨진 tree의 크기가 크다면 연산량이 많아 질 것이기 때문에
이 논문에선 double-thread rebuilding method를 사용합니다.

이것은 rebuilding 해야하는 tree의 크기가 일정 이상 클 경우
tree를 복사해가서 따로 rebuilding 작업을 진행한다. 그 동안 tree에서 들어오는 데이터를 저장해놓고 있다가 rebuilding이 완성되면 새로운 tree에 다시 등록하게 됩니다.
E. K-nearest Neighbor Search
ikd-tree에서는 k-nearest Neighbor Search를 다르게 최적화하여 진행한다.
원래 k-nearest Neighbor Search는 가장 작은 k개의 point를 찾고 가장 먼 point와의 거리를 구하는 것인데 ikd-tree에서는 Cuboid Ct와의 가장 가까운 거리를 갖고 있고 그 거리와 가장 먼 point의 거리를 비교하여 계산할 point를 걸러냅니다.
5. Conclusion
FAST-LIO2는 iterated Kalman filter를 사용하여 IMU와 LiDAR를 tightly-coupled fusion하여 정확한 State를 구할 수 있었습니다. FAST-LIO1 에서 사용한 것 처럼 Kalman Gain의 dimension을 바꿔 훨씬 효율적으로 계산하게 하였고 map에 point를 할당하는 것은 ikd-tree구조를 사용하여 빠르게 다룰 수 있도록 하여 filter based SLAM의 단점인 속도를 보완하였습니다.
