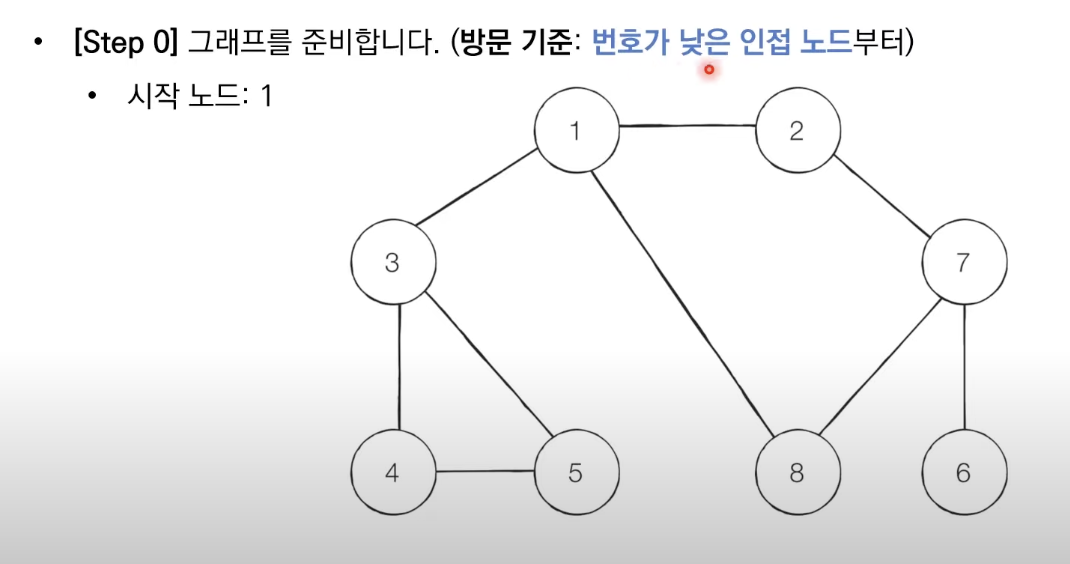
그래프 탐색 알고리즘
많은 양의 데이터 중 원하는 데이터를 찾는 과정을 탐색이라 한다.
대표적인 그래프 탐색 알고리즘은 DFS와 BFS가 있다. 두 유형 모드 코딩 테스트에서 매우 자주 등장하는 유형 이라고 한다.
스택 자료구조
- 먼저 들어온 데이터가 나중에 나가는 형식의 자료구조. First In Last Out
- 파이썬에선 append()와 pop()메서드의 형태.
- ex) 삽입5 - 삽입2 - 삽입3 - 삽입7 - 삭제 - 삽입1 - 삽입4 - 삭제
큐 자료구조
- 먼저 들어 온 데이터가 먼저 나가는 형식(선입선출)의 자료구조.
- 파이썬 에서는 deque라이브러리의 append()와 popleft로 구현 할 수 있다.
- 리스트 자료형을 이용해 큐구현 가능하지만 시간 복잡도 측면에서 덱 라이브러리를 사용하는것이 유리하다.
- ex) 삽입5 - 삽입2 - 삽입3 - 삽입7 - 삭제 - 삽입1 - 삽입4 - 삭제
재귀함수(유클리드 호제법)
두개의 자연수에 대한 최대공약수를 구하는 대표적인 알고리즘으로는 유클리드 호제법이 있다.
두자연수 a, b에 대하여(a>b)를 b로 나눈 나머지를 r이라고 하자.
이때 a와 b의 최대 공약수는 b와 r의 최대공약수와 같다.
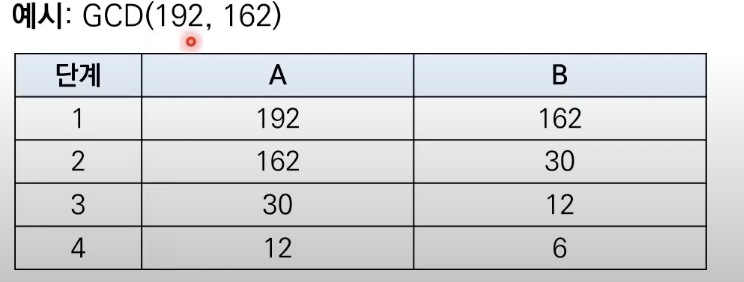
최대공약수란?
정수의 성질 중 하나. 초등학교 5학년 때 나오며, 약수(divisor or factor)에 대해서 먼저 배운 뒤, 바로 배우게 될 것이다. 먼저 공약수(common divisor or common factor)란, 이름에서 알 수 있듯이 두 수, 혹은 그 이상의 여러 수의 공통인 약수라는 뜻이다. 최대공약수 (greatest common divisor) 는 당연히 공약수 중 가장 큰 것. 두 수 a,ba,b의 최대공약수를 수학적 기호로 표시하면, \gcd\left(a,b\right)gcd(a,b)이며,[1] 더욱 줄여서 \left(a,b\right)(a,b)로 표기하기도 한다.[2] 특히, \gcd\left(a,b\right)=1gcd(a,b)=1이면 두 수 a,ba,b는 서로소(relatively prime, coprime)라고 한다.
def gcd(a, b):
if a % b == 0:
return b
else:
return gcd(b, a % b)
print(gcd(192, 162))
# 결과 6DFS(Depth-First Search)
DFS는 깊이 우선 탐색이다. 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
DFS 예제
DFS는 스택 자료구조(혹은 재귀함수)를 이용하며, 아래와 같이 동작한다.
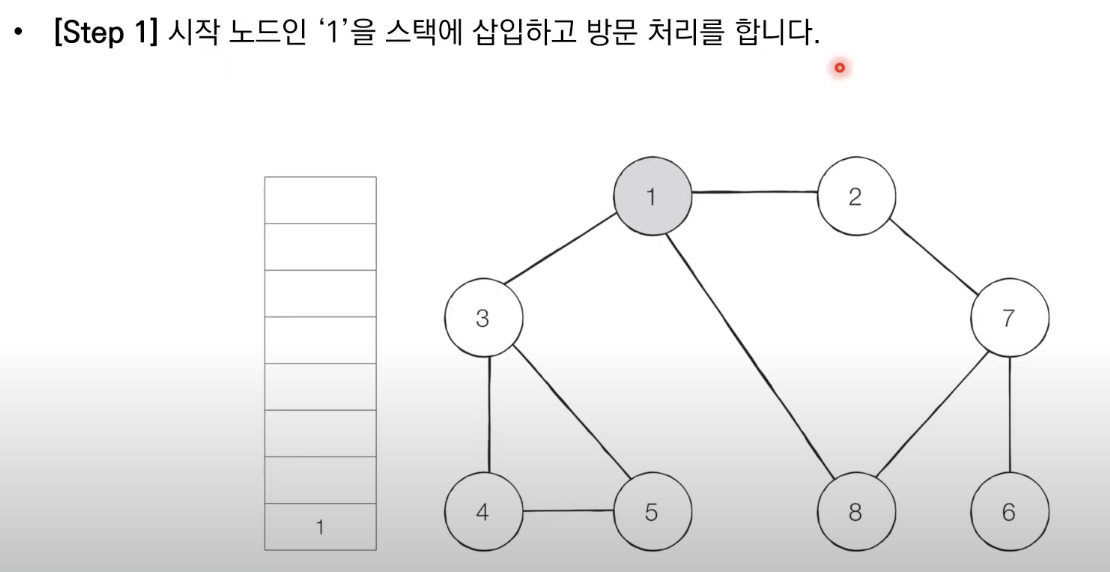
1. 탐색 시작 노드를 스택에 샆입하고 방문 처리를 한다.
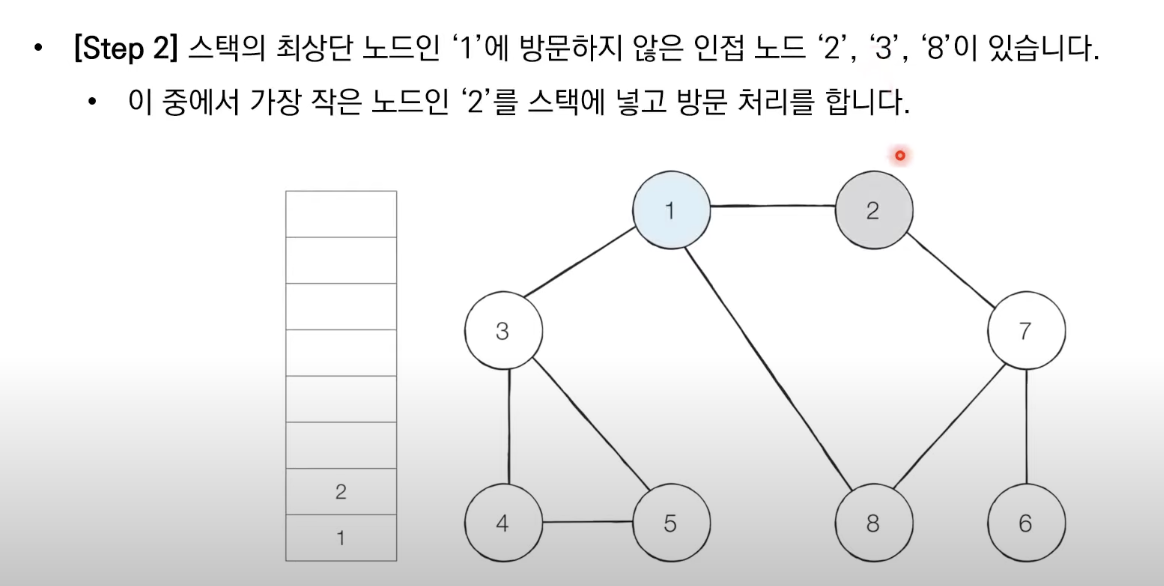
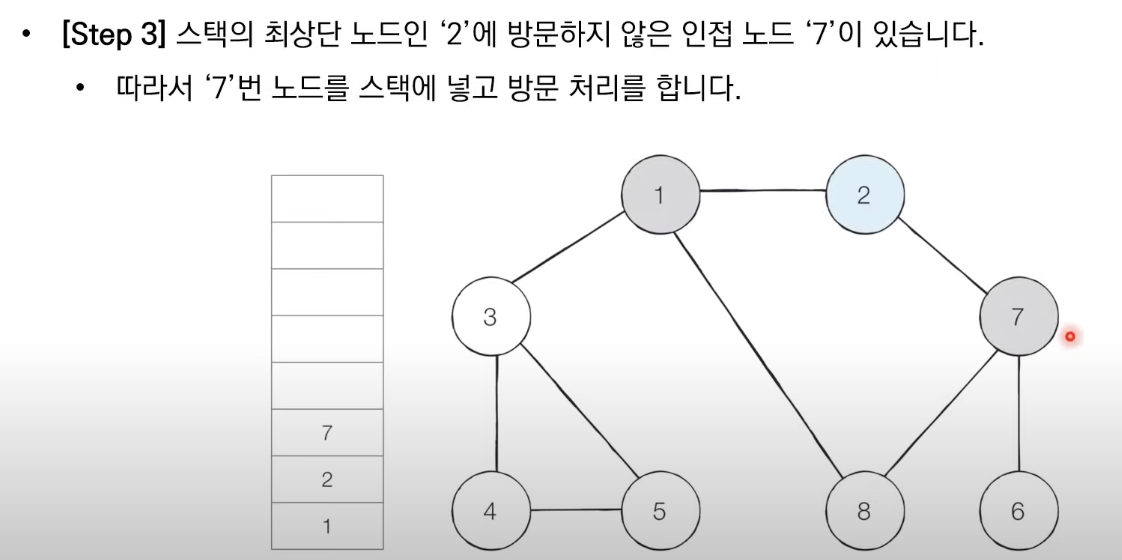
2. 스택의 최상단 도느에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 더이상 2번의 과정을 수행할 수 없을 때가지 반복한다.
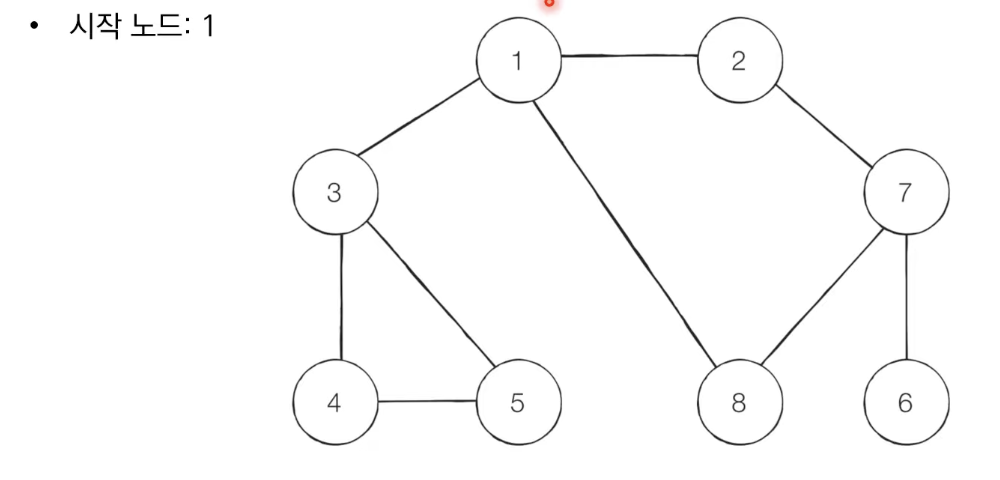
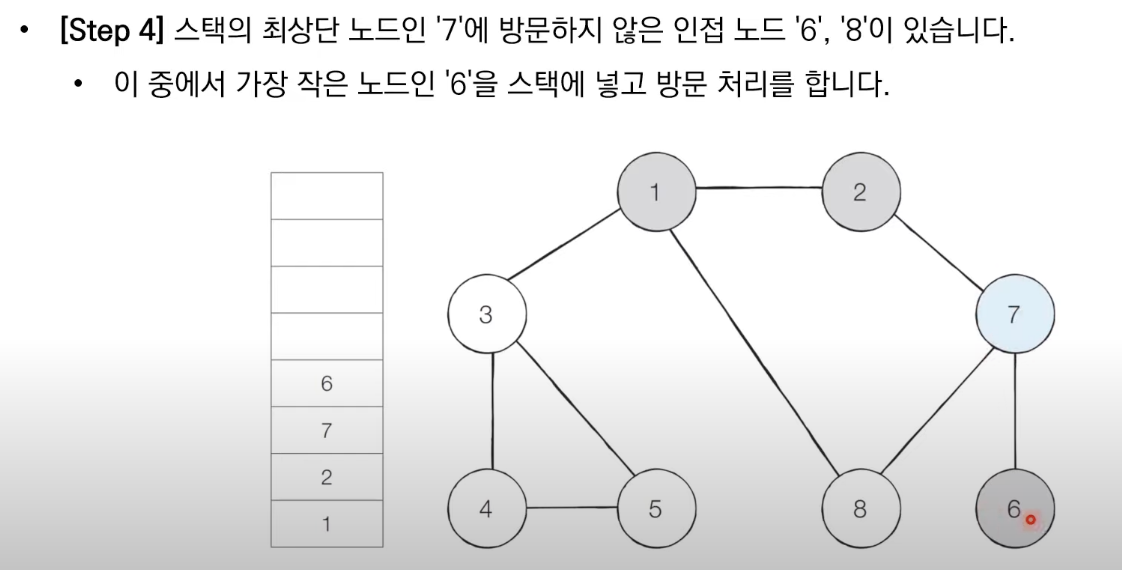
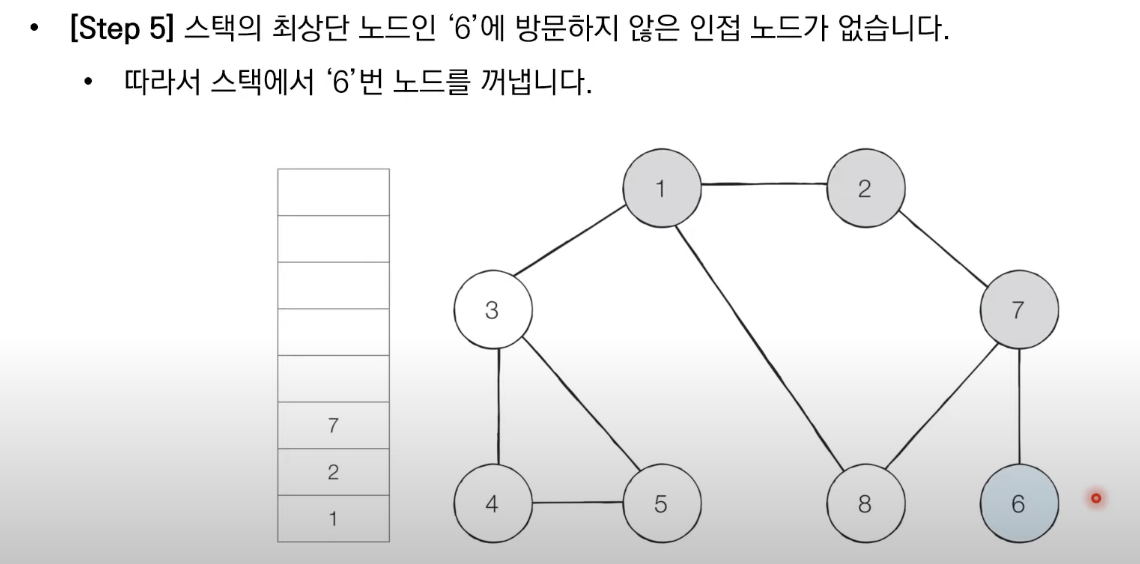
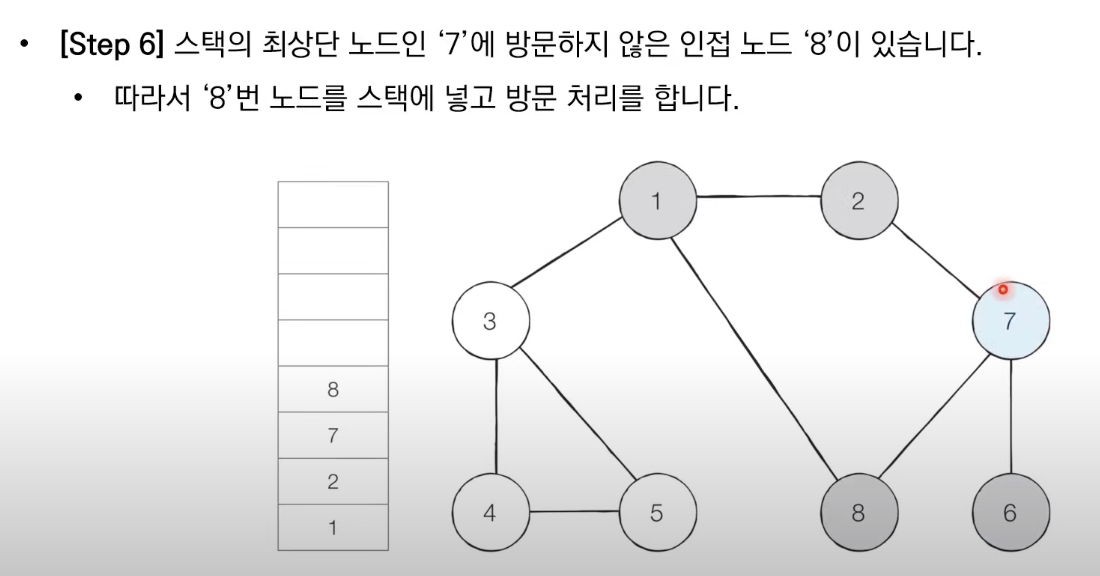
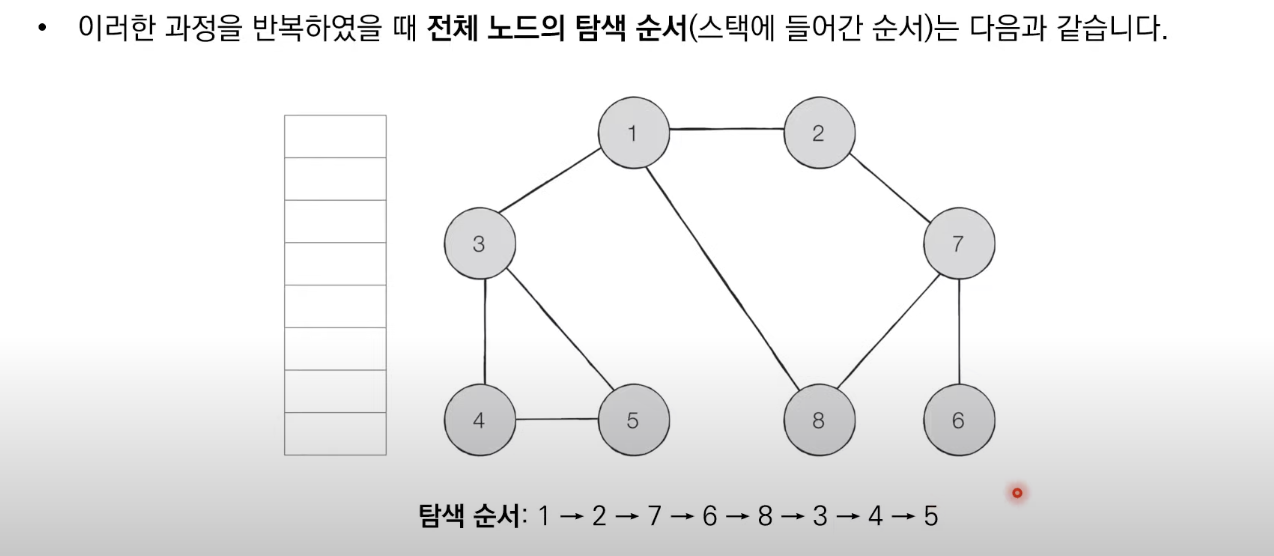
def dfs(graph, v, visited):
visited[v] = True
print(v, end='')
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
dfs(graph, 1, visited)'''
시작 dfs(graph, 1, visited)
visited[1] = True로 만들고 1을 출력한다
graph[1] = [2,3,8]리스트를 반복한다.
i = 2 if not visited[2] 는 True
[False, True, False, False, False, False, False, False, False]
def(graph, 2, visited)
visited[2] = True로 만들고 2를 출력한다.
[False, True, True, False, False, False, False, False, False]
graph[2] = [1, 7] 리스트를 반복.
visited[1]은 True기 떄문에 조건문 건너뛰고
7은 False로 dfs(graph, 7, visited)
visited[7] = True로 만들고 7을 출력한다
[False, True, True, False, False, False, False, True, False]
graph[7] = [2, 6, 8] 리스트 반복.
visited[2] = True로 다음루프
visited[6] = False로 dfs(graph, 6, visited)
visited[6]을 True로 만들고 6을 출력
.....
'''DFS 예제: 음료수 얼려 먹기
DFS로 풀어본 예제를 첨부한다. 머리가 좋은편이 아니라 반복문과 기타 로직을 하나하나 써가며 이해한 문제이다. 처음엔 방문 처리라는 표현 때문에 혼돈이 있었지만 반복해서 보다보니 이해할 수 있었다. 0으로 되어있는 곳을 모두 방문하면서 결과값을 1올려주면 해결 가능한 문제였다.
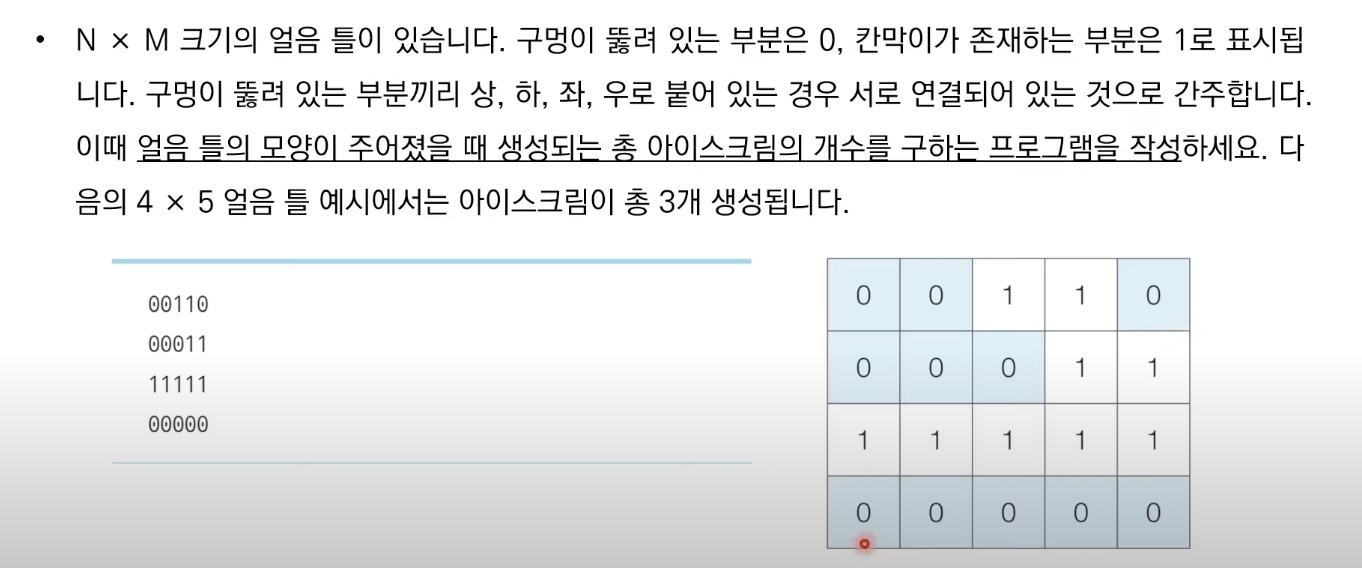
n, m = map(int, input().split())
graph = []
for i in range(n):
graph.append(list(map(int, input())))
def dfs(x, y):
# 범위 확인
if x <= -1 or x >= n or y <= -1 or y >= m:
return False
# 얼릴 수 있는 곳인지 확인후 방문처리
if graph[x][y] == 0:
graph[x][y] = 1
dfs(x - 1, y)
dfs(x, y - 1)
dfs(x + 1, y)
dfs(x, y + 1)
return True
return False
result = 0
for i in range(n):
for j in range(m):
if dfs(i, j) == True:
result += 1
print(result)모든 과정은 너무 기니 결과 값이 처음 1으로 변경되는 부분만 작성한다.
# 초기 그래프
[
[0, 0, 1, 1, 0],
[0, 0, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0]
]
# for 문에서 dfs(0, 0)을 호출
[
[1, 0, 1, 1, 0],
[0, 0, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0]
]
# graph[0][0] 을 방문처리하고
# dfs(0,0)안의 재귀 시작
# dfs(-1, 0),dfs(0, -1)->Fasle 함수종료
# dfs(0,0)안의 재귀 dfs(x+1,y)
# dfs(1,0)은 방문전 -> 1로 바꾸어 주고
[
[1, 0, 1, 1, 0],
[1, 0, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0]
]
# dfs(1,0)의 재귀 시작
# dfs(1-1, 0)은 위에서 1로 방문 처리함 False로 종료
# dfs(1, -1)False로 종료
# dfs(2, 0)False로 종료
# dfs(1,1)-> 방문전 -> 1로 바꾸어주고 재귀 시작
[
[1, 0, 1, 1, 0],
[1, 1, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0]
]
# dfs(x-1, y)는 dfs(0, 1)로 방문전 노드 -> 방문처리후 재귀 시작
[
[1, 1, 1, 1, 0],
[1, 1, 0, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0]
]
# dfs(0, 1)안쪽의 재귀 dfs(-1, 1), dfs(0, 0),
# dfs(1, 1), dfs(0,2)모두 False True반환 하면서 dfs(0,0)안의 dfs(1, 0) 안의 dfs(1, 1) 안의 dfs(0, 1)재귀 종료
# dfs(1,1)의 dfs(x, y-1)로 돌아온다 dfs(1,0)은 방문 False로 함수종료
# dfs(x + 1, y) -> dfs(2, 1) False
# dfs(x, y + 1) -> dfs(1, 2) 방문처리 재귀 시작
[
[1, 1, 1, 1, 0],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 0, 0, 0]
]
# dfs(1,2) 재귀는
# dfs(0, 2), dfs(0, 1), dfs(2, 2), dfs(1, 3)로 모두 False
# dfs(0,0)안의 dfs(1, 0) 안의 dfs(1, 1) 안의 dfs(1,2)재귀 종료 True 반환 후 함수 종료
# dfs(1,1)도 True 반환 후 종료
# dfs(0, 0) 안의 dfs(1, 0)종료
# dfs(0, 0) 안의 dfs(0, 1)시작
# dfs(0, 1) 은 false 함수종료
# dfs(0, 0)의 모든 재귀함수가 끝났고 True를 반환하고 종료
# for 문에서 result +=1
# dfs(0, 1) 시작BFS(Breadth-First-Search)
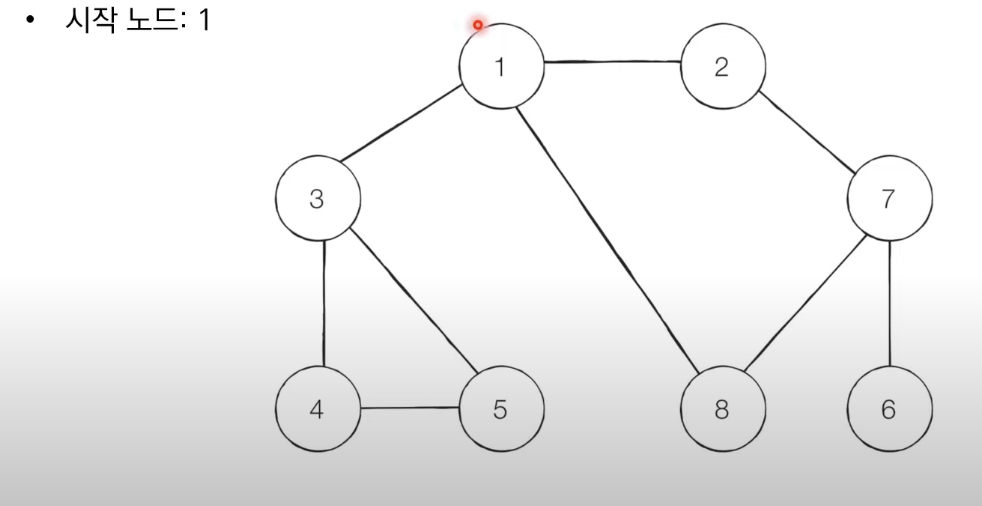
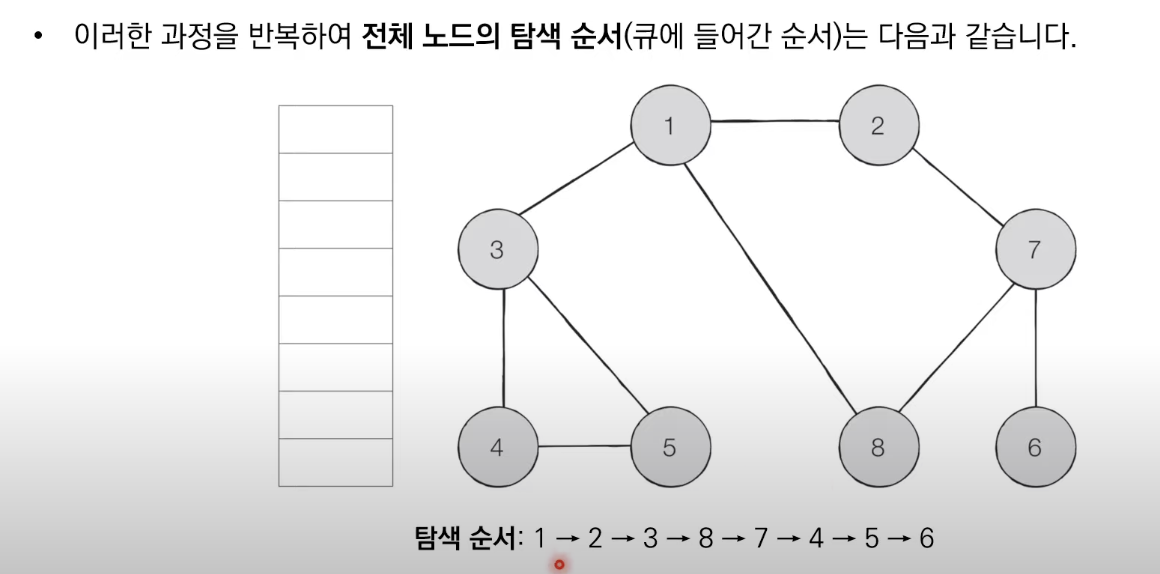
BFS는 너비 우선 탐색이다. 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘 이다.
BFS 예제
BFS는 큐 자료구조를 이용하며 아래와 같이 동작한다.
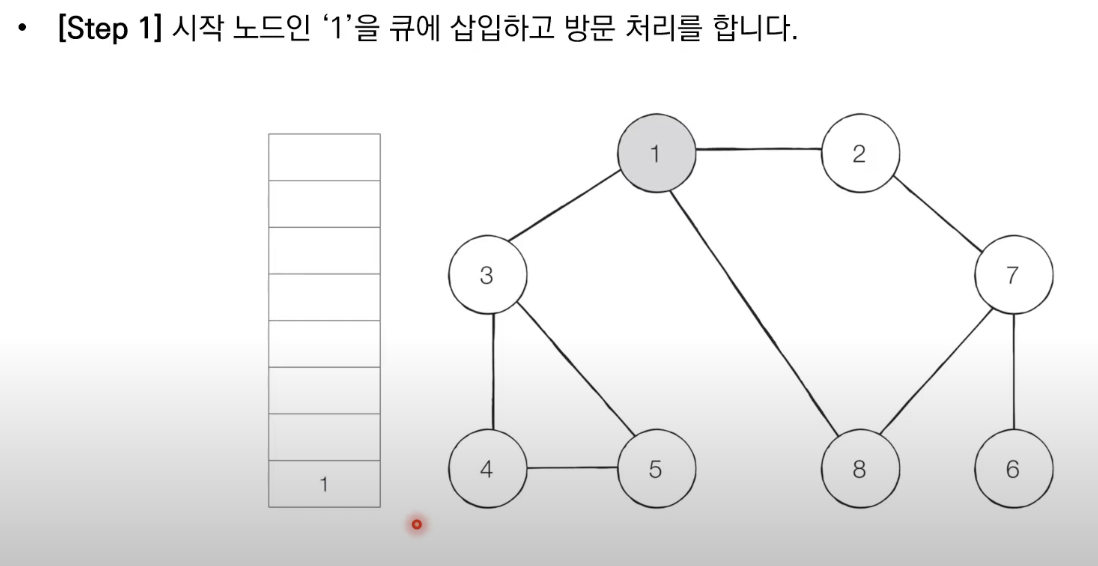
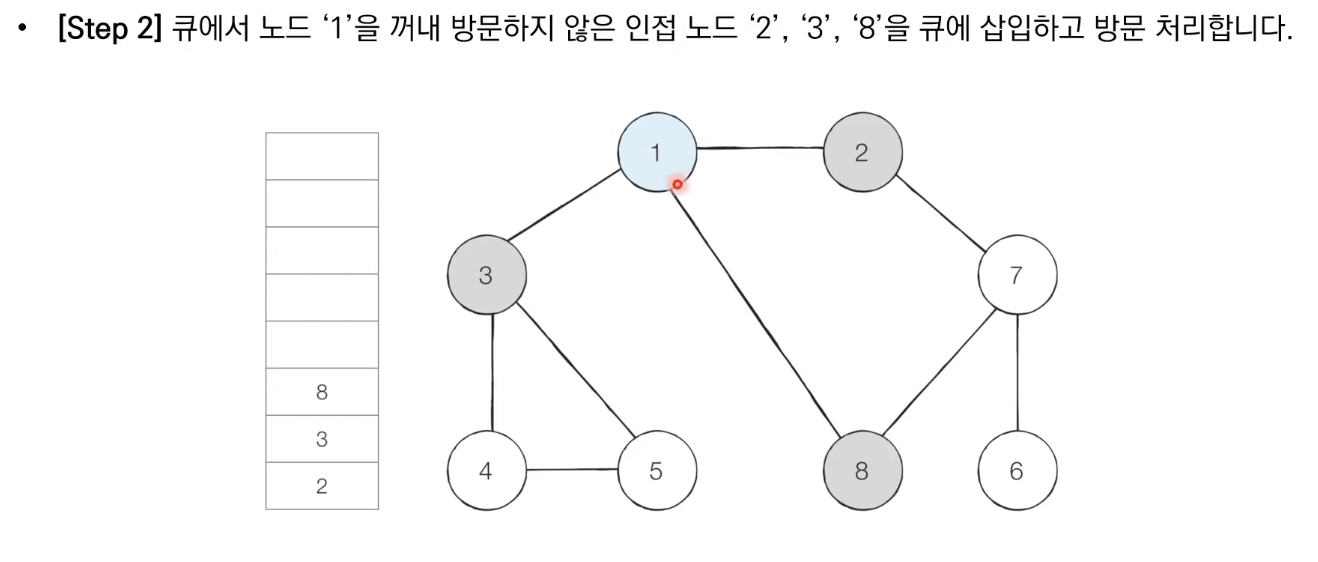
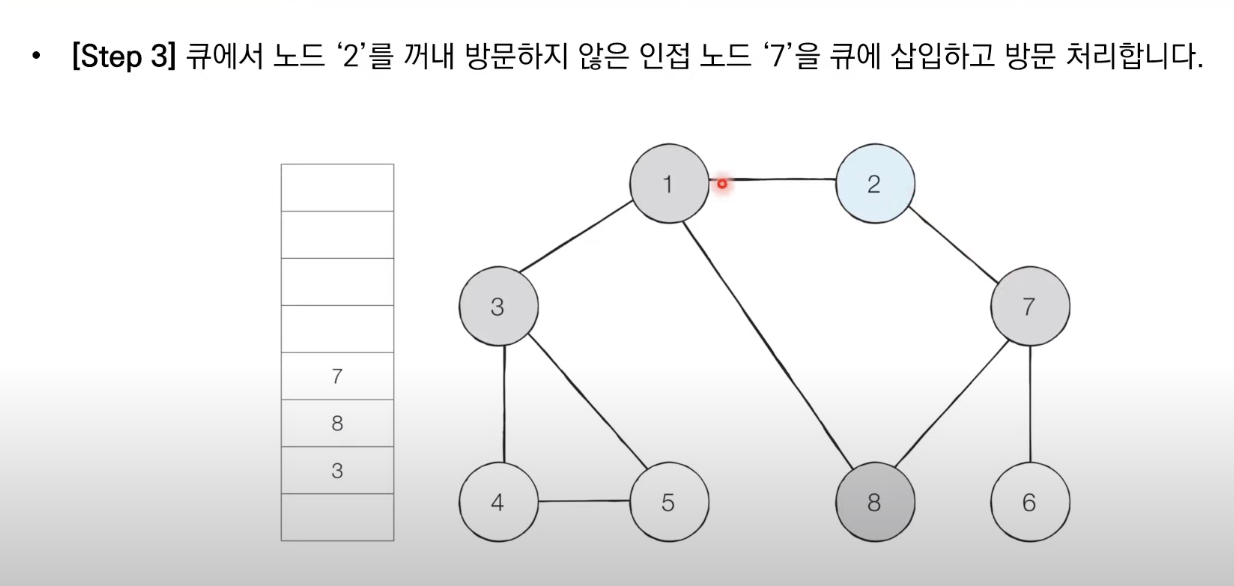
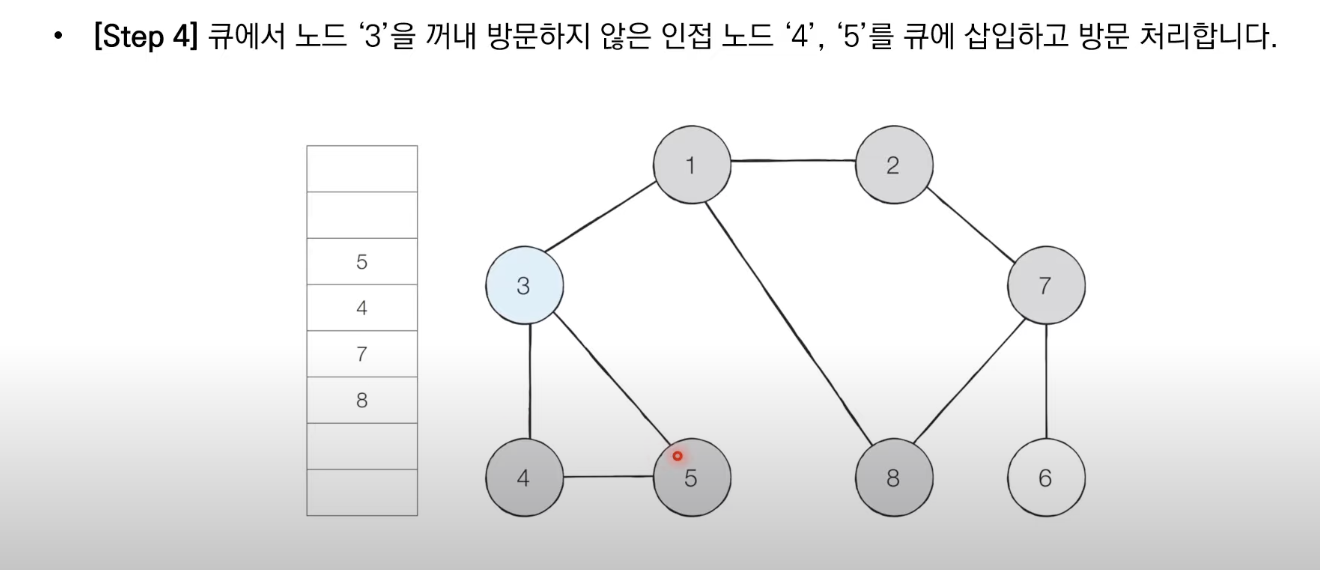
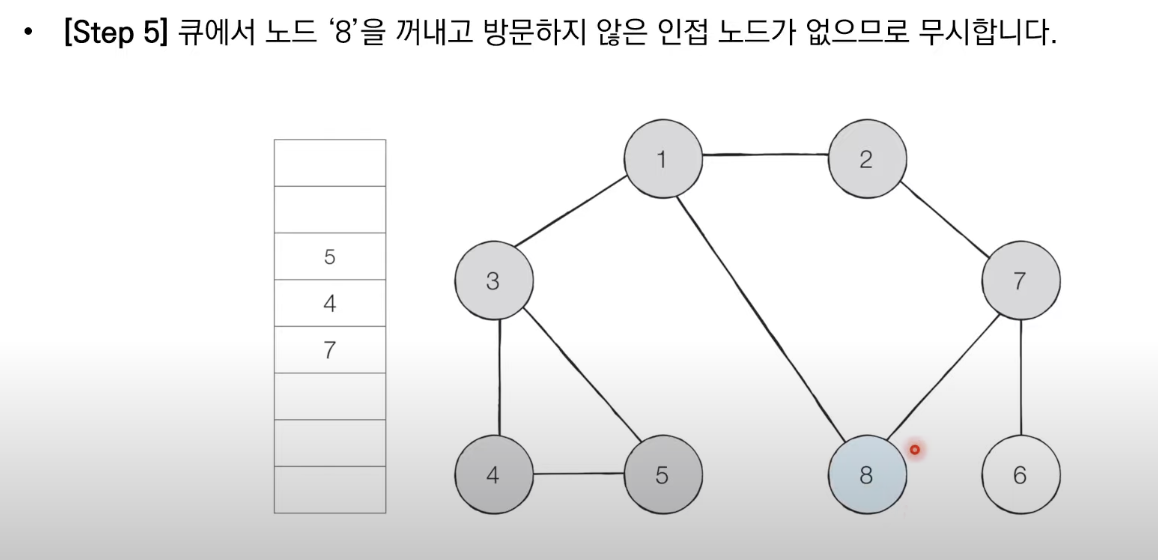
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.
from collections import deque
def bfs(graph, start, visited):
queue = deque([start])
visited[start] = True
while queue:
v = queue.popleft()
print(v, end='')
for i in graph[v]:
if not visited[i]:
queue.append(i)
visited[i] = True
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
bfs(graph, 1, visited)BFS 예제: 미로 탈출
이예제는 처음 풀려고 할때 각 리스트를 반복하면서 비트 연산으로 풀 수 있을거 같았다. 이번 주제는 BFS이기 때문에 해당 알고리즘으로 풀었다.
이문제는 최소 값을 구하는 문제로 새롭게 방문하는 노드의 값을 1씩 증가시키면서 진행하면 문제를 해결 할 수있다.

# deque
from collections import deque
n, m = map(int, input().split())
graph = []
for i in range(n):
graph.append(list(map(int, input())))
# 이동할 방향 정의 (상, 하, 좌, 우)
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
def bfs(x,y):
queue = deque()
queue.append((x,y))
while queue:
x, y = queue.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx == 0 and ny == 0 or nx < 0 or nx >= n or ny < 0 or ny >= m:
continue
if graph[nx][ny] == 0:
continue
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1
# 큐에 현재 인덱스 값을 넣어 다시 탐색한다.
queue.append((nx, ny))
return graph[n - 1][m - 1]
print(bfs(0, 0))이문제 역시 전체 해설은 너무길기 때문에 이미 방문한 노드를 건너뛰고 다음 노드로 진행하는 부분만 기록하겠다.
# 출발 위치가 (0, 0)으로 함수 bfs에 x, y로 들어간다
# 큐 객체에 (0, 0)이 추가 되고
# while 반복문 에서 queue객체에서 x,y를 꺼내고
# 위에 정의해놓은 방향 벡터를 이용해 인접한 노드를 확인한다.
# 노드의 값이 범위에 해당하지 않거나 0 즉 괴물이 있는곳 이라면
# continue로 다음 루프를 진행한다.
# 인덱스에 해당하는 노드가 1로 이동 가능한 노드라면
# 해당 노드의 값을 1 증가시킨후 큐 객체에 해당 인덱스를 추가한다.
"""
시작 큐 deque([]) 0 0
nx, ny 인덱스의 값 -1 0
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 0
노드가 1인 인덱스 1 0
nx, ny 인덱스의 값 0 -1
조건문 continue로 다음 루프
nx, ny 인덱스의 값 0 1
조건문 continue로 다음 루프
시작 큐 deque([]) 1 0
nx, ny 인덱스의 값 0 0
조건문 continue로 다음 루프
nx, ny 인덱스의 값 2 0
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 -1
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 1
노드가 1인 인덱스 1 1
시작 큐 deque([]) 1 1
nx, ny 인덱스의 값 0 1
조건문 continue로 다음 루프
nx, ny 인덱스의 값 2 1
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 0
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 2
노드가 1인 인덱스 1 2
시작 큐 deque([]) 1 2
nx, ny 인덱스의 값 0 2
노드가 1인 인덱스 0 2
nx, ny 인덱스의 값 2 2
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 1
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 3
노드가 1인 인덱스 1 3
시작 큐 deque([(1, 3)]) 0 2
nx, ny 인덱스의 값 -1 2
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 2
조건문 continue로 다음 루프
nx, ny 인덱스의 값 0 1
조건문 continue로 다음 루프
nx, ny 인덱스의 값 0 3
조건문 continue로 다음 루프
시작 큐 deque([]) 1 3
nx, ny 인덱스의 값 0 3
조건문 continue로 다음 루프
nx, ny 인덱스의 값 2 3
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 2
조건문 continue로 다음 루프
nx, ny 인덱스의 값 1 4
노드가 1인 인덱스 1 4
....
시작 큐 deque([]) 4 0
nx, ny 인덱스의 값 3 0
조건문 continue로 다음 루프
nx, ny 인덱스의 값 5 0
조건문 continue로 다음 루프
nx, ny 인덱스의 값 4 -1
조건문 continue로 다음 루프
nx, ny 인덱스의 값 4 1
조건문 continue로 다음 루프
"""
초기 그래프의 모습
[
[1, 0, 1, 0, 1, 0],
[1, 1, 1, 1, 1, 1],
[0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1]
]
방문한곳을 증가시키며 반복한 최종 그래프의 모습
[
[1, 0, 5, 0, 7, 0],
[2, 3, 4, 5, 6, 7],
[0, 0, 0, 0, 0, 8],
[14, 13, 12, 11, 10, 9],
[15, 14, 13, 12, 11, 10]
]