시간 복잡도

처음 시간 복잡도를 접했을때는 시간이 얼마나 걸리는지 표현하거구나~ 로 넘어갔다.
그렇게 넘어가고 최근 알고리즘 강의를 듣다 보니 시간 복잡도를 알아야 어떤 알고리즘으로 문제를 해결해야 할지 결정할 수 있겠다 싶어 시간 복잡도에 대해 찾아보았다.

알고리즘에서 시간 복잡도는 주어진 문제를 해결하기 위한 연산 횟수를 말한다.
내가 현재 알고리즘 해결을 위해 사용할수 있는 언어가 파이썬 이기 때문에 파이썬 기준으로 2,000만 번~1억 번의 연산을 1초의 수행 시간으로 예측할 수 있다.

빅-오(Xn)

알고리즘의 시간 복잡도를 나타낼때 많이 사용하는 빅오 표기법이다. 조건이 최악으로 주어져 계산횟수의 경우에서 가장 많은 계산을 할때를 나타낸 표기법이다. 실제 테스트에서는 1개의 테스트 케이스로 합,불을 결정하지 않기 때문에 최악의 조건을 생각해야 한다.

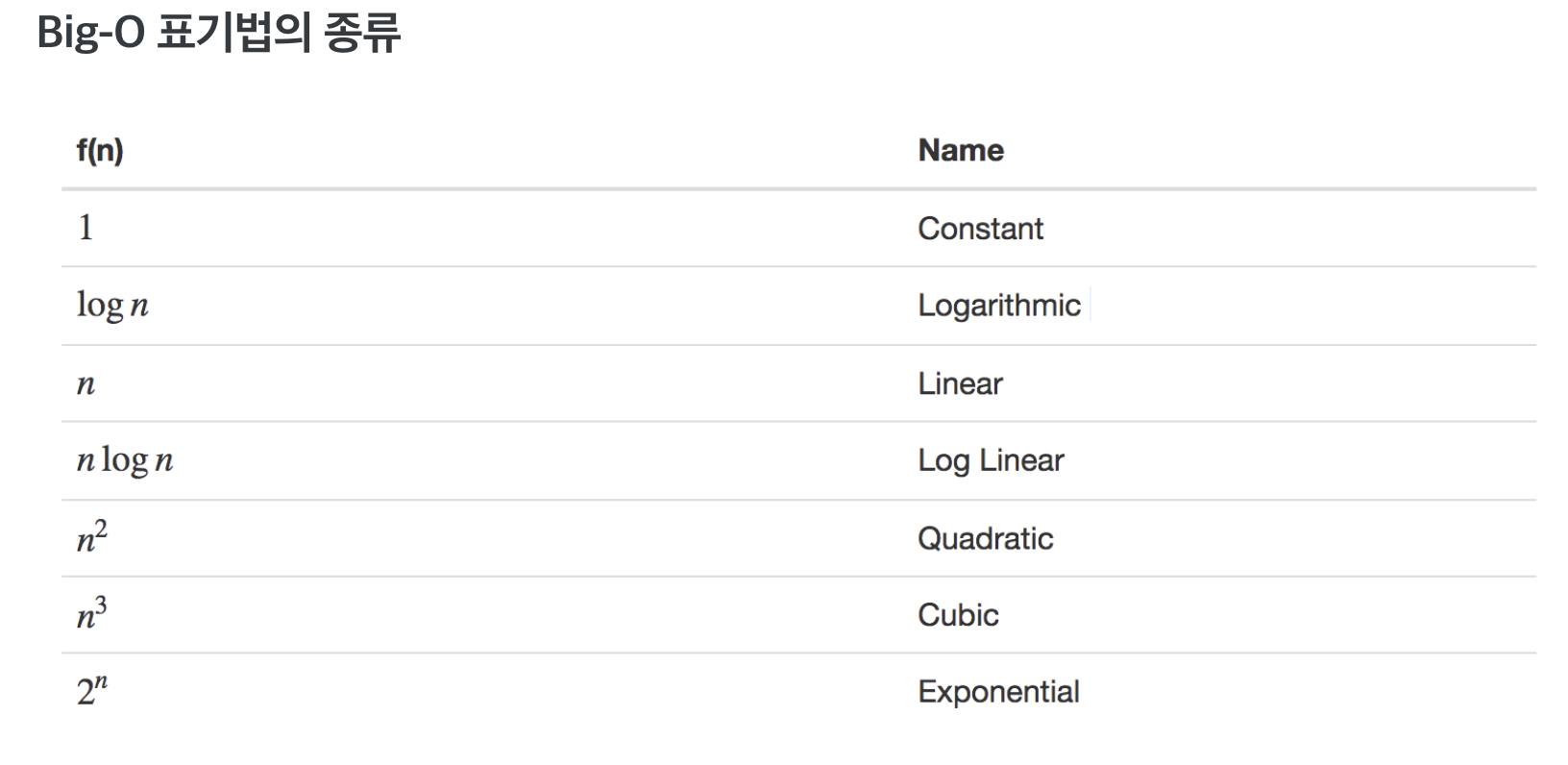
• O(1) - (상수) Constant
  입력되는 데이터양과 상관없이 일정한 실행 시간을 가진다.
  알고리즘이 문제를 해결하는데 오직 한 단계만 거친다.

• O(logN) Logarithmic
  데이터양이 많아져도, 시간이 조금씩 늘어난다.
  시간에 비례하여, 탐색 가능한 데이터양이 2의 n승이 된다.
  문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다.
  만약 입력 자료의 수에 따라 실행 시간이 이 log N 의 관계를 만족한다면 N이 증가함에 따라 실행시간이 조금씩 늘어난다. 이 유형은 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤때 나타나는 유형이다.
  Binary Search

• O(N) Linear
  데이터양에 따라 시간이 정비례한다.
  linear search, for 문을 통한 탐색을 생각하면 되겠다.

• O(N log N) log linear
  데이터양이 N배 많이 진다면, 실행 시간은 N배 보다 조금더 많아 진다. (정비례 하지 않는다.)
  이 유형은 커다란 문제를 독립적인 작은 문제로 쪼개어 각각에 대해 독립적으로 해결하고,나중에 다시 그것들을 하나로 모으는 경우에 나타난다. N이 두배로 늘어나면 실행 시간은 2배보다 약간 더 많이 늘어난다.
  퀵소트, 머지소트

• O(N^2) Quadratic
  데이터양에 따라 걸리는 시간은 제곱에 비례한다. (효율이 좋지 않음, 사용하면 안된다)
  이 유형은 이중루프내에서 입력 자료를 처리 하는 경우에 나타난다. N값이 큰값이 되면 실행 시간은 감당하지 못할 정도로 커지게 된다.
  문제를 해결하기 위한 단계의 수는 입력값 n의 제곱
  2중 for 문을 사용하는 버블소트, 삽입정렬(insertion sort)

https://wayhome25.github.io/cs/2017/04/20/cs-26-bigO/

적절한 알고리즘 선택하기

백준 홈페이지에서 문제 하나를 예로들면, 아래 문제의 N의 범위는 1,000,000(백만)시간제한은 1초로 되어있다. 즉 2000만번 이하의 연산으로 답을 구해야한다. 연산 횟수는 알고리즘 시간 복잡도 n의 값에 데이터의 최대 크기를 대입하여 도출 할 수있다.

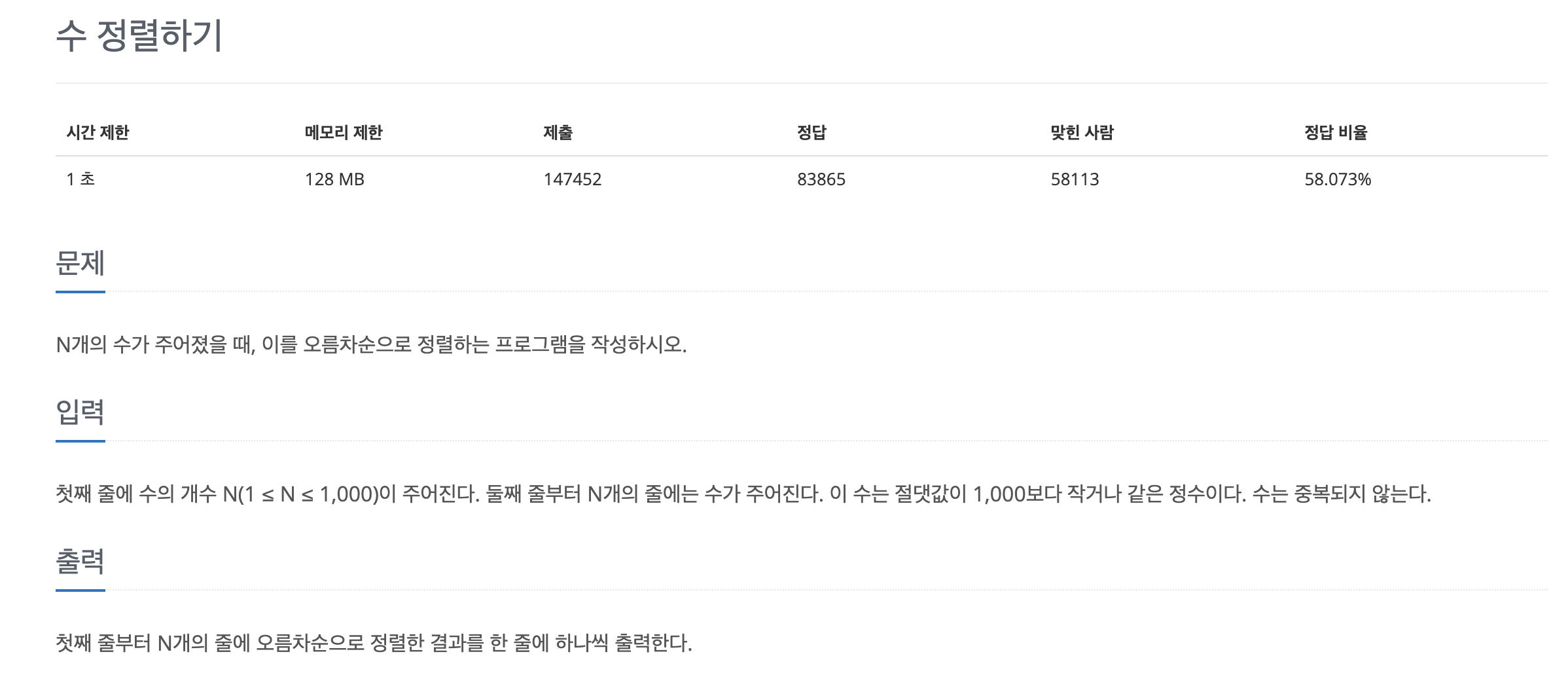
선택 또는 삽입 정렬의 시간 복잡도는 O(N**2)로 백만 X 백만이 된다.
1,000,000 x 1,000,000 = 1,000,000,000,000 너무 큰 숫자이다 1초안에 못할거라는 결론이 나오고 다른 알고리즘을 사용해야 하는데 계수 정렬또는 퀵정렬을 사용해보자. 계수정렬은 O(K+N), 퀵정렬은 O(logN)이기 때문에 두가지중 하나를 사용할 것이고 이후에 버블 정렬을 공부하고 버블 정렬로도 추가하겠다.
처음에 계수정렬으로 제출했는데 계속 오답처리가 되었다. vscode에서 출력이 잘 나와 뭐가 문제인지 한참 찾았는데 문제의 조건에 절댓값이 1000보다 작거나 같은 정수라고 되어있는것을 못봤다...
계수정렬의 경우 음수면 배열의 크기를 적절히 늘려 주어야 하기 때문에 지금 내가 아는 정렬 방법중 가장 빠른 퀵정렬으로 작성해 보았다.

퀵정렬은 재귀를 사용한 코드이기 때문에 재귀의 깊이를 지정하는 함수를 사용해줘야한다.

import sys
sys.setrecursionlimit(원하는 재귀 깊이)

파이썬의 기본 재귀 깊이 제한은 1000이다.

import sys
sys.setrecursionlimit(99999)

def quickSort(array, start, end):
    if (start >= end):
        return
    pivot = start
    left = start + 1
    right = end
    while (left <= right):
        while (left <= end and array[left] <= array[pivot]):
            left += 1
        while (right > start and array[right] >= array[pivot]):
            right -= 1
        if (left > right):
            array[right], array[pivot] = array[pivot], array[right]
        else:
            array[left], array[right] = array[right], array[left]
    quickSort(array, start, right-1)
    quickSort(array, right+1, end)

N = int(sys.stdin.readline())

array = []
for i in range(N):
    array.append(int(sys.stdin.readline()))

quickSort(array, 0, len(array)-1)

for i in array: print(i)

사실 이걸 이렇게 길게 정리하려고 한건 아닌데 문제가 간단해 짧게 정리될줄 알았다ㅎㅎㅎ
아무튼 중요한건 문제에 나온 조건을 잘 살펴보고 적절한 알고리즘을 선택해야한다.

시간 복잡도 계산

코드의 모든 연산 횟수를 더하고 그중 가장 차수가 높은 n만 표기하는게 빅오 표기법이다.

알고리즘 분석에 인정되는 연산

• 변수에 값을 배정
• 함수를 호출
• 산술연산(더하기, 빼기, 곱하기, 나누기 등)
• 비교연산(크다, 작다, 같다, 아니다)
• 인덱싱을 이용한 코드
• 반환(return)
• 참조 또는 내부 속성 접근

아래 코드의 연산 횟수를 더해 시간 복잡도를 구하면 아래와 같다.

a=5 # Constant 1
b=6 # Constant 1
c=10 # Constant 1
for i in range(n):
 for j in range(n):
    x = i * i # n^2 => for문 중첩 사용
    y = j * j # n^2
    z = i * j # n^2
for k in range(n):
 w = a*k + 45 # n
 v = b*b # n
d = 33 # Constant 1

T(n) = 3 + 3ㅜㅜn^2 + 2n + 1 = 3n^2 + 2n + 4 = O(n^2)