[코테]24-BFS1

BFS

• BFS의 목적은 임의의 정점에서 시작해서, 모든 정점을 한 번씩 방문하는 것.
• BFS는 최단 거리를 구하는 알고리즘.
• BFS는 모든 가중치가 1일 때, 최단 거리를 구하는 알고리즘임.
• 모든 가중치가 1이 아닐 때는 Dijkstra임

*BFS를 이용해 해결할 수 있는 문제는 아래와 같은 조건을 만족해야 한다.
1. 최소 비용 문제이어야 한다
2. 간선의 가중치가 1이어야 한다.
3. 정점과 간선의 개수가 적어야한다. ( 적다는 것은 문제의 조건에 맞춰서 해결할 수 있다는 것을 의미한다.)

• 간선의 가중치가 문제에서 구하라고 하는 최소 비용과 의미가 일치해야한다.
  즉, 거리의 최소값을 구하는 문제라면 가중치 = 거리 , 시간의 최소값을 구하는 문제라면 가중치는 시간을 의미해야한다.

숨바꼭질(1697)

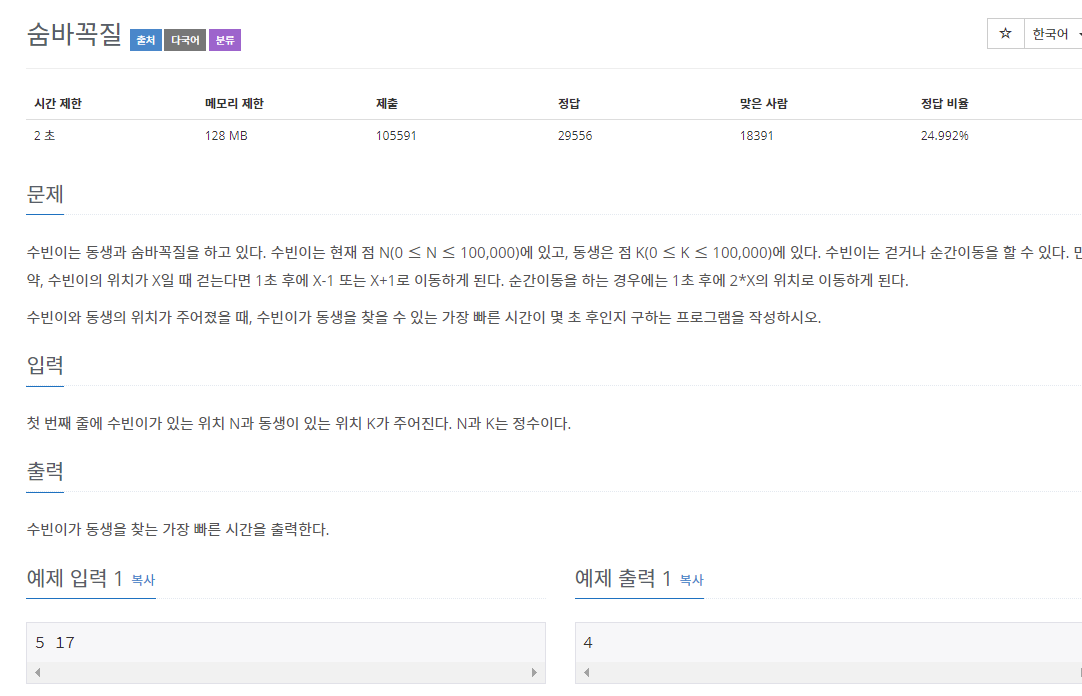
수빈이의 위치 : N
동생의 위치 : K
동생을 찾는 가장 빠른 시간을 구하는 문제.

• 수빈이가 할 수 있는 행동 (위치:X)

1. 걷기 : X+1 또는 X-1로 이동(1초)
2. 순간이동: 2*X로 이동(1초)

• 위치 -> 위치

• 여기서 위치가 정점, -> 는 간선으로 표현할 수 있음.

• 문제의 제한은 1<=N,K<=10만
• 정점은 최대 M개(10만), 간선은 3M개.

• O(V+E) => 4M 이기 때문에 40만정도 나오니까 BFS 가능함.
• 절대 20만을 넘을 수 없음. 따라서 MAX 20만으로 잡아주는 것이 좋음.

check[i] = i를 방문했는지 -> F/T
dist[i] = i를 몇 번만에 방문했는지.

ex) now -> next를 갔다고 가정한다면
가능한 next는 2*now / now+1 / now-1 세가지가 있음.

• 시작점 넣어주어야 함.
  check[n]= true;
  dist[n]=1;

import java.util.*;

class Main {
	static final int MAX = 200000;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int k = sc.nextInt();
		boolean chk[] = new boolean[MAX];
		int d[] = new int[MAX];
		
		// 초기값 선언
		chk[n]=true;
		d[n]=0;
		Queue<Integer> q = new LinkedList<Integer>();
		q.add(n);
		
		while(!q.isEmpty()) {	//queue가 비어있지 않을때까지
			int now = q.remove();
			if(now-1 >= 0) {
				if(chk[now-1] == false) {
					q.add(now-1);
					chk[now-1] = true;
					d[now-1] = d[now]+1;
				}
			}
			if(now+1 < MAX) {
				if(chk[now+1] == false) {
					q.add(now+1);
					chk[now+1] = true;
					d[now+1] = d[now]+1;
				}
			}
			if(now*2 < MAX) {
				if(chk[now*2] == false) {
					q.add(now*2);
					chk[now*2] = true;
					d[now*2] = d[now]+1;
				}
			}
		}
		System.out.println(d[k]);
	}
}

숨바꼭질 4(13913)

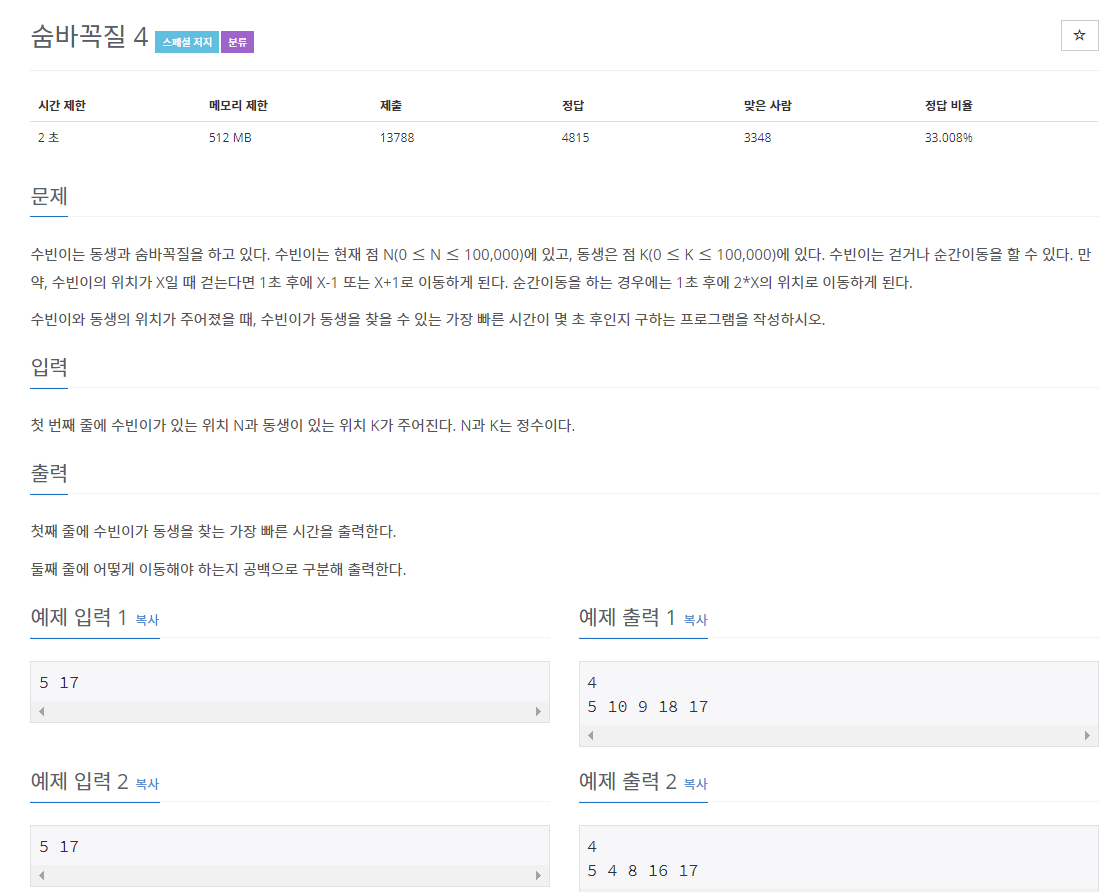
숨바꼭질 1과 똑같은 문제이지만 가장 빠른 시간 + 이동하는 방법까지 구하는 문제임.

• 다이나믹 LIS, 역추적 -> 대부분의 역추적은 비슷함.
  LIS의 점화식은 D[i]= max(D[j])+1 (j<i , A[j]<A[i])

• 어떤 값이 다른 값에 의해서 변경되기 때문임.

• from[i] : i가 어디에서 온건지를 배열에 넣어주는 것. 그래서 역추적가능함.
• n -> k 를 가는 방법을 찾는 문제임.
  => 따라서 k부터 시작을 해야함. 왜냐면 역추적해야하기 때문.
  k는 from[k]에서 왔음. 그리고 from[k]는 from[k2]
  ....
  from[k2] -> from[k] -> k
  이런식이기 때문에 뒤에서부터 역추적해주면 됨.

1) 재귀함수 사용
void print(int n, int m){ //n->m으로 가는 방법.
...

}
n -> ... -> from[m] ->m 을 가는 것. 이것을 print(n,m)으로 표현이 가능하다.

1. 재귀함수를 이용한 구현

import java.util.*;

class Main {
	static final int MAX = 200000;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int k = sc.nextInt();
		boolean chk[] = new boolean[MAX];
		int d[] = new int[MAX];
		int from[] = new int[MAX];
		
		// 초기값 선언
		chk[n]=true;
		d[n]=0;
		Queue<Integer> q = new LinkedList<Integer>();
		q.add(n);
		
		while(!q.isEmpty()) {
			int now = q.remove();
			if(now-1 >= 0) {
				if(chk[now-1] == false) {
					q.add(now-1);
					chk[now-1] = true;
					d[now-1] = d[now]+1;
					from[now-1]=now;
				}
			}
			if(now+1 < MAX) {
				if(chk[now+1] == false) {
					q.add(now+1);
					chk[now+1] = true;
					d[now+1] = d[now]+1;
					from[now+1]=now;
				}
			}
			if(now*2 < MAX) {
				if(chk[now*2] == false) {
					q.add(now*2);
					chk[now*2] = true;
					d[now*2] = d[now]+1;
					from[now*2]=now;
				}
			}
		}
		System.out.println(d[k]);
		print(from, n, k);
		System.out.println();
	}
	
	static void print(int from[],int n,int k) {
		if(n!=k) {
			print(from,n,from[k]);
		}
		System.out.println(k+" ");
		
	}
}

2. stack으로 구현

import java.util.*;

class Main {
	static final int MAX = 200000;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int k = sc.nextInt();
		boolean chk[] = new boolean[MAX];
		int d[] = new int[MAX];
		int from[] = new int[MAX];
		
		// 초기값 선언
		chk[n]=true;
		d[n]=0;
		Queue<Integer> q = new LinkedList<Integer>();
		q.add(n);
		
		while(!q.isEmpty()) {
			int now = q.remove();
			if(now-1 >= 0) {
				if(chk[now-1] == false) {
					q.add(now-1);
					chk[now-1] = true;
					d[now-1] = d[now]+1;
					from[now-1] = now;
				}
			}
			if(now+1 < MAX) {
				if(chk[now+1] == false) {
					q.add(now+1);
					chk[now+1] = true;
					d[now+1] = d[now]+1;
					from[now+1] = now;
				}
			}
			if(now*2 < MAX) {
				if(chk[now*2] == false) {
					q.add(now*2);
					chk[now*2] = true;
					d[now*2] = d[now]+1;
					from[now*2] = now;
				}
			}
		}
		System.out.println(d[k]);
		print(from, n, k);
		System.out.println();
	}
	
	static void print(int from[],int n,int k) {
		Stack<Integer> stack = new Stack<Integer>();
		for(int i=k;i!=n; i=from[i]) {
			stack.push(i);
		}
		stack.push(n);
		while(!stack.isEmpty()) {
			System.out.println(stack.pop()+" ");
		}
		
	}
}

=> 이렇게 stack쓰는 연습을 좀 해야해야겠다.. 오늘 코테에 stack이 나왔기 때문임;;ㅎㅎ

최백준 선생님의 코딩테스트 기초 강의를 보고 작성한 글입니다.