[코테]23-그래프의 탐색

그래프의 탐색

목적 : 한 정점에서 시작해서 연결된 모든 정점을 한 번씩 방문하는 것.
DFS : 깊이 우선 탐색
-> 사람 1명(시작점) -> 돌아가야 할 스택
BFS : 너비 우선 탐색
-> 사람1명 -> 사람을 복제해서 ,,,

깊이 우선 탐색(DFS)

Depth First Search
스택을 이용해서 갈 수 있는 만큼 최대한 많이 가고, 갈 수 없으면 이전 정점으로 돌아간다.

• 정점을 방문했는지 방문하지 않았는지를 체크하는 배열이 필요함.
• check[i] : i를 방문했으면 1, 아니면 0
• 갈 수 있는 곳이 여러개 있을 때 어디로 가는지는 중요하지 않음.
• 다 돌아가서 갈 곳이 없으면 스택을 이용해서 원래의 정점으로 돌아감.
• 실제로는 스택 이용하지 않고, 재귀 함수를 이용

재귀 호출을 이용해서 구현.

인접행렬을 이용한 구현

DFS(X) -> X를 방문했다는 것.

void dfs(int x){
check[x] = true; //방문했다는 뜻.
for(int i=1; i<=n; i++){
if(a[x][i] == 1 && check[i] == false){
dfs(i); } } }

조건문 내용 x-> i
1) x와 i사이에 간선이 있음.
2) i를 방문한 적이 없음

• 각 정점마다 dfs 1번 호출. -> V번 (정점의 개수)

• DFS함수의 복잡도 : V.

• 시간복잡도 : O(V^2)

  인접리스트로 구할 때

  void dfs(int x){
  check[x]= true;
  for(int i=0;i<a[x].size(); i++){
  int y=a[x][i];
  if(check[y] ==false){
  dfs(y);
  }}}

  1) x->i
  a[x] = x와 연결된 모든 정점.
  -> check[y] =false인 것만 확인해주면 된다.

• dfs(1) : 1과 연결된 간선의 개수와 같음.
  -> 1과 연결된 모든 간선에 대해서 for문을 돌려서 검사를 하는 것.
  -> 이런식으로 전부 다 계산하면 모든 정점에 대해서 검사를 하게 됨.

• 시간복잡도 : O(E)

  너비 우선탐색(BFS)

  Breadth First Search
  큐를 이용해서 지금 위치에서 갈 수 있는 것을 모두 큐에 넣는 방식.
  큐에 넣을 때 방문했다고 체크해야한다.

• dfs에서 방문 = 함수의 호출.
  but, BFS에서의 방문 = 큐에 넣을 때.
• 이미 방문한 것을 또 방문하면 안됨!
• 그렇기 때문에 큐에 넣을 때 방문했다고 해야함.
• 큐가 비어있게 되면 탐색이 끝난 것임.

BFS의 구현은 큐를 이용해서 할 수 있음.(인접행렬)

• 목적 : 모든 정점을 한 1번씩 방문. 큐에 push. pop이 됨.
• 시간복잡도 : O(V^2)

**BFS 인접리스트를 사용하면 O(V+E)

DFS와 BFS(1260)

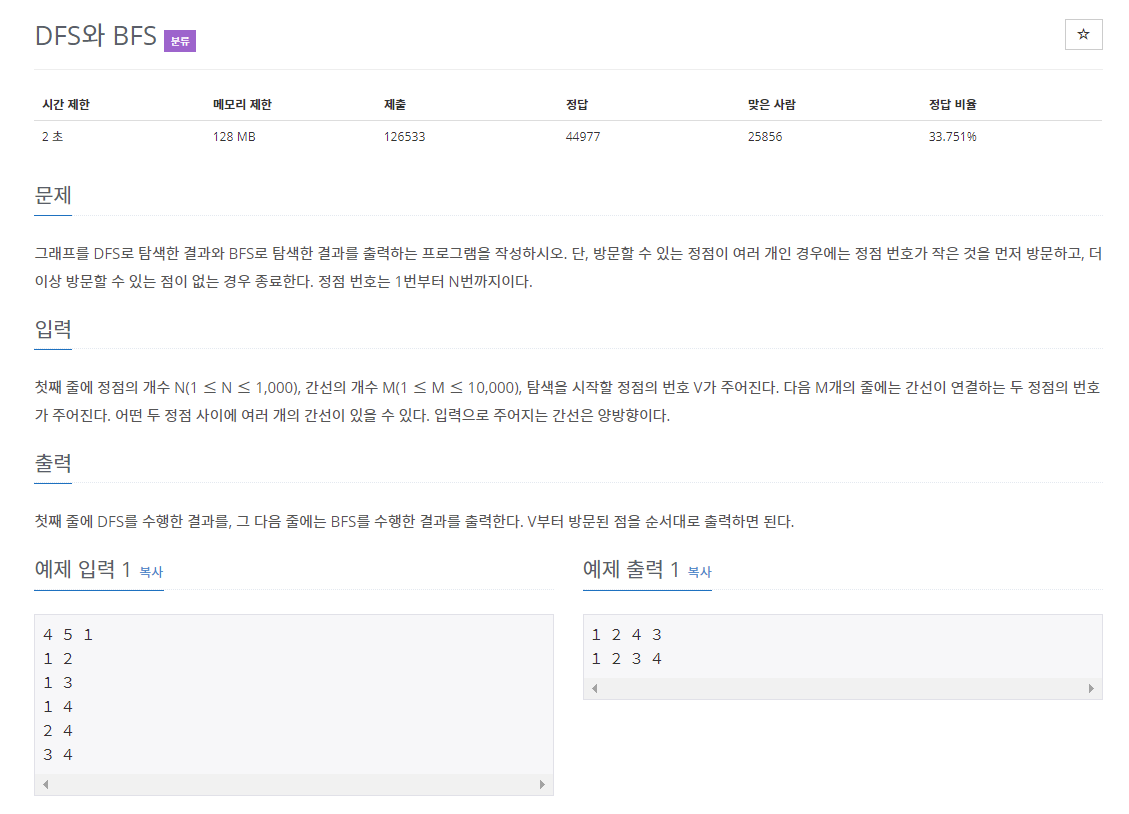
• 정렬해주어야 함.

import java.util.*;


class Main {
	static ArrayList<Integer> arr[];
	static boolean chk[];
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();
		int begin = sc.nextInt();
		arr = new ArrayList[n+1];
		
		for(int i=1;i<=n;i++) {
			arr[i] = new ArrayList<Integer>();
		}
		for(int i=0;i<m;i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
			arr[u].add(v);
			arr[v].add(u);
		}
        //여기까지는 입력받고
        
		for(int i=1;i<=n;i++) {
			Collections.sort(arr[i]); //정렬
		}
		chk = new boolean[n+1];
		dfs(begin);
		System.out.println();
		chk = new boolean[n+1];
		bfs(begin);
		System.out.println();
	}
	
    //dfs 함수. 재귀함수 이용해서 계속 호출하고 true(방문함)
	public static void dfs(int x) {
		if(chk[x]) {
			return;
		}
		chk[x]=true;
		System.out.print(x+" ");
		for(int y : arr[x]) {
			if(chk[y]==false) {
				dfs(y);
			}
		}
	}
    //bfs 함수. queue 이용
	public static void bfs(int x) {
		Queue<Integer> q = new LinkedList<Integer>();
		q.add(x);
		chk[x] = true;
		while(!q.isEmpty()) {
			int a = q.remove();
			System.out.print(a+" ");
			for(int y : arr[a]) {
				if(chk[y]==false) {
					chk[y]=true;
					q.add(y);
				}
			}
		}
		
	}
}

연결요소(11724)

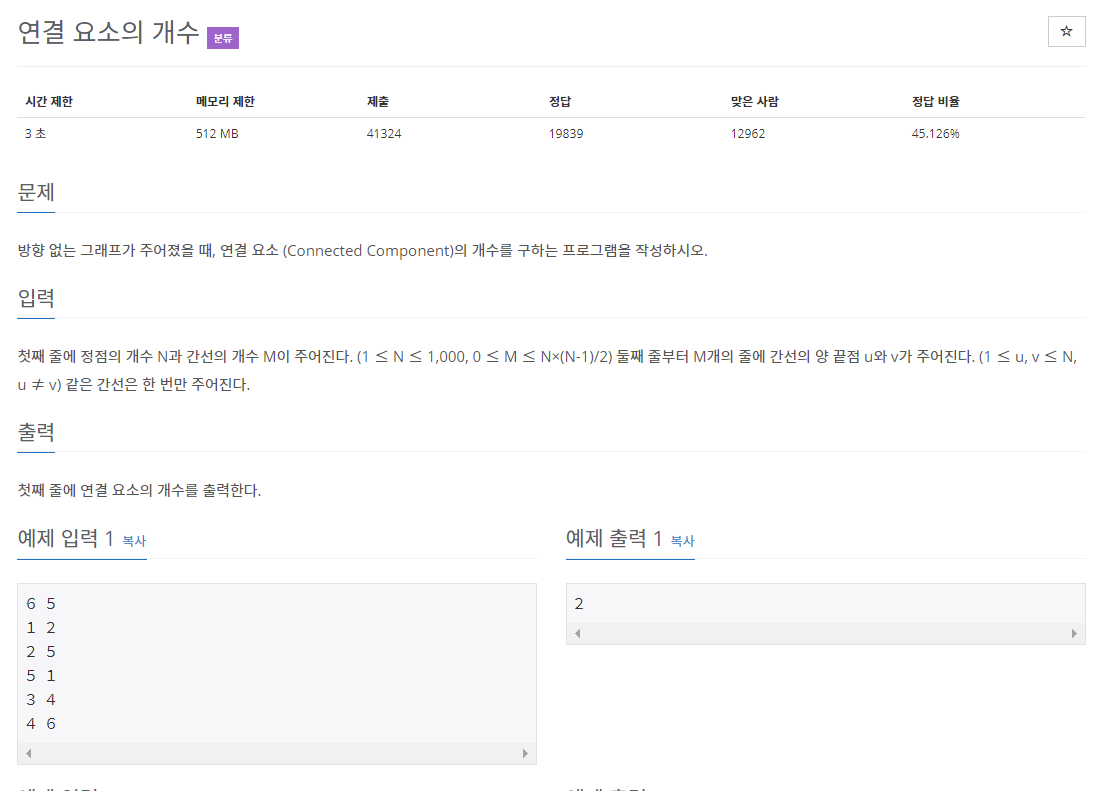
그래프가 나누어져 있지 않은 경우가 있을 수 있다.
나누어진 각각의 그래프를 연결 요소라고 한다.
연결 요소에 속한 모든 정점을 연결하는 경로가 있어야 한다.
또, 다른 연결 요소에 속한 정점과 연결하는 경로가 있으면 안된다.

• 연결 요소를 구하는 것은 DFS나 BFS 탐색을 이용해서 구할 수 있음.

import java.util.*;


class Main {
	static ArrayList<Integer> arr[];
	static boolean chk[];
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int m = sc.nextInt();
		arr = new ArrayList[n+1];
		
		for(int i=1;i<=n;i++) {
			arr[i] = new ArrayList<Integer>();
		}
		for(int i=0;i<m;i++) {
			int u = sc.nextInt();
			int v = sc.nextInt();
			arr[u].add(v);
			arr[v].add(u);
		}
		boolean c[] = new boolean[n+1];
		int res=0;
		for(int i=1;i<=n;i++) {
			if(c[i]==false) {
				dfs(arr,c,i);
				res ++;
			}
		}
		System.out.println(res);
	}
	
	public static void dfs(ArrayList<Integer> arr[], boolean chk[], int x) {
		if(chk[x]) {
			return;
		}
		chk[x]=true;
		for(int y : arr[x]) {
			if(chk[y]==false) {
				dfs(arr,chk,y);
			}
		}
	}
}

-> 위에 코드에서 살짝만 변형했다,,

이분 그래프(1707)

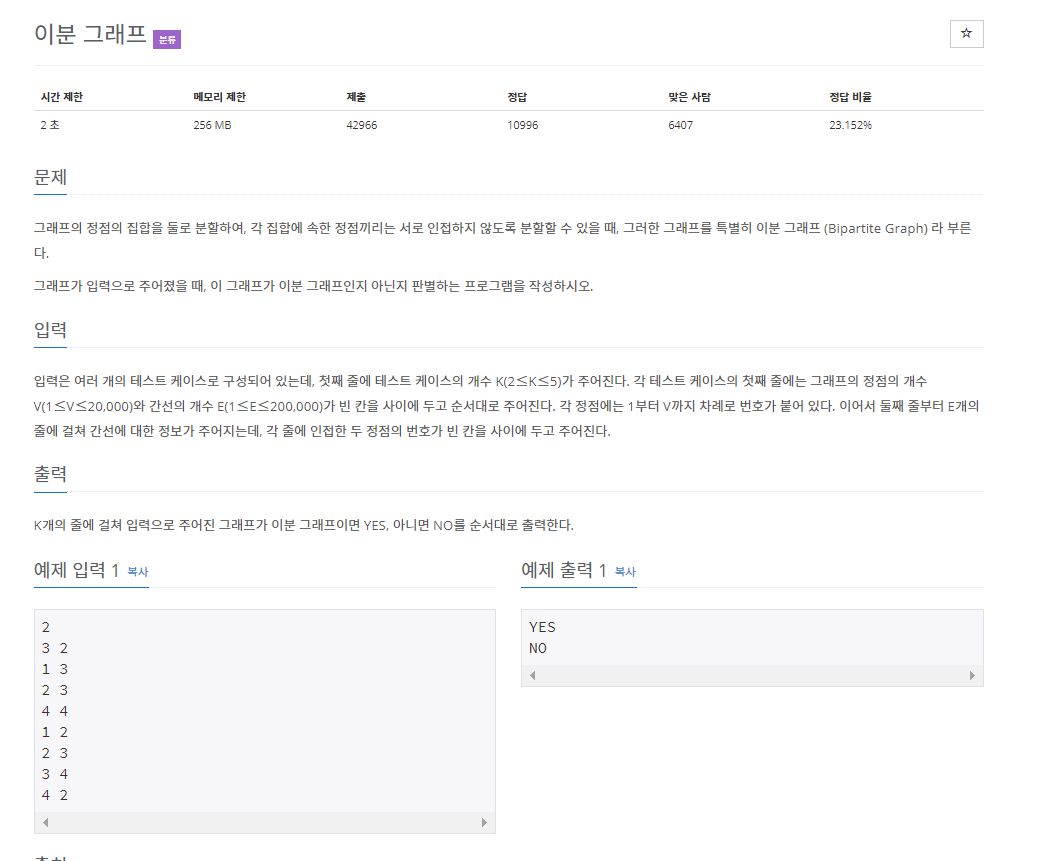
그래프를 A와 B로 나눌 수 있으면 이분 그래프라고 한다.
A에 포함된 정점끼리 연결된 간선이 없음.
B에 포함된 정점끼리 연결된 간선이 없음.
모든 간선의 한 끝 점은 A에, 다른 끝 점은 B에 있어야 함.

• DFS / BFS 탐색으로 이분 그래프인지 아닌지 알아낼 수 있다.

import java.util.*;


class Main {
	static ArrayList<Integer> arr[];
	static boolean chk[];
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int t = sc.nextInt();
		while(t-->0) {
			int n = sc.nextInt();
			int m = sc.nextInt();
			arr = new ArrayList[n+1];
			for(int i=1;i<=n;i++) {
				arr[i] = new ArrayList<Integer>();
			}
			for(int i=0;i<m;i++) {
				int u = sc.nextInt();
				int v = sc.nextInt();
				arr[u].add(v);
				arr[v].add(u);
			}
			int color[] = new int[n+1];
			boolean c = true;
			for(int i=1;i<=n;i++) {
				if(color[i]==0) {
					if(dfs(arr, color,i,1)==false) {
						c=false;
					}
				}
			}
			if(c) {
				System.out.println("YES");
			}else {
				System.out.println("NO");
			}
		}
	}
	
	public static boolean dfs(ArrayList<Integer> arr[], int color[], int x,int c) {
		color[x]=c;
		for(int y : arr[x]) {
			if(color[y]==0) {
				if(dfs(arr,color,y,3-c)==false) {
					return false;
				}
			}else if(color[y]==color[x]) {
				return false;
			}
		}
		return true;
	}
}

단지번호붙이기(2667)

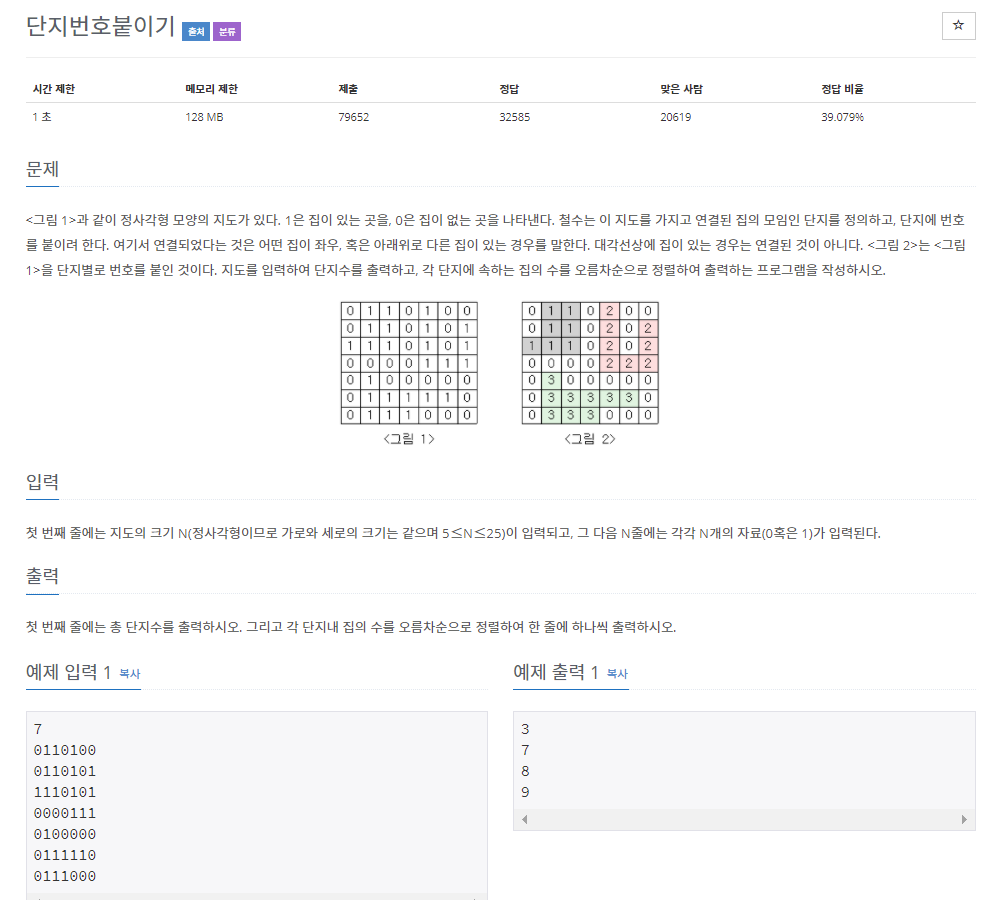
정사각형 모양의 지도가 있다.
0은 집이 없는 곳, 1은 집이 있는 곳.
지도를 가지고 연결된 집의 모인인 단지를 정의하고 단지에 번호를 붙인다.
연결 : 좌우 아래 위로 집이 있는 경우.

• 단지 : 연결요소의 개수.
• 단지내의 개수 : 정점의 개수.

• 그래프 문제를 풀 때 인접리스트를 만듬 -> 한 정점과 연결된 다른 정점 (간선) 효율적으로 찾기 위해서.

• DFS나 BFS 알고리즘을 이용해서 어떻게 이어졌는지 확인할 수 있다.
  d[i][j] = (i,j)를 방문안했으면 0, 아니면 1

• bfs는 방법이 정해져 있음. 시작점 넣고, 큐가 비어있지 않으면 다음거 넣고 ~ 이런식으로. 그래서 비슷한 형태의 코드를 가짐.

• dx = [1,-1,0,0]

• dy = [ 0,0,1,-1]
  상하좌우만 들어있으면 됨.

import java.util.*;

class Pair{
	int x;
	int y;
	Pair(int x, int y){
		this.x = x;
		this.y = y;
	}
}
class Main {
	static final int dx[]= {0,0,1,-1};
	static final int dy[]= {1,-1,0,0};
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		int cnt=0;
		int d[][] = new int[n][n];
		
		sc.nextLine();
		int arr[][] = new int [n][n];
		for(int i=0;i<n;i++) {
			String str = sc.nextLine();
			for(int j=0;j<n;j++) {
				arr[i][j] = str.charAt(j)-'0';
			}
		}
		for(int i=0;i<n;i++) {
			for(int j=0;j<n;j++) {
				if(arr[i][j] == 1 && d[i][j]==0) {
					dfs(arr, d, i, j, ++cnt, n);
				}
			}
		}
		int res[] = new int[cnt];
		for(int i=0;i<n;i++) {
			for(int j=0;j<n;j++) {
				if(d[i][j] != 0)
					res[d[i][j]-1]++;
			}
		}
		Arrays.sort(res);
		System.out.println(cnt);
		for(int i=0;i<cnt;i++) {
			System.out.println(res[i]);
		}
	}
	
	public static void dfs(int arr[][],int d[][],int x,int y, int cnt, int n) {
		d[x][y]= cnt;
		for(int k=0; k<4; k++) {
			int nx= x+dx[k];
			int ny= y+dy[k];
			if(0<=nx && nx <n && 0 <=ny && ny < n) {
				if(arr[nx][ny] == 1 && d[nx][ny] == 0) {
					dfs(arr, d, nx, ny, cnt, n);
				}
			}
		}
	
	}
}

=> 이런식의 문제를 많이 푸는 연습을 해야할 것 같음...ㅠ-ㅠ

미로 검색(2178)

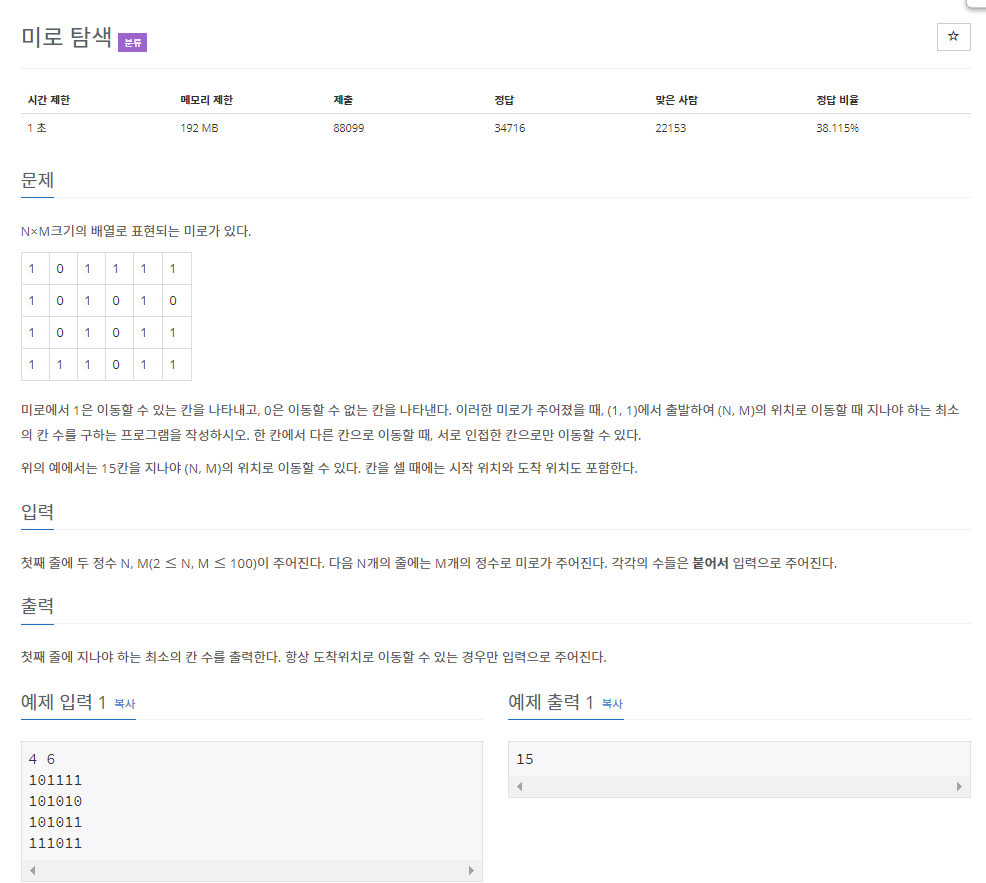
(1,1)에서 (N,M)으로 가는 가장 빠른 길을 구하는 문제
DFS 탐색으로는 풀 수 없다.
BFS 탐색을 사용해야 한다.
BFS는 단계별로 진행된다는 사실을 이용

• 최단 경로 => BFS 탐색.
• 가중치가 1일 때만 최단 경로를 구할 수 있음.

• 방문여부만 검색하는 것이 아니라, 거리를 넣어줘야해서 이차원배열로 풀어야함.
• dist[][];
• chk[][] , dist[][] 두 개의 배열 사용.