[Algorithm] 2-5 Merge Sort(병합 정렬)

정렬 알고리즘
1. Bubble Sort(거품 정렬)
2. Selection Sort(선택 정렬)
3. Insertion Sort(삽입 정렬)
4. Quick Sort(퀵 정렬)
5. Merge Sort(병합 정렬) ⇠
6. Heap Sort(힙 정렬)
7. Radix Sort(기수 정렬)
8. Counting Sort(계수 정렬)

기본 개념

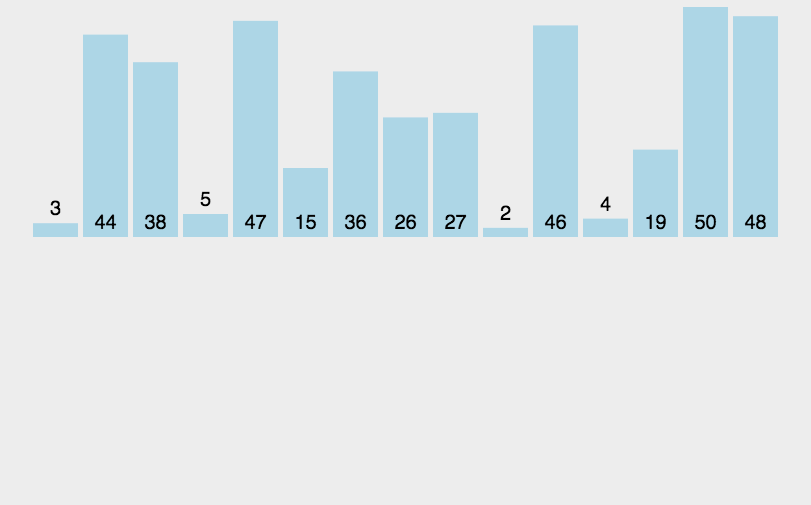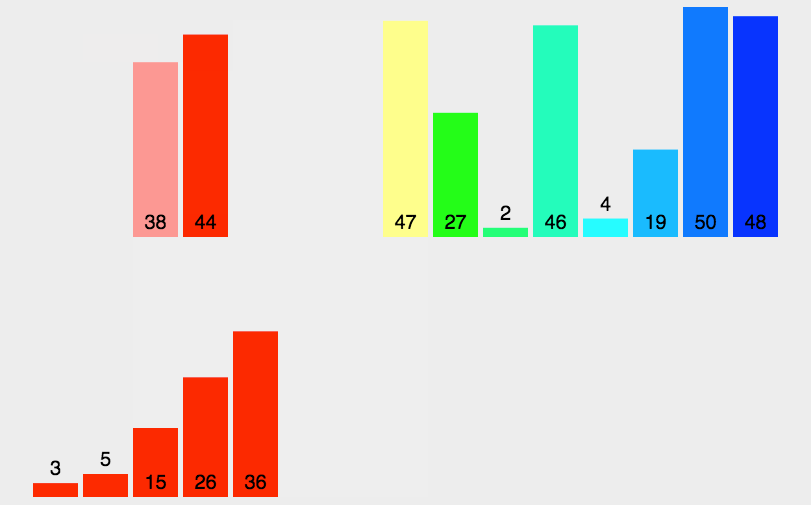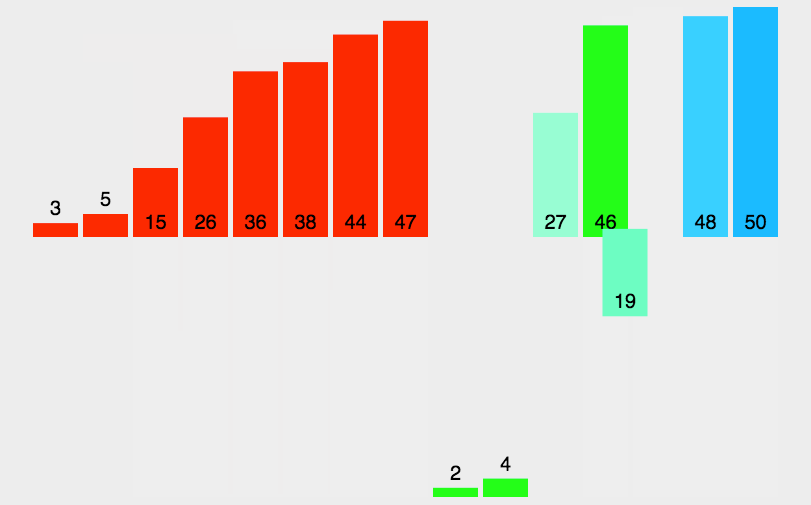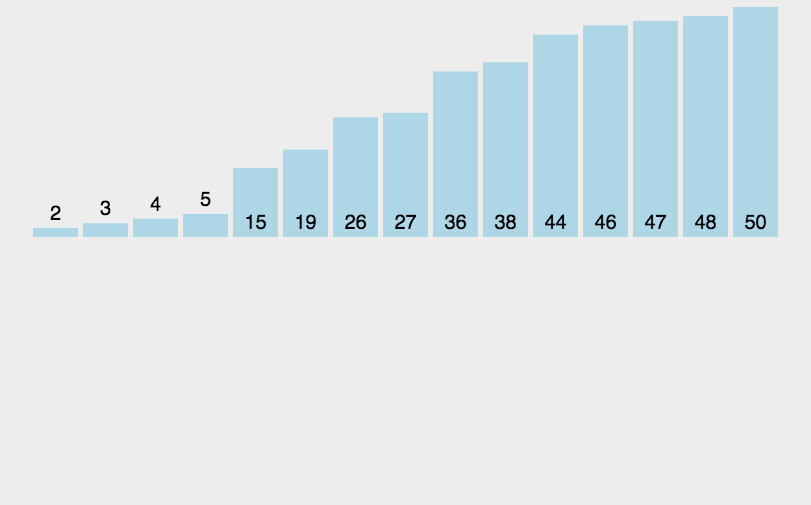
• 분할 정복(Divide and Conquer) 기법과 재귀 알고리즘을 이용한 정렬 알고리즘
• 주어진 배열을 원소가 하나 밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기순으로 재배열하면서 원래 크기의 배열로 합친다.
• 퀵 정렬과는 반대로 안정 정렬이다.

퀵 정렬과의 차이점

퀵 정렬 : 우선 피벗을 통해 정렬(partition) → 영역을 쪼갬(Quick Sort)
병합 정렬 : 영역을 쪼갤 수 있을 만큼 쪼갬(Merge Sort) → 정렬(Merge)

특징

• 알고리즘을 큰 그림에서 보면 분할(split) 단계와 병합(merge) 단계로 나눌 수 있으며, 단순히 중간 인덱스를 찾아야 하는 분할 비용보다 모든 값들을 비교해야하는 병합 비용이 크다.
• 다른 정렬 알고리즘과 달리 인접한 값들 간에 상호 자리 교대(swap)이 일어나지 않는다.

구현(Java)

과정

1. 리스트의 길이가 0 또는 1이면 이미 정렬된 것으로 본다. 그렇지 않은 경우에는
2. 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
3. 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
4. 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.

2개의 정렬된 리스트를 합병(merge)하는 과정
① 2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트(sorted)로 옮긴다.
② 둘 중에서 하나가 끝날 때까지 이 과정을 되풀이한다.
③ 만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트(sorted)로 복사한다.
④ 새로운 리스트(sorted)를 원래의 리스트(list)로 옮긴다.

최적화

병합 결과를 담을 새로운 배열을 매번 생성해서 리턴하지 않고, 인덱스 접근을 이용해 입력 배열을 계속해서 업데이트 하면 메모리 사용량을 줄일 수 있다. (In-place Sort)

public class Merge {
	public static void mergeSort(int[] arr) {
    	sort(arr, 0, arr.length);
    }
    
    private static void sort(int[] arr, int low, int high) {
    	if (high - low < 2) {
        	return;
        }
        
        int mid = (low + high)/2;	// 중간 위치를 계산하여 리스트를 균등 분할 - 분할(Divide)
        sort(arr, 0, mid);			// 앞쪽 부분 리스트 정렬 - 정복(conquer)
        sort(arr, mid, high);		// 뒤쪽 부분 리스트 정렬 - 정복(conquer)        
        merge(arr, low, mid, high);	// 정렬된 2개의 부분 배열을 합병하는 과정 - 결합(combine)
    }
    
    private static void merge(int[] arr, int low, int mid, int high) {
    	int[] temp = new int[high - low];
        int t = 0, l = low, h = mid;
        
        // 분할 정렬된 arr의 합병
        while (l < mid && h < high) {
        	if (arr[l] < arr[h]) {
            	temp[t++] = arr[l++];
            }
            else {
            	temp[t++] = arr[h++];
            }
        }
        
        // 남아있는 값들을 일괄 복사
        while (l < mid) {
        	temp[t++] = arr[l++];
        }
        
        // 남아 있는 값들을 일괄 복사
        while (h < high) {
        	temp[t++] = arr[h++];
        }
        
        // 임시 배열의 리스트를 배열 arr[]로 재복사
        for (int i = low; i < high; i++) {
        	arr[i] = temp[i - low];
        }
    }
}

복잡도

• 공간복잡도 : 두 개의 배열을 병합할 때 병합 결과를 담아 놓을 배열이 추가로 필요하다. 따라서, 공간 복잡도는 O(N) 이다.
• 시간복잡도 : 전반적인 반복의 수는 점점 절반으로 줄어들기 때문에 O(logN) 시간이 필요하며, 각 패스에서 병합랄 때 모든 값들을 비교해야 하므로 O(N) 시간이 소모된다. 따라서 총 시간 복잡도는 O(NlogN) 이다.