[Algorithm] 2-6 Heap Sort(힙 정렬)

정렬 알고리즘
1. Bubble Sort(거품 정렬)
2. Selection Sort(선택 정렬)
3. Insertion Sort(삽입 정렬)
4. Quick Sort(퀵 정렬)
5. Merge Sort(병합 정렬)
6. Heap Sort(힙 정렬) ⇠
7. Radix Sort(기수 정렬)
8. Counting Sort(계수 정렬)

기본 개념

• 완전 이진 트리를 기본으로 하는 힙(Heap) 자료구조를 기반으로 한 정렬 방식
• 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법이다.
• 불안정 정렬에 속한다.
• 퀵 정렬과 병합 정렬의 성능이 좋기 때문에 힙 정렬의 사용빈도가 높지는 않다.
• 하지만 힙 자료구조가 많이 활용되고 있으며, 이때 함께 따라오는 개념이 힙 정렬이다.

완전 이진 트리
삽입할 때 왼쪽부터 차례대로 추가하는 이진 트리

특징

• 시간 복잡도가 좋은 편이다.
• 힙 정렬이 가장 유용한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 값 몇 개만 필요할 때이다.

힙 소트가 유용할 때

• 가장 크거나 가장 작은 값을 구할 때
  • 최소 힙 or 최대 힙의 루트 값이기 때문에 한번의 힙 구성을 통해 구하는 것이 가능하다.
• 최대 K만큼 떨어진 요소들을 정렬할 때
  • 삽입정렬보다 더욱 개선된 결과를 얻어낼 수 있다.

구현(Java)

과정
1. 정렬해야 할 n개의 요소들을 최대 힙(완전 이진 트리 형태)로 만든다. (내림차순을 기준으로 정렬)
2. 그 다음으로 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤부터 저장한다.
3. 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 된다.

Max Heap 삽입 과정

1. 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
2. 새로운 노드가 부모 노드보다 크면 교환해서 힙의 성질을 만족시킨다.

Max Heap 삭제 과정

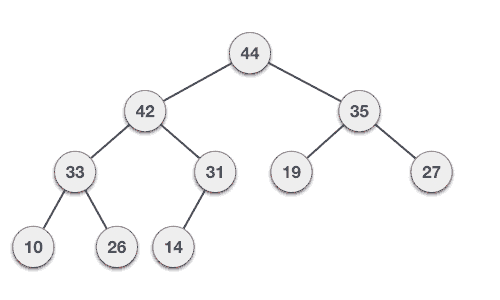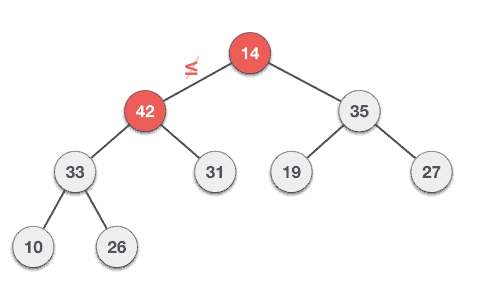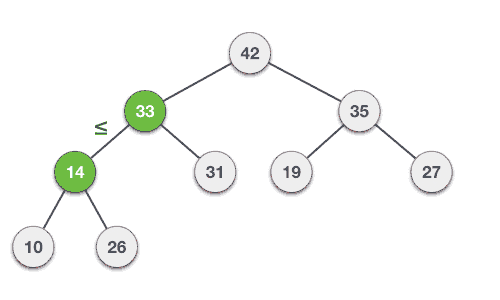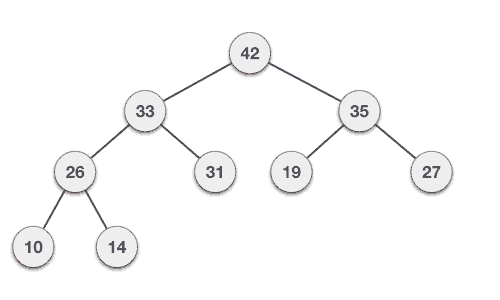
1. 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다. (최대 힙에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.)
2. 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
3. 힙을 재구성한다. (삽입 노드와 자식 노드를 비교하여 자식 노드 중 더 큰 값과 교환을 반복)

코드

private void solve() {
    int[] array = { 230, 10, 60, 550, 40, 220, 20 };
    
    heapSort(array);
}

public static void heapify(int[] array, int n, int i) {
	int p = i;
    int l = i * 2 + 1;
    int r = i * 2 + 2;
    
    if (l < n && array[p] < array[l]) {
    	p = l;
    }
    
    if (r < n && array[p] < array[r]) {
    	p = r;
    }
    
    if (i != p) {
    	swap(array, p, i);
        heapify(array, n, p);
    }
}

public static void heapSort(int[] array) {
	int n = array.length;
    
    // max heap 초기화
    for (int i = n / 2-1; i >= 0; i--) {
    	/* 첫번째 heapify */
    	heapify(array, n, i);
    }
    
    // extract 연산
    for (int i = n - 1; i > 0; i--) {
    	swap(array, 0, i);
        /* 두번째 heapify */
        heapify(array, i, 0);
    }
}

public static void swap(int[] array, int a, int b) {
	int temp = array[a];
    array[a] = array[b];
    array[b] = temp;
}

1번째 heapify

• 일반 배열을 힙으로 구성하는 역할
• 자식 노드로부터 부모 노드 비교
• n/2-1부터 0까지 인덱스가 도는 이유
  • 부모 노드의 인덱스를 기준으로 왼쪽 자식노드(i*2 + 1), 오른쪽 자식노드(i*2 + 2)이기 때문

2번째 heapify

• 요소가 하나 제거된 이후에 다시 최대 힙을 구성하기 위함
• 루트를 기준으로 진행(extract 연산 처리를 위해)

복잡도

• 공간복잡도 : 추가적인 메모리를 필요로하지 않는다. 리스트 안에서 swap 하므로 O(N)이다.
• 시간복잡도 : 힙 트리의 전체 높이가 거의 logN이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 logN만큼 소요된다. 요소의 개수가 N개 이므로 전체적으로 O(NlogN)의 시간이 걸린다.