통계 기초
통계학
- 산술적 방법을 기초하여, 주로 다랴의 데이터를 관찰하고 정리 및 분석하는 방법을 연구하는 수학의 한 분야이다.
- 데이터 → 통계적 분석 → 예측 및 의사 결정
- 기술통계학 : 데이터를 수집하고 수집된 데이터를 쉽게 이해하고 설명할 수 있도록 정리 요약 설명하는 방법론
- 추론통계학 : 모집단으로 부터 추출한 표본 데이터를 분석하여 모집단의 여러가지 특성을 추측하는 방법론

데이터의 이해
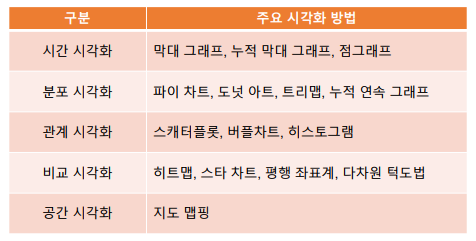
데이터와 그래프
- 변수 (변하는 숫자) : 통계학 → 조사 목적에 따라 관측된 자료값을 변수라 하고 해당 변수에 대하여 관측된 값들이 바로 자료(DATA)가 된다
- 질적 자료 : 범주로 구분하여 표현할 수 있는 데이터 (명목형 변수, 순서형 변수)
- 양적 자료 : 숫자의 형태로 숫자의 크기가 의미를 갖고 있음 (이산형 변수, 연속형 변수)
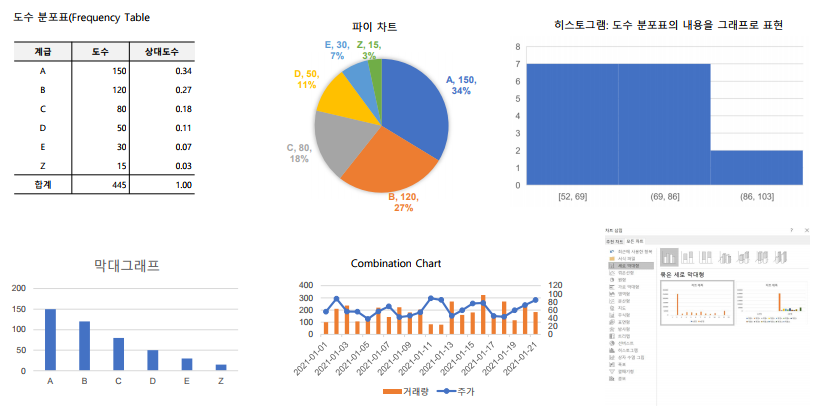
- EDA : 데이터를 분석하는 과정 중에 가장 많이 사용하는 분석 방법이며, 데이터를 탐색하는 분석 방법으로 도표, 그래프, 요약 통계 등을 사용하여 데이터를 체계적으로 분석하는 방법
- 데이터 시각화 : 데이터 분석 결과를 쉽게 이해할 수 있도록 시각적으로 표현하고 전달하는 과정이며, 도표라는 수단을 통해 정보를 명확하고 효과적으로 전달하는 것
데이터의 기초 통계량
- 기초통계량
- 통계량은 표본으로 산출한 값으로 기술 통계량이라고도 표현
- 통계량을 통해 데이터(표본)가 갖는 특성을 이해 할 수 있음
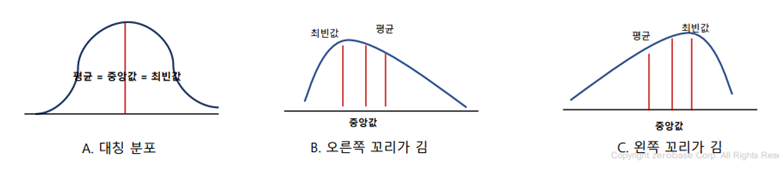
- 중심경향치
- 표본을 이해하기 위해 표본의 중심에 대해 관심을 갖기 때문에 표본의 중심을 설명하는 값을 대표값이라함 ⇒ 중심경향치 (평균, 중앙값, 최빈값, 절사 평균)
- 중앙값 (median)
- 관측치를 크기순으로 나열 했을 때, 가운데 위치하는 값을 의미함
- 이상치가 포함된 데이터에 대해서 사용함
- 최빈값 (mode)
- 관측치 중에 가장 많이 관측되는 값
- 명목형 데이터의 경우 사용
- 산포도
- 데이터가 어떻게 흩어져 있는지 확인하기 위해서 중심경향치와 함께 산포에 대한 측도를 같이 고려해야함
- 데이터의 산포도를 나타내는 측도 : 범위, 사분위수, 분산, 표준편차, 변동 계수
- 범위(range) : 데이터의 최댓값과 최솟값의 차이를 의미함
- 사분위수(quartile) : 전체 데이터를 오름차순으로 정렬하여 4등분하여, 첫 번째를 제1사부위수(Q1), 두 번째를 제2사부위수(Q2), 세 번째를 제3사부위수(Q3)
- 사분위수 범위 (IQR) = Q3 - Q1
- 백분위수(percentile) : 전체 데이터를 오름차순으로 정렬하여 주어진 비율에 의해 등분한 값, 제p백분위수는 p%에 위치한 자료값을 말함
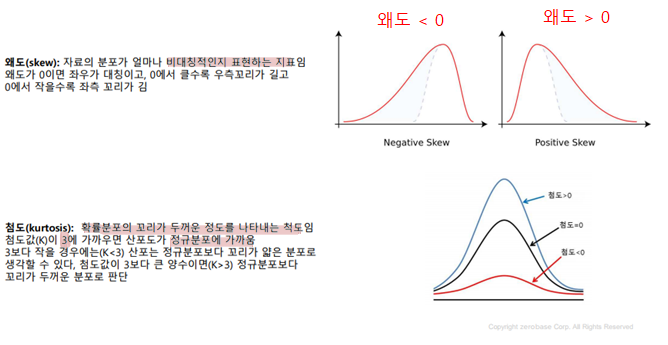
- 분산(variance)
- 데이터의 분포가 얼마나 흩어져 있는지를 알 수 있는 측도 임
- 데이터의 각각의 값들의 편차 제곱합으로 계산하며 수식은 아래와 같음

확률 이론
확률
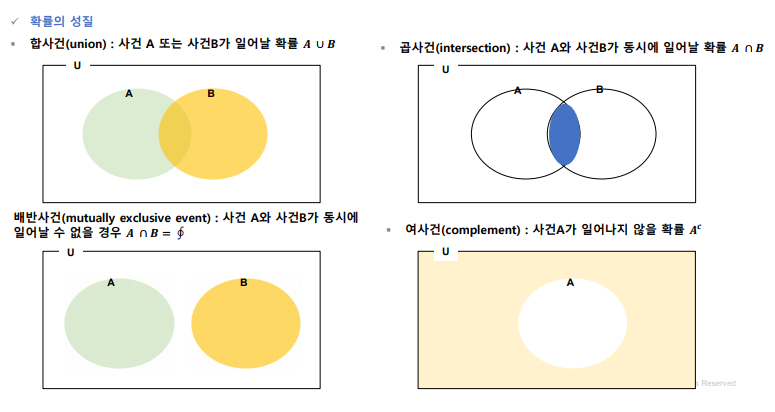
- 확률 : 모든 경우의 수에 대한 특정 사건이 발생하는 비율
- 다른 비율을 나타낼 때처럼 0과 1 사이의 확률에 100을 곱하여 0과 100 사이의 백분율(%)로 나타내거나 옛날처럼 할·푼·리로 나타내기도 한다.
- 표본 공간 : 표본 공간이란 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합
- 통계적 확률 정의


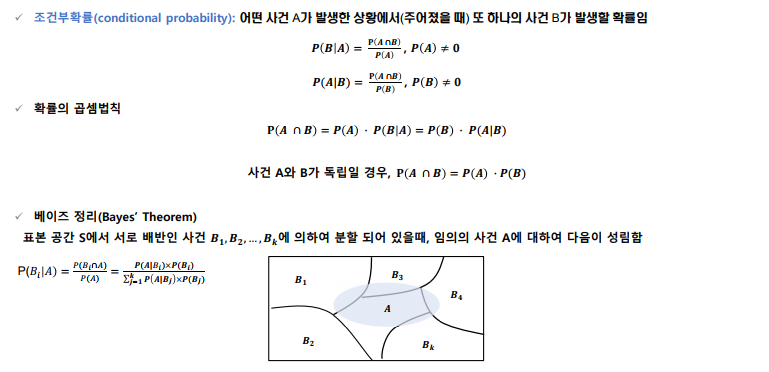
- 조건부 확률
확률 변수
- 확률 변수 : 표본공간에서 각 사건에 실수를 대응시키는 함수를 확률 변수라고 함
- 확률 변수의 값을 하나의 사건에 대하여 하나의 값을 가지며, 실험의 결과에 의하여 변함
- 이산 확률 변수 : 셀 수 있는 값들로 구성되거나 일정 범위로 나타내는 경우
- 연속 확률 변수 : 연속형 또는 무한대와 같이 셀 수 없는 경우




확률 분포
이산형 확률 분포
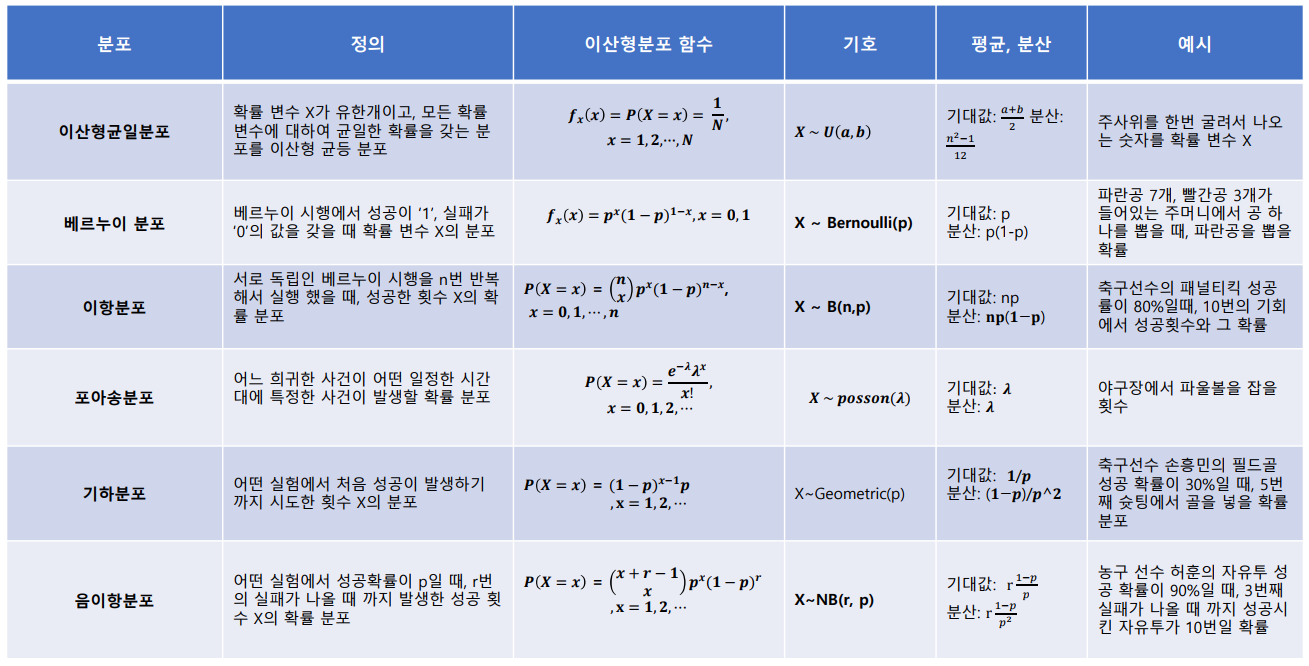
- 확률 분포 : 확률 변수 X가 취할 수 있는 모든 값과 그 값을 나타날 확률을 표현한 함
연속형 확률 분포
-
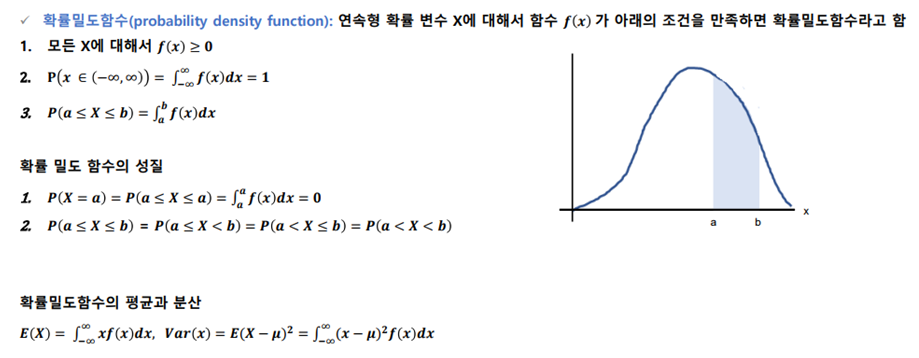
확률 밀도 함수 (pdf)
-
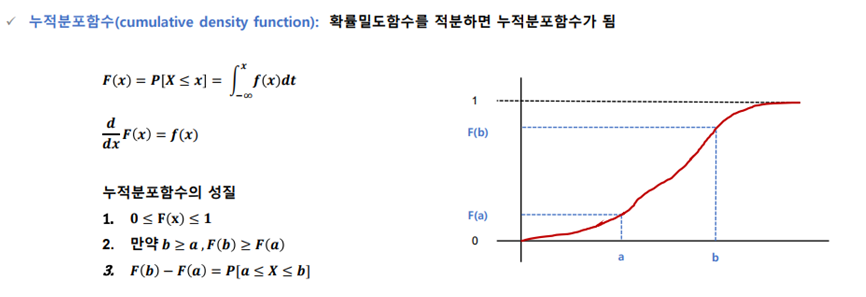
누적 분포 함수 (cdf)
-
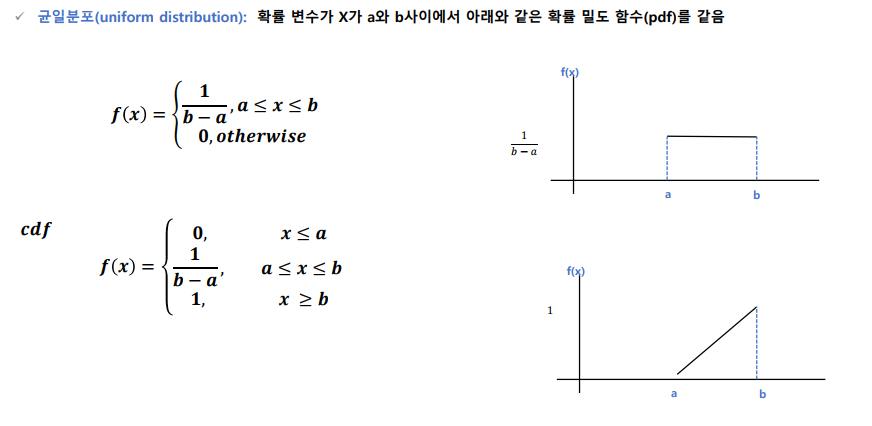
균일 분포
-
균등 분포의 평균, 분산
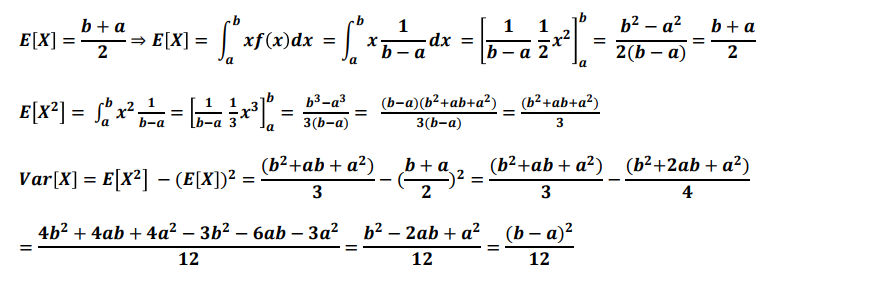
-
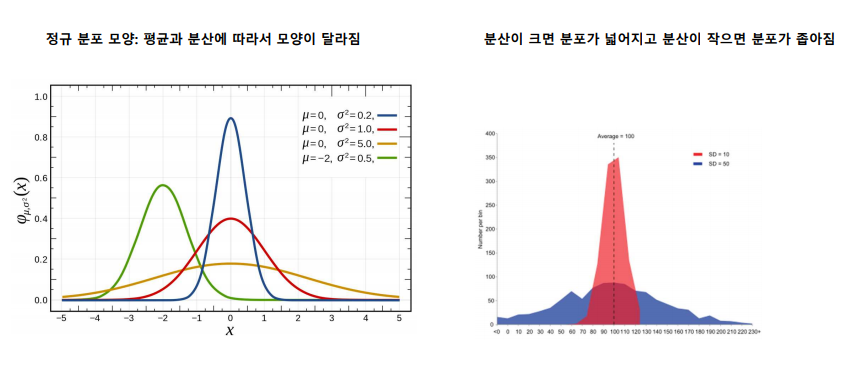
정규 분포 ( = 가우스 분포)
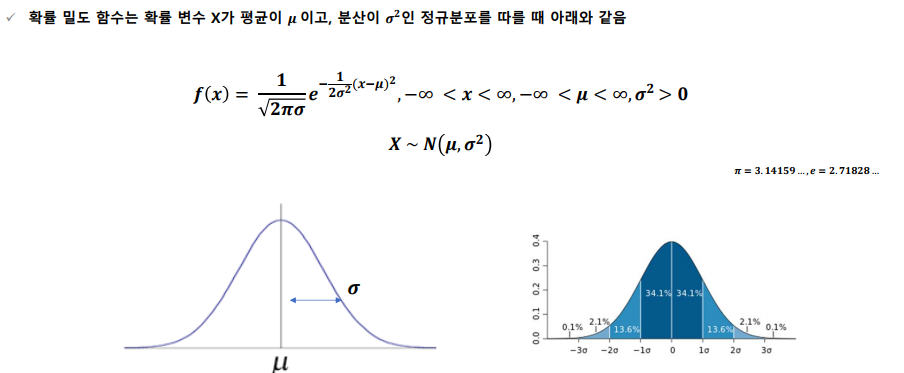
-
정규 분포의 평균과 분산
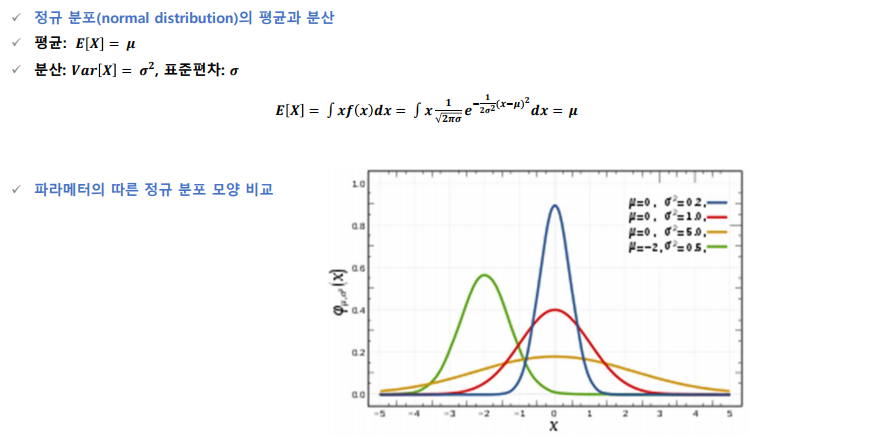
-
표준 정규 분포
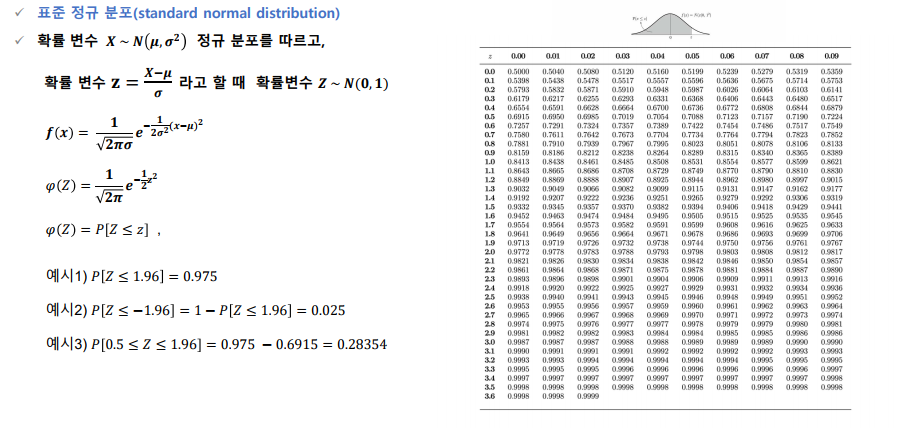
-
정규 분포의 성질
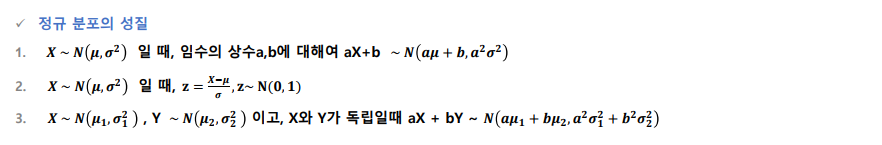
-
이항분포의 정규 근사
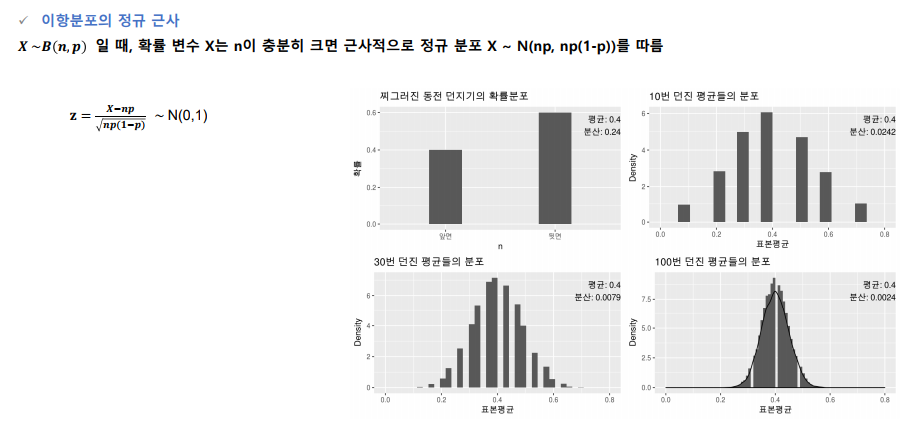
-
지수 분포
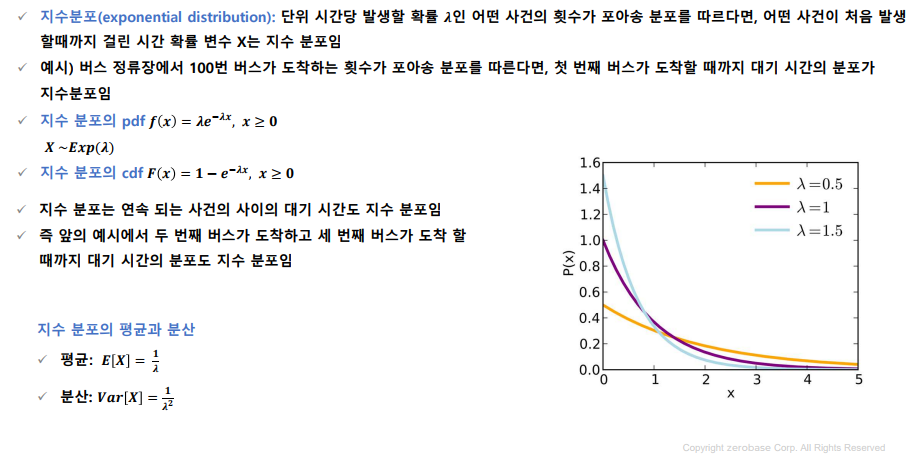
-
지수 분포의 무기억성

"이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.”