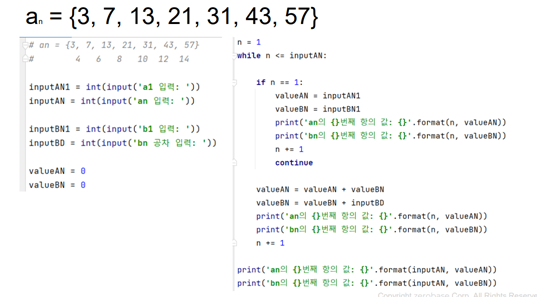
등차 수열, 등비 수열
- 수열 : 규칙성을 가지고 나열되어 있는 수들 (an= 2n / n의 정의역 자연수)
- 항들의 합과 항의 관계 : 특정 항은 특정 항까지의 합에서 특정 항 이전의 항까지의 합과 같다.
- 수열의 합 an =Sn - S(n-1)
- 등차 수열 : 연속된 두 항의 차이가 일정한 수열 ⇒ 등차수열 규칙성을 이용해서 일반항 구할 수 있다. (공차 → d)
- 등차 수열(일반항) 공식 : an = a1 + (n-1) * d
- 등차 중앙 : 연속된 세 항에서 가운데 항
# 등차 수열(일반항) 공식 : an = a1 + (n-1) * d
valueN = inputN1 + (inputN-1) * inputD
print('{}번째 항의 값: {}'.format(inputN, valueN))
# 등차 수열의 (합) 공식 : sn = n(a1+an) / 2
valueN = inputN1 + (inputN - 1) * inputD
sumN = inputN * (inputN1 + valueN) / 2`
- 등비 수열 : 연속된 두 항의 비가 일정한 수열
- 등비 수열 공식 :an = a1 r^(n-1)
- 등비 수열(합) 공식 : sn = a1 (1- r^n) / (1-r)
⇒ 등비수열 규칙성을 이용해서 일반항 구할 수 있다. (공비 → r) - 등비 중앙 : 연속된 세 항에서 가운데
# 등비 수열 공식 :an = a1 * r^(n-1)
valueN = inputN1 * (inputR ** (inputN -1))
#등비 수열(합) 공식 : sn = a1 * (1- r^n) / (1-r)
sumN = inputN1 * (1 - (inputR** inputN )) / (1 - inputR)
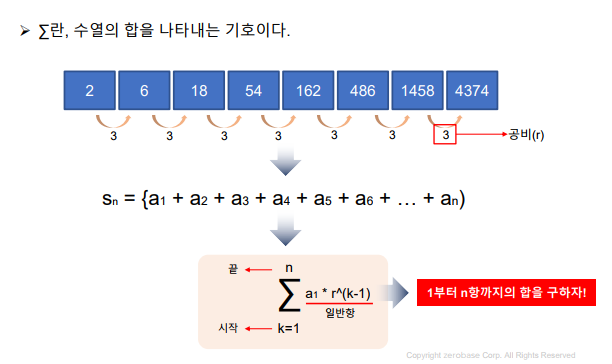
시그마
- 시그마 : 수열의 합을 나타내는 기호
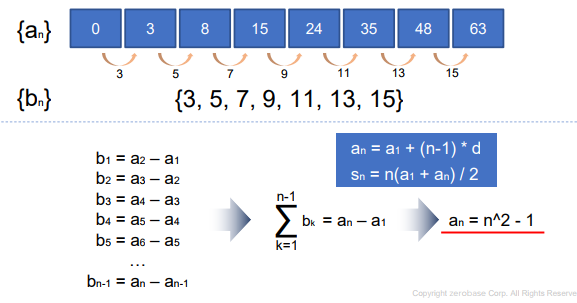
계차 수열
- 계차 수열 : 어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열
⇒ 계차 수열을 이용해서 수열 an의 일반항을 구할 수 있다
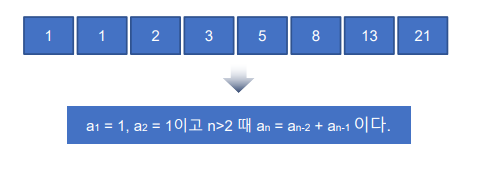
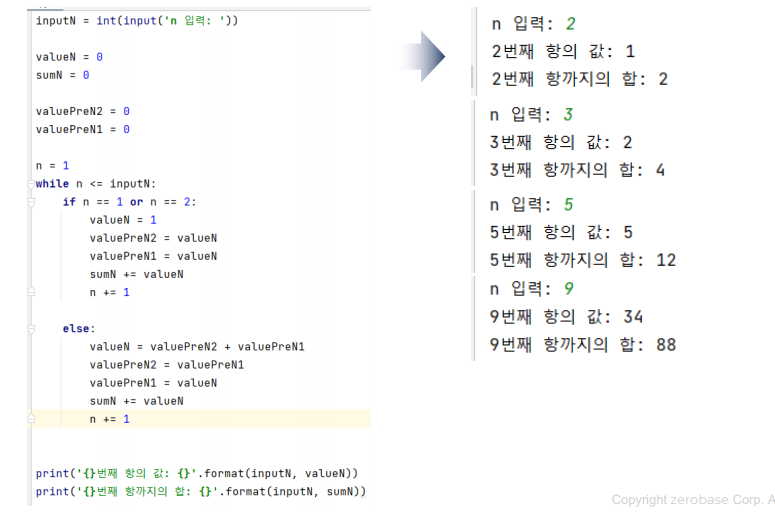
피보나치 수열
- 피보나치 수열 : 세 번째 항은 두 번째 항과 첫 번째 항을 더한 합이다.
“이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다.”