📕 독립변수와 종속변수

독립변수는 쉽게 말해 원인이고 종속변수는 결과라고 할 수 있다.

1. 독립변수 (Independent Variable)

• 독립변수는 다른 변수에 영향을 미치는 변수로, 원인 또는 설명 변수로도 불린다.
• 연구나 분석에서 독립변수는 다른 변수들의 변화를 설명하거나 예측하기 위해 사용된다.
• 독립변수는 실험 또는 연구 디자인에서 조작할 수 있고, 다른 변수들을 분석하는 데 도움이 된다.
• 예를 들어, 어떤 제품의 가격, 광고 비용 및 경쟁 업체의 가격이 제품의 판매량에 영향을 미치는 경우, 이들은 독립변수이다.

2. 종속변수 (Dependent Variable)

• 종속변수는 다른 변수(독립변수)에 의해 영향을 받는 변수로, 결과 변수 또는 응답 변수로도 불린다.
• 연구나 분석에서 종속변수는 분석의 대상이 되며, 독립변수에 따라 변화하는 값을 나타낸다.
• 종속변수는 독립변수의 변화에 따라 변화하며, 이러한 관계를 분석하여 독립변수가 종속변수에 어떻게 영향을 미치는지 이해한다.
• 종속변수의 예시로는 제품의 판매량, 학생들의 성적, 환자의 건강 상태 등이 있다.

독립변수와 종속변수 간의 관계를 분석하는 것은 주로 통계 분석, 회귀 분석, 기계학습, 연구 및 실험 디자인에서 중요한 역할을 한다. 이러한 변수들을 분석하여 원인과 결과, 패턴, 경향 등을 이해하고 예측하는 것이 가능하다.

📕 연속변수와 범주변수

연속변수는 연속적인 수로 수량화가 가능한 자료이고, 범주형 자료는 범주를 서로 구분하는 이름에 해당하는 자료이다.

1. 연속변수 (Continuous Variable)

• 연속변수는 무한한 수의 가능한 값 중에서 어떤 값을 가질 수 있는 변수이다.
• 이러한 변수는 숫자로 표현되며, 정수나 소수점 이하의 값으로 나타날 수 있다.
• 연속변수의 예시로는 연령, 키, 무게, 온도, 시간 등이 있다.
• 연속변수는 연속적인 범위에서 값을 가질 수 있으므로 무한한 가능한 값이 존재할 수 있다.

2. 범주변수 (Categorical Variable)

• 범주변수는 몇 가지 범주 또는 범주로 구분되는 변수이다.
• 이러한 변수는 일반적으로 문자열 또는 정수 값으로 표현된다.
• 범주변수의 예시로는 성별, 학력 수준, 지역, 제품 브랜드, 직위 등이 있다.
• 범주변수는 이산적인 값을 가지며, 범주 간에 분류되거나 그룹화된다.

🔎 척도

통계 및 데이터 분석에서 척도는 데이터의 측정 및 표현 방법을 의미한다. 척도는 데이터를 수치로 표현하는 방법을 나타내며, 데이터의 특성과 분석 방법에 영향을 미친다. 주로 네 가지 주요 척도는 명목척도, 순서척도, 간격척도, 비율척도 이다.
명목척도와 순서척도는 범주변수에 속하고, 간격척도와 비율척도는 연속변수로 간주될 수 있다.

1. 명목척도 (Nominal Scale)

• 명목척도는 데이터를 범주로 분류하는 데 사용된다.
• 범주 간에는 순서나 계량적 의미가 없으며, 데이터를 간단히 분류하기 위해 사용된다.
• 명목척도는 범주 간에 순서나 크기의 의미가 없는 척도이기 때문에 정규분포에 대한 가정을 할 필요가 없다.
• 예시로는 성별, 혈액형, 지역, 제품 브랜드 등이 있다.

2. 순서척도 (Ordinal Scale)

• 순서척도는 명목척도의 특성을 가지면서, 범주 간에 상대적인 순서 또는 순위를 나타내는 데 사용된다.
• 각 범주 사이의 간격이 일정하지 않으며, 순서를 나타내는 명목척도의 확장으로 볼 수 있다.
  • 간격이나 비율에 대한 정보가 없으므로 정규성 검정에서는 일반적으로 비모수적인 방법이 사용됩니다.
• 예시로는 학력 수준(고졸, 대졸, 석사, 박사), 선호도(낮음, 중간, 높음) 등이 있다.

3. 간격척도 (Interval Scale)

• 간격척도는 순서척도의 특성을 가지면서, 간격 간의 일정한 간격이 존재하며, 영점(zero point)이 없는 측정 수준이다.
• 간격척도는 범주 간의 상대적 크기와 순서를 나타내며, 간격의 크기를 비교할 수 있지만, 절대적인 영점이 없어 비율을 계산할 수 없다.
• 간격이 일정하므로 정규성 가정에 가까운 분포를 가질 수 있지만, 아직 비율이 없기 때문에 주의가 필요하다.
• 예시로는 온도(섭씨, 화씨), 시험 점수(점수 간의 간격은 동일하나, 0점은 아무것도 나타내지 않음) 등이 있다.

4. 비율척도 (Ratio Scale)

• 비율척도는 간격척도의 특성을 가지면서, 절대적인 영점(zero point)이 존재하며 비율을 계산할 수 있는 측정 수준이다.
• 데이터의 크기, 순서, 간격 및 비율을 모두 나타낼 수 있으며, 가장 상세한 수치형 변수이다.
• 비율척도는 가장 높은 수준의 측정 수준으로, 정규성 가정에 가까운 분포를 가질 수 있다.
• 예시로는 연령, 무게, 길이, 소득, 거리 등이 있다.

척도에 따라 적용 가능한 통계 분석방법이 달라지기 때문에 척도는 중요하다.

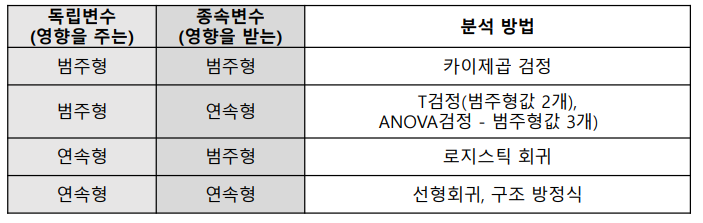
📕 확률변수

확률변수는 특정 확률 분포에 따라 값을 가질 수 있는 변수를 나타낸다. 간단히 말하면, 어떤 확률적인 현상에 대해 수치적으로 표현된 변수이다. 이것은 특정 사건이 발생할 가능성을 나타내는 확률과 연결되어 있다.

확률변수는 크게 두 가지 유형으로 나눌 수 있다.

1. 이산확률변수 (Discrete Random Variable)

• 이산확률변수는 가능한 값들이 이산적인(불연속적인) 경우를 나타낸다.
• 이산확률변수의 값들은 보통 정수이며, 예시로는 동전 던지기에서 나오는 앞면의 횟수, 주사위 던지기에서 나오는 눈의 수 등이 있다.
• 확률질량함수(probability mass function, PMF)를 통해 각 값에 대한 확률을 나타낼 수 있다.

2. 연속확률변수 (Continuous Random Variable)

• 연속확률변수는 가능한 값들이 연속적인(무한히 많은) 경우를 나타낸다.
• 연속확률변수의 값들은 실수의 범위에 속하며, 예시로는 온도, 시간, 길이 등이 있다.
• 확률밀도함수(probability density function, PDF)를 통해 값의 밀도를 나타낼 수 있다.

확률변수는 일반적으로 대문자로 표기되며, 특정 값은 소문자로 표기됩니다. 예를 들어, 이산확률변수 X에서 특정 값 x의 확률은 P(X = x)로 표기된다.