📕 개념

📎 ANOVA란?

ANOVA(Analysis of Variance)란? 세 개 이상의 그룹 간의 평균 차이를 비교하는 통계적인 방법이다. ANOVA는 그룹 간의 평균 차이가 통계적으로 유의미한지를 검정한다. 독립변수로는 범주형, 종속변수로는 연속형 변수를 사용한다.
ANOVA를 한국말로 해석해보면 분산 분석이라는 뜻이다. 분산분석이라는 용어는 분산이 발생한 과정을 분석하여 요인에 의한 분산과 요인을 통해 나누어진 각 집단 내의 분산으로 나누고 요인에 의한 분산이 의미 있는 크기를 가지는지를 검정하는 것을 의미한다.
세 집단 이상의 평균비교에서 독립인 두 집단의 평균 비교를 반복하여 실시한 경우에 제 1종 오류가 증가하게 되어 문제가 발생한다.
이를 해결하기 위해 Fisher가 개발한 것이 바로 분산분석(ANOVA, Analysis Of Variance)이다.

⭐ f-value

f-value는 anova분석에 있어 중요한 지표이다. f-value는 분자 부분의 분산을 비교 대상인 분모 부분의 분산과 비교하여 비율로써 나타낸 값이다.
f-value는 그룹 간의 변동과 그룹 내의 변동을 비교하여 통계적 유의성을 판단하는 데 사용된다. f값은 ANOVA 검정의 결과 중 하나로, 그룹 간의 평균 차이가 우연에 의한 것인지를 확인하는 데 도움이 된다.

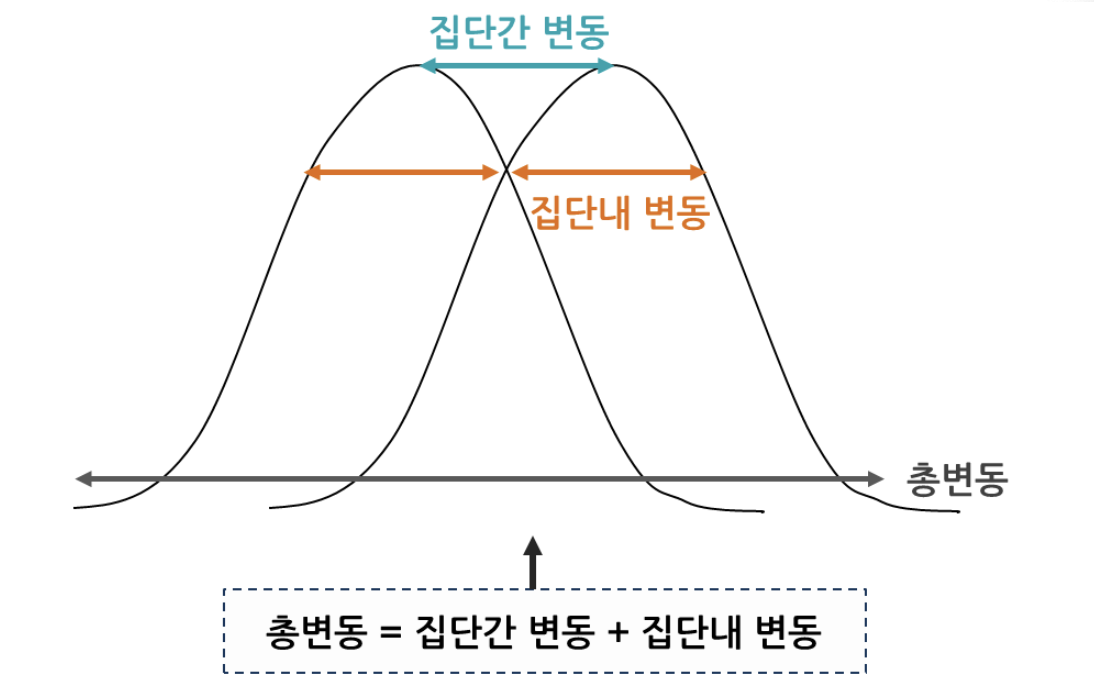
여러 그룹 간의 평균 차이를 비교할 때, ANOVA는 다음 두 가지 변동을 고려한다.

1. 그룹 간 변동 (Between-Group Variation)

각 그룹의 평균 값이 전체 평균에서 얼마나 멀리 떨어져 있는지 측정한다.

2. 그룹 내 변동 (Within-Group Variation)

각 그룹 내에서 개별 관측치가 해당 그룹의 평균에서 얼마나 멀리 떨어져 있는지 측정한다.

f값 = 그룹 간 분산(Between Variance) / 그룹 내 분산(Within Variance)

f값을 구하는 수식은 위와 같다.
f값은 Between-Group Variation과 Within-Group Variation 간의 비율로 계산된다. 높은 f값은 그룹 간의 평균 차이가 통계적으로 유의미할 가능성이 높다는 것을 나타낸다.

f값이 크면서 p-value가 작으면, 그룹 간의 평균 차이가 우연에 의한 것이 아니라고 판단할 수 있다. 따라서 귀무가설을 기각하고 대립가설을 채택하게 된다. 이는 적어도 하나의 그룹이 다른 그룹들과 다르다는 것을 의미한다.

통상적으로, ANOVA의 결과를 해석할 때는 f값과 함께 p-value를 고려하여야 한다. p-value가 유의수준(일반적으로 0.05)보다 작으면, 그룹 간의 차이가 통계적으로 유의미하다고 판단할 수 있다.

📎 전제조건

독립성 : 각 집단은 서로 독립이어야 한다.
정규성 : 각 집단은 정규분포를 따라야 한다.
불편성(등분산성) : 각 집단은 서로 분산이 일정해야 한다.

ANOVA검정은 위의 전제조건을 따라야 의미가 있다.
독립성은 상관관계로 확인이 가능하고, 정규성은 shapiro, stats.ks_2samp(콜모고로프-스미르노프(Kolomoforov-smirnov;ks)검정으로 확인 가능하다.
shapiro, stats.ks_2samp은 각 표본이 같은 분포를 따르는지를 확인할 수 있는 방법이다.

📎 사후분석

사후분석(post hoc)이란? ANOVA에서 통계적으로 유의한 그룹 간 차이를 확인했을 때, 어떤 그룹들 간에 구체적으로 차이가 있는지를 판단하기 위해 사용되는 것이 사후검정(Post-hoc test)이다.
ANOVA는 세 개 이상의 그룹 간 평균 차이를 확인할 수 있지만, 어떤 그룹들 간에 차이가 있는지에 대한 정보는 제공하지 않는다. 그렇기 때문에 사후분석을 사용하는 것이다.
주요한 사후검정 방법 중 몇 가지를 알아보았다.

1. Tukey's Honestly Significant Difference (HSD)

• 모든 가능한 그룹 쌍을 비교하여 평균 차이의 통계적 유의성을 평가한다.
• 대표적인 사후검정 방법 중 하나이며, 그룹 간 차이를 정확하게 비교할 수 있다.

2. Bonferroni Correction

• 모든 가능한 그룹 쌍을 비교하면서 유의수준을 보정하여 사용한다.
• 보정된 유의수준은 더 엄격하므로, 1종 오류를 줄이는 데 도움이 된다.

3. Sidak Correction

• Bonferroni와 유사하게 유의수준을 보정하여 사용하지만, 계산 방법이 다르다.
• 보정된 유의수준을 계산할 때 Sidak 공식을 사용한다.

4. Dunnett's Test

• 특정 그룹을 기준으로 다른 모든 그룹을 비교하는 방법이다.
• 일반적으로 특정 그룹이 통제 그룹인 경우에 사용된다.

5. Holm's Method

• 다수의 비교에서 각 비교의 유의성을 조정하는 방법 중 하나이다.
• 각 비교의 p-value를 오름차순으로 정렬하고, 유의수준을 각 비교에 적용하는 방식으로 조정한다.

사후검정은 과도한 유의성 검정을 피하기 위해 주의해야 합니다. 즉, 많은 그룹 간 비교를 수행할수록 1종 오류가 발생할 확률이 높아지므로, 적절한 보정을 사용하여 유의성 수준을 조절하는 것이 중요하다.

📕 종류와 실습

1. 일원배치분산분석(One-Way ANOVA)

• 한 가지 독립 변수(그룹)에 대한 종속 변수(측정 값)의 평균 차이를 비교한다.

🔎 코드예제

다음은 강남구에 있는 GS 편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 있는가?를 분석하는 코드이다.
데이터는 https://raw.githubusercontent.com/pykwon/python/master/testdata_utf8/group3.txt를 이용하였다.
가설은 다음과 같다.

귀무 : GS 편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 없다.
대립 : GS 편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 있다.

import numpy as np 
import pandas as pd 
import scipy.stats as stats
import urllib.request 
from statsmodels.formula.api import ols 
import matplotlib.pyplot as plt 
import statsmodels.api as sm 
from statsmodels.stats.multicomp import pairwise_tukeyhsd
from statsmodels.stats.anova import anova_lm

url = 'https://raw.githubusercontent.com/pykwon/python/master/testdata_utf8/group3.txt'
# data = pd.read_csv(url, header=None)
# print(data.head(3), data.shape)

data = np.genfromtxt(urllib.request.urlopen(url), delimiter=',')
print(data, type(data)) # <class 'numpy.ndarray'>
print(data.shape) # (22, 2)

gr1 = data[data[:,1]==1, 0]
gr2 = data[data[:,1]==2, 0]
gr3 = data[data[:,1]==3, 0]
print(gr1,' ',np.mean(gr1)) # 316.625
print(gr2,' ',np.mean(gr2)) # 256.44444444444446
print(gr3,' ',np.mean(gr3)) # 278.0

print('\n정규성 확인')
print(stats.shapiro(gr1).pvalue)
print(stats.shapiro(gr2).pvalue)
print(stats.shapiro(gr3).pvalue)
# 다 정규성 만족함

print('\n등분산성 확인')
print(stats.levene(gr1,gr2,gr3).pvalue)
print(stats.bartlett(gr1,gr2,gr3).pvalue) 
# 다 등분산성 만족함

# 데이터 산포도(퍼짐정도) 시각화
plt.boxplot([gr1,gr2,gr3], showmeans=True)
plt.show()

# 일원분산분석 처리 방법1
df = pd.DataFrame(data, columns=['pay','group'])
print(df)
lmodel = ols('pay ~ C(group)', data=df).fit() 
print(anova_lm(lmodel,typ=1)) 

print()
# 일원분산분석 처리 방법2
f_statistic, p_value = stats.f_oneway(gr1,gr2,gr3)
print('f_statistic: {} , p_value:{}'.format(f_statistic, p_value))
# f_statistic: 3.7113359882669763 , p_value:0.043589334959178244 => 위와 결과 같음

# 사후 검정
tkResult = pairwise_tukeyhsd(endog=df.pay, groups=df.group)
print(tkResult) # reject True : group1과 group2 차이 있음

tkResult.plot_simultaneous(xlabel='mean', ylabel='group')
plt.show()

🔎 코드 해석

불러온 데이터를 지역1, 지역2, 지역3을 기준으로 gr1, gr2, gr3으로 나누었다. 이 세그룹의 평균을 보면 순서대로 316.625, 256.44444444444446, 278.0인데 이 차이는 유의미한 차이일지 한번 알아보자.

anova 검정을 하기 전 정규성과 등분산성을 만족하는지 검정을 해보았다.

정규성 검정은 shapiro 또는 ks_2samp를 사용하면 되는데 shapiro는 한 개의 변수, ks_2samp는 두개의 변수를 사용해야한다. 검정 결과, 0.05가 넘기 때문에 정규성을 만족한다.
정규성을 만족하면 anova, 만족하지 않으면 kruskal-wallis test를 사용하면 된다.

등분산성 검정은 levene또는 bartlett를 사용하면 되는데 levene은 모수 검정일때 bartlett은 비모수 검정일 때 즉 30개 이하의 작은 집단일 때 사용해야 한다. 검정 결과, 0.05보다 크므로 등분산성 만족한다. 참고로, 등분산성을 만족하지 않은 경우 대처 방법으로는 데이터를 normalization(정규화)으로 처리 또는 standardization(표준화)로 처리, transformation 경우에 따라 자연 log를 붙이기 등이 있다.

방법1 : Statsmodels를 활용한 일원분산분석
ols('pay ~ C(group)', data=df)는 종속 변수 'pay'와 범주형 독립 변수 'group' 간의 선형 회귀 모델을 설정한다.
.fit()은 모델을 학습시킨다.
anova_lm(lmodel, typ=1)은 Statsmodels에서 일원분산분석을 수행하고 그 결과를 출력한다.
typ=1은 Type 1을 사용하라는 옵션으로, 그룹의 순서에 따라 설명변수의 합이 변하는 방식을 나타낸다.
결과에서 p-value가 0.043589으로 유의수준 0.05보다 작기 때문에 귀무가설을 기각한다. 따라서 GS 편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 하나 이상의 그룹에서 있다고 볼수 있다.

방법2 : Scipy를 활용한 일원분산분석
stats.f_oneway() 함수를 사용하여 Scipy를 이용한 일원분산분석을 수행한다.
f_statistic은 F-통계량을 나타내고, p_value는 p-value를 나타낸다.
결과에서 F-통계량은 3.7113359882669763이며, p-value는 0.043589334959178244로 나타납니다. p-vlaue가 0.05보다 작기 때문에 귀무가설을 기각합니다. 따라서 GS 편의점 3개 지역 알바생의 급여에 대한 평균에 차이가 하나 이상의 그룹에서 있다고 볼수 있다. 첫번째 방법과 일치한 결과가 나왔다.

사후검정
pairwise_tukeyhsd 함수를 사용하여 Tukey의 다중 비교를 수행한다.
endog는 종속 변수를 나타내며, 여기서는 'pay'이다.
groups는 그룹을 나타내며, 여기서는 'group'이다.
tkResult에는 Tukey의 다중 비교 결과가 저장되어 있다. 이 결과를 출력하면, 그룹 간의 평균 차이에 대한 여러 정보가 표시됩니다. 특히 reject 열은 해당 그룹 간의 차이가 통계적으로 유의미한지 여부를 나타낸다.

결과를 출력하면 다음과 같은 정보를 확인할 수 있다.

group1과 group2 간에는 차이가 있다(reject=True).
group1과 group3 간에는 차이가 없다(reject=False).
group2와 group3 간에는 차이가 없다(reject=False).
여기서 reject=True는 해당 그룹 간의 평균 차이가 통계적으로 유의미하다는 것을 의미한다. 따라서 group1와 group2 간에는 통계적으로 유의한 평균 차이가 있다고 결론내릴 수 있다.

2. 이원배치분산분석(Two-Way ANOVA)

• 이원분산 분석은 요인이 복수이며, 각 요인의 레벨(그룹)도 복수이다.
• 두 개의 독립 변수가 종속 변수에 평균에 영향을 주는지를 검정한다.
• 각각의 독립 변수에 대해 주 효과와 상호작용 효과를 검토할 수 있다. 가설은 주효과 2개, 교호작용 1개가 나온다.

주효과와 교호효과는 두 개의 요인(독립 변수)이 데이터에 미치는 영향을 이해하고자 하는 데 중요한 개념이다.

📎 주효과(Hypothesis for Main Effects)

1. 첫 번째 요인 (Factor A)의 주효과

• 귀무가설 (H_0): 첫 번째 요인의 수준 간에 종속 변수의 평균에 차이가 없다.
• 대립가설 (H_1): 적어도 하나의 첫 번째 요인의 수준 간에 종속 변수의 평균에 차이가 있다.

2. 두 번째 요인 (Factor B)의 주효과

• 귀무가설 (H_0): 두 번째 요인의 수준 간에 종속 변수의 평균에 차이가 없다.
• 대립가설 (H_1): 적어도 하나의 두 번째 요인의 수준 간에 종속 변수의 평균에 차이가 있다.

📎 교호효과(Hypothesis for Interaction Effects)

교호효과 가설이란, 두 요인 간의 상호 작용(Interaction)이 있는지 확인하기 위한 가설이다. 교호효과는 두 요인이 함께 적용될 때 종속 변수에 미치는 영향을 나타낸다.

- 교호효과 가설

• 귀무가설 (H_0): 두 요인 간의 교호작용 효과가 없다.
• 대립가설 (H_1): 두 요인 간의 교호작용 효과가 있다.

- 해석

• 주효과의 유의성 검정이 통계적으로 유의하다면, 해당 요인의 적어도 하나의 수준 간에 종속 변수의 평균 차이가 있음을 나타낸다.

• 교호효과의 유의성 검정이 통계적으로 유의하다면, 두 요인 간의 조합에 따라 종속 변수의 평균에 차이가 있음을 나타낸다.

  🔎 코드예제

  태아수와 관측자수가 태아의 머리둘레 평균에 영향을 주는가?

  가설은 다음과 같다.

  주효과 가설
  귀무 : 태아수와 태아의 머리둘레 평균은 차이가 없다.
  대립 : 태아수와 태아의 머리둘레 평균은 차이가 있다.
  귀무 : 관측자수와 태아의 머리둘레 평균은 차이가 없다.
  대립 : 관측자수와 태아의 머리둘레 평균은 차이가 있다.
  
  
  교호작용 가설
  귀무 : 교호작용이 없다.(태아수와 관측자수는 관련이 없다 -> 서로 독립적이다.)
  대립 : 교호작용이 있다.(태아수와 관측자수는 관련이 있다 -> 서로 독립적이지 않다.)

import numpy as np 
import pandas as pd 
import scipy.stats as stats
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
plt.rc('font',family='malgun gothic')

#데이터 불러오기
data = pd.read_csv('../testdata/group3_2.txt')

# 데이터 확인
print(data.head(3), data.shape) # 36행 3열
print(data['태아수'].unique()) # [1 2 3]
print(data['관측자수'].unique()) # [1 2 3 4]

# 상자 그림 시각화 - 이상치 등을 확인하기 위해
data.boxplot(column='머리둘레', by='태아수')
plt.show()
data.boxplot(column='머리둘레', by='관측자수')
plt.show()

# 이원배치분산분석 수행
reg = ols("머리둘레~C(태아수)*C(관측자수)",data=data).fit() # 교호작용 확인 o
result=anova_lm(reg, typ=2)
print(result)
#               sum_sq    df            F        PR(>F)
# C(태아수)    324.008889   2.0  2023.182239  1.006291e-32 < 0.05 귀무가설 기각 
# C(관측자수)     1.198611   3.0     4.989593  6.316641e-03 > 0.05 귀무가설 기각 실패
# C(태아수):C(관측자수)    0.562222   6.0     1.222222  3.295509e-01 > 0.05 귀무가설 기각 실패

🔎 코드 해석

ols 함수를 사용하여 이원배치분산분석 모델을 설정한다. 교호작용을 확인하기 위해 C(태아수)*C(관측자수) 형태로 설정하였다. fit()을 통해 모델을 학습시킨다.

reg = ols("머리둘레~C(태아수)+C(관측자수)+C(태아수):C(관측자수)",data=data).fit() # 교호작용 확인 o
reg = ols("머리둘레~C(태아수)+C(관측자수)",data=data).fit() # 교호작용 확인 x

교호작용을 확인하고 확인하지 않고에 따라 코드가 달라질 수 있다.

anova_lm 함수를 사용하여 분산분석을 수행하고 결과를 출력한다.

C(태아수):
p-value < 0.05 이므로 귀무가설을 기각한다. 따라서 적어도 하나의 태아수 수준 간 머리둘레의 평균에 차이가 있음을 나타낸다.

C(관측자수):
p-value > 0.05 이므로 귀무가설을 기각에 실패했다(귀무 채택). 따라서 관측자수 수준 간 머리둘레의 평균에는 차이가 없다고 할 수 있다.

C(태아수):C(관측자수) (교호작용):
p-value > 0.05 이므로 귀무가설을 기각에 실패했다(귀무 채택). 따라서 태아수와 관측자수 간의 교호작용이 머리둘레에 미치는 영향은 통계적으로 유의하지 않다고 할 수 있다.

3. 분산분석의 중복측정(Repeated Measures ANOVA)

• 동일한 피험자 또는 대상의 여러 측정 값에 대한 차이를 분석한다.
• 시간에 따른 변화 또는 동일한 대상에 대한 여러 실험 조건의 효과를 평가할 때 사용된다.

4. 다변량분산분석(MANOVA)

• 둘 이상의 종속 변수에 대한 평균 차이를 검정한다.
• 여러 종속 변수 간의 상호작용이 있는 경우 유용하게 사용된다.

5. 공분산분석(ANCOVA - Analysis of Covariance)

• ANOVA와 회귀 분석을 결합한 분석 방법으로, 일반적으로 두 개의 독립 변수와 하나의 종속 변수를 다룬다.
• 그룹 간의 평균 차이를 비교하면서 동시에 연속적인 변인(공변량)의 영향을 제어할 수 있다.
  
  
  
  이러한 ANOVA의 종류는 다양한 실험 설계와 분석 요구 사항에 따라 선택된다.

그룹내 그룹간 변동 이미지 : https://bokyeong-kim.github.io/data/statistics/2020/02/29/statistics_basic%285%29.html