이항 검정

혜쿰·2023년 11월 13일

📕 개념

결과가 두가지 값을 가지는 확률변수의 분포를 판단하기에 효과적인 검정방법이다. 이항검정을 알아보기에 앞서, 이항분포에 대해 먼저 알아봐야한다.

📎 이항 분포란?

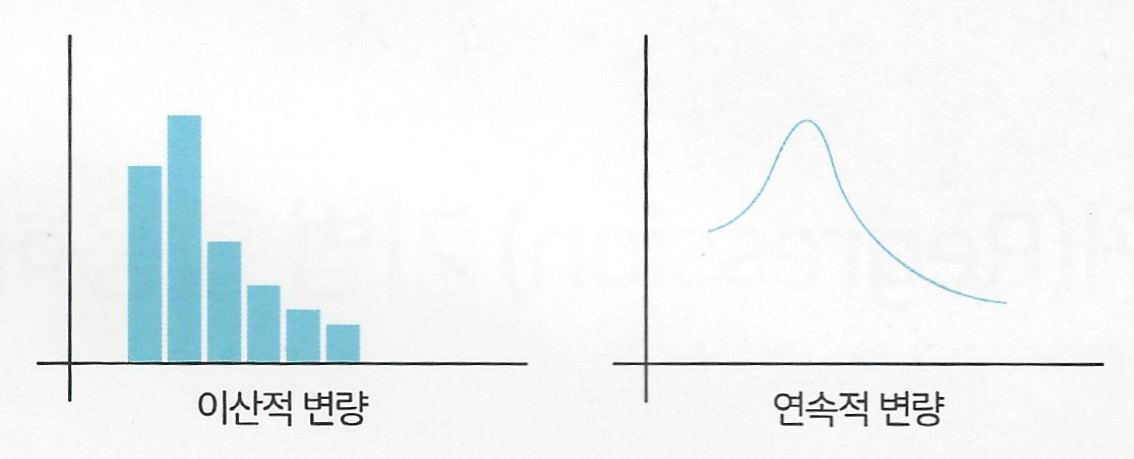
이항 분포(Binomial Distribution)란, 두 가지 결과만 가능한 실험에서 각 시행이 독립적이고 각 시행의 성공 확률이 동일한 경우 나타나는 확률 분포이다. 정규분포는 연속변량인데 반해 이항분포는 이산변량을 사용한다.

이산변량(Discrete Variable)과 연속변량(Continuous Variable)에 대해 조금 알아보고 다음 내용을 공부해보자.

이산변량과 연속변량

1. 이산변량 (Discrete Variable)

정의
이산변량은 셀 수 있는 값을 가지는 변수로, 각각의 값 사이에 간격이 없거나 불연속적인 값을 가지는 변수이다. 주로 정수 값으로 표현되며, 특정 범주에 속하는 것이 특징이다.

특징

정수 값만 가질 수 있음.

각 값 사이에 간격이 없거나 불연속적.

막대 그래프나 히스토그램으로 표현됨.

예시

동전 던지기에서 앞면이 나오는 횟수

주사위 던지기에서 나오는 눈의 수

학생 수, 자동차의 대수 등

2. 연속변량 (Continuous Variable)

정의
연속변량은 셀 수 없는 무한한 범위의 값을 가지는 변수로, 연속적인 값을 가지며 간격이 존재한다. 실수 값을 가질 수 있다.

특징

어떤 두 값 사이에도 무수히 많은 가능한 값을 가짐.

연속된 범위 내의 모든 값이 가능.

히스토그램, 선 그래프 등으로 표현됨.

예시

사람의 키, 몸무게

온도, 시간

속도, 거리 등

정리

이산변량은 정수 값만 가지며 값 사이에 간격이 없거나 불연속적이고, 연속변량은 실수 값을 가지며 값 사이에 간격이 있고 무한한 범위를 갖는다. 이 두 유형의 변수는 통계 분석 및 시각화에서 다르게 다루어지며, 데이터의 특성에 따라 선택되어야 한다.

확률 질량 함수

이항 분포의 확률 질량 함수는 다음과 같다.

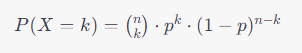
(n)은 시행 횟수,
(k)는 성공 횟수,
(p)는 각 시행에서의 성공 확률,
({n}/{k})는 조합을 나타냅니다.

이항분포에 대한 설명은 여기까지 하고 더 자세히 알고 싶으면 이사이트를 추천한다. -> 링크

📎 이항 검정이란?

이항 검정이란, 두 개의 범주가 있는 이항 분포에 기반하여 주어진 표본에서 모집단의 비율에 대한 가설을 검정하는 통계적인 방법이다. 주로 범주형 데이터에서 두 범주 간의 차이를 확인하거나, 비율이 특정 값과 같은지 여부를 판단할 때 사용된다.

주요 단계

1. 가설 설정

귀무가설 (H_0): 모집단의 비율은 특정 값과 같다.
대립가설 (H_1): 모집단의 비율은 특정 값과 다르다 (양측 검정) 또는 특정 값보다 크거나 작다 (단측 검정).

2. 검정 통계량 계산

주어진 데이터에서 적절한 검정 통계량을 계산한다. 보통은 이항 분포를 사용하여 기대값과 분산을 계산한다.

3. 유의수준 설정

유의수준을 결정하고, 양측 검정인 경우는 해당 확률의 양측 값을, 단측 검정인 경우는 해당 확률의 한 측 값을 계산한다.

4. 결정

계산된 p-value를 유의수준과 비교하여 귀무가설을 기각하거나 기각하지 않는다.

📕 실습

🔎 코드 예제

다음은 "직원을 대상으로 고객대응 교육을 실시하면, 고객안내 서비스 만족률이 높아질까?"에 대한 검정을 하는 코드이다.

귀무 : 직원을 대상으로 고객대응 교육을 실시하면, 고객안내 서비스 만족률이 80%이다.
대립 : 직원을 대상으로 고객대응 교육을 실시하면, 고객안내 서비스 만족률이 80%아니다.

import pandas as pd 
import scipy.stats as stats 

#데이터 불러오기
data = pd.read_csv('../testdata/one_sample.csv')

# 데이터 확인
print(data.head(3)) 
print(data['survey'].unique()) # [1 0]

# 교차표 작성
ctab = pd.crosstab(index=data['survey'], columns='count')
ctab.index = ['불만족','만족']
print(ctab)

# 양측 검정
print('양측 검정 : 방향성이 없다. 기존 80% 만족율 기준으로 실시')
result = stats.binom_test([136,14],p=0.8, alternative='two-sided')  # stats.binom_test(x:성공또는 실패 횟수, N:시도횟수, p:가설확률)
print(result)  

result = stats.binom_test([14,136],p=0.2, alternative='two-sided')
print(result) # 위에 꺼 거꾸로 해도 출력 같음

# 단측 검정
print('단측 검정 : 방향성이 있다.(크다. 작다) 기존 80% 만족율 기준으로 실시')
result = stats.binom_test([136,14],p=0.8, alternative='greater')
print(result) # 귀무기각 실패

result = stats.binom_test([14,136],p=0.2, alternative='less')
print(result) # 위에 꺼 거꾸로 해도 출력 같음

🔎 코드 해석

양측 검정 (Two-Sided Test)
- 데이터에서 만족과 불만족의 빈도를 사용하여 양측 검정을 실시하고 있다.
- stats.binom_test 함수를 사용하여 이항검정을 수행하고 있다. alternative 매개변수에 two-sided를 적어 양측 검정임을 나타낸다.
- 0.0006734701362867024 < 0.05 귀무가설 기각. 따라서, 직원을 대상으로 고객대응 교육을 실시하면, 고객안내 서비스 만족률이 80% 아니다.
단측 검정 (One-Sided Test):
- 방향성이 있는 단측 검정을 실시하고 있다. 크다, 작다로 판별가능 하다.
- stats.binom_test 함수를 사용하여 이항검정을 수행하고 있다. alternative 매개변수에 greater 또는 less를 적어 단측 검정임을 나타낸다.