📕 개념

상관관계 분석은 두 변수 간의 관련성 또는 상호 연관성을 측정하는 통계적인 방법이다. 이 분석은 두 변수가 함께 변화하는 정도를 파악하여 둘 사이의 선형적인 관계의 강도와 방향을 측정한다. 상관관계는 변수 간의 연관성 정도를 나타내며, 인과 관계를 직접적으로 나타내지 않는다.

📎 주요 용어

1. 공분산

공분산(covariance)은 두 변수 간의 관계 강도와 방향을 측정하는 통계적 개념이다. 두 변수가 함께 어떻게 변하는지를 나타내는데 사용된다. 공분산은 두 변수가 함께 증가하는지, 감소하는지, 또는 독립인지를 나타내며, 계산된 값의 부호에 주목해야 한다.

공분산의 수식은 다음과 같다.

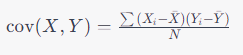
여기서 Xi와 Yi는 각각 변수 X와 Y의 개별적인 관측값이고, Xbar와 Ybar는 각각 X와 Y의 평균값이다. N은 데이터의 총 개수를 나타낸다.

공분산이 양수인 경우, 두 변수는 양의 관계에 있다. 즉, 한 변수가 증가하면 다른 변수도 증가한다. 공분산이 음수인 경우, 두 변수는 음의 관계에 있습니다. 한 변수가 증가하면 다른 변수는 감소한다. 그러나 공분산의 크기만으로는 두 변수 간의 관계의 강도를 파악하기 어려울 수 있다.

공분산의 단점 중 하나는 단위에 따라 크기가 크게 영향을 받는다는 것이다. 그래서 단일 숫자로 비교하기 어렵다. 따라서 표준화된 지표인 피어슨 상관계수를 더 자주 사용하게 됩니다. 상관계수는 공분산을 각 변수의 표준편차로 나눈 값이다. 아래에 설명이 있다.

2. 상관계수 (Correlation Coefficient)

• 상관계수란? 강도와 방향을 나타내는 지표이다. 상관계수는 두 변수 간의 선형적 관계의 강도와 방향을 나타내는 통계적 측도입니다. 두 변수 간의 관계가 얼마나 강한지, 그리고 그 방향이 어떤지를 측정하는 데 사용된다.

• 범위: -1에서 1까지이며, -1은 완전한 음의 상관관계, 1은 완전한 양의 상관관계를 나타냅니다. 0은 상관관계가 없음을 나타낸다.
  양의 상관관계는 한 변수가 증가함에 따라 다른 변수도 증가하는 경우를 말하며, 음의 상관관계는 한 변수가 증가함에 따라 다른 변수는 감소하는 경우를 말한다.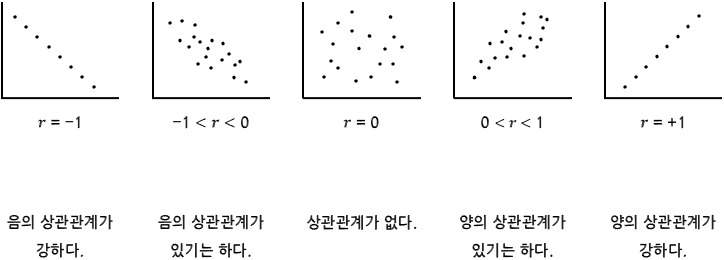

  

상관계수는 두 변수 간의 선형 관계를 측정하므로, 비선형적 관계는 잘 나타내지 못할 수 있다. 그리고 상관관계는 인과관계를 나타내지 않는다. 즉, 두 변수 간의 상관관계가 높다고 해서 한 변수가 다른 변수의 인과관계 라는 것을 의미하지 않습니다.

2-2. 상관계수 종류

상관계수에는 여러 가지 종류가 있지만, 가장 흔하게 사용되는 것은 피어슨 상관계수이다. 여기서는 피어슨 상관계수 외에도 몇 가지 다른 상관계수에 대해 간단히 설명하려고 한다.

1) 피어슨 상관계수(Pearson Correlation Coefficient)

• 가장 널리 사용되는 상관계수 중 하나다.
• 두 변수 간의 선형 관계를 측정한다.

2) 스피어만 순위 상관계수(Spearman Rank Correlation Coefficient)

• 변수 간의 단조 관계를 측정하는데 사용된다.
• 데이터가 선형이 아닌 경우에 유용하다.
• 표본 데이터를 순위로 변환하고, 순위 간의 피어슨 상관계수를 계산한다.

3) 켄달의 타우(Kendall's Tau)

• 변수 간의 순서 관계에 대한 상관계수이다.
• 순서를 비교하고 일치하는 쌍과 불일치하는 쌍을 계산하여 상관계수를 산출한다.

4) 범주형 변수에 대한 상관계수 (Cramer's V)

• 두 범주형 변수 간의 연관성을 측정하는 데 사용된다.
• 피어슨 카이제곱 검정에서 파생되어 범주형 변수 간의 관련성을 보다 강조한다.

이러한 상관계수들은 각자의 사용 사례와 가정이 있으며, 데이터의 특성과 분포에 따라 어떤 상관계수를 선택할지는 상황에 따라 다를 수 있다.

📎 상관관계 분석

상관관계란? 상관관계는 2개 변수가 선형 관계가 있는(상수 비율에서 함께 변경됨을 의미함) 범위를 표현하는 통계적 측도이다. 원인과 결과에 관한 표현 없이 간단한 관계를 설명하는 일반적인 도구이다.

상관관계는 어떻게 측정하기 위해서는 앞서 배웠던 상관계수를 활용한다. 상관계수는 관계의 강도를 수량화한다. 통계적 유의성에 대해서도 상관관계 여부를 검정한다.

상관관계 분석의 제한 사항은 다음과 같다.
상관관계는 탐색되는 2개 변수가 아닌 다른 변수의 존재 또는 효과를 확인할 수 없다. 중요한 것은, 상관관계를 통해 원인 및 결과를 알 수 없다는 것이다. 또한 상관관계는 곡선 관계를 정확하게 설명할 수 없다.

상관관계 분석의 진행

1. 가설 설정:

   • 귀무가설 (H_0): 두 변수 간에는 상관관계가 없다.
   • 대립가설 (H_1): 두 변수 간에는 상관관계가 있다.

2. 데이터 수집:

   • 연구나 조사를 통해 두 변수에 대한 데이터를 수집한다.

3. 상관계수 계산:

   • 피어슨 상관계수 또는 다른 적절한 상관계수를 계산한다.

4. 유의수준 설정:

   • 유의수준을 정하고, 계산된 상관계수의 p-value를 계산한다.

5. 결정:

   • p-value를 유의수준과 비교하여 귀무가설을 기각하거나 기각하지 않는다.
   • 기각된다면, 두 변수 간에는 통계적으로 유의한 상관관계가 있다고 판단한다.

📕 종류와 실습

공분산 & 상관계수

🔎 코드 예시

import numpy as np 

# 공분산
print(np.cov(np.arange(1,6), np.arange(2,7)))   # 2.5
print(np.cov(np.arange(1,6), (3,3,3,3,3)))  # 0
print(np.cov(np.arange(1,6), np.arange(6,1,-1)))    #-2.5

x = [8,3,6,6,9,4,3,9,4,3]
y = [600,200,400,600,900,500,100,800,40,30]
# 시각화
import matplotlib.pyplot as plt 
plt.scatter(x, y)
plt.plot(x,y,'o')
plt.show()

# print('x,y의 공분산 : ',np.cov(x,y))
print('x,y의 공분산 : ',np.cov(x,y)[0,1])

print('x,y의 상관계수 : ',np.corrcoef (x,y))

# 피어슨 상관 계수
m = [-3, -2, -1, 0, 1, 2, 3]
n = [9, 4, 1, 0, 1, 4, 9]
plt.plot(m,n)
plt.show()
print('m, n의 공분산 : ', np.cov(m,n)[0,1])
print('m, n의 상관계수 : ', np.corrcoef(m,n)[0,1])

🔎 코드 해석

이 코드는 NumPy를 사용하여 공분산, 상관계수 등을 계산하고, 그림을 그려 시각적으로 확인하는 예제이다.

1. 공분산 계산

• np.cov 함수를 사용하여 두 변수 간의 공분산을 계산한다.
• 첫 번째 예제에서는 [1, 2, 3, 4, 5]와 [2, 3, 4, 5, 6]의 공분산을 계산하고 있고 결과는 2.5이다.
• 두 번째 예제에서는 [1, 2, 3, 4, 5]와 [3, 3, 3, 3, 3]의 공분산을 계산하고 있고 한 변수가 상수값이므로 공분산은 0이다.
• 세 번째 예제에서는 [1, 2, 3, 4, 5]와 [5, 4, 3, 2, 1]의 공분산을 계산하고 있고 결과는 -2.5이다.

2. 산점도 및 상관계수 계산

• 두 변수 x와 y의 산점도를 plt.scatter와 plt.plot으로 그린다.
• np.cov를 사용하여 두 변수 간의 공분산을 계산하고, np.corrcoef를 사용하여 상관계수를 계산한다.

3. 곡선의 경우 상관계수 비교

• m과 n은 곡선을 이루는 데이터이다. 산점도나 상관계수는 곡선의 형태에 대해서는 의미가 없다. 산점도에서는 일직선적인 관계를 나타내는 것이 아니기 때문에 상관계수가 0으로 나오게 된다.

상관관계 분석

🔎 코드 예시

# 상관관계 문제)
# Advertising.csv 파일을 읽어 tv,radio,newspaper 간의 상관관계를 파악하시오. 
# 그리고 이들의 관계를 heatmap 그래프로 표현하시오. 

import pandas as pd 
import numpy as np 
import matplotlib.pyplot as plt 
plt.rc('font', family='malgun gothic')

# 데이터 불러오기
data = pd.read_csv("../testdata/Advertising.csv")

# 데이터 전처리
data = data.drop(['sales','no'], axis=1)
print(data.head(3), data.shape)

# 상관계수 표로 보기
print(data.corr()) 

# 두개씩 보기
print(np.corrcoef(data.tv, data.radio)) # 0.05480866 -> 다소 높은 상관관계
print(np.corrcoef(data.tv, data.newspaper)) #  0.05664787 -> 다소 높은 상관관계
print(np.corrcoef(data.radio, data.newspaper)) # 0.35410375 -> 낮은 상관관계

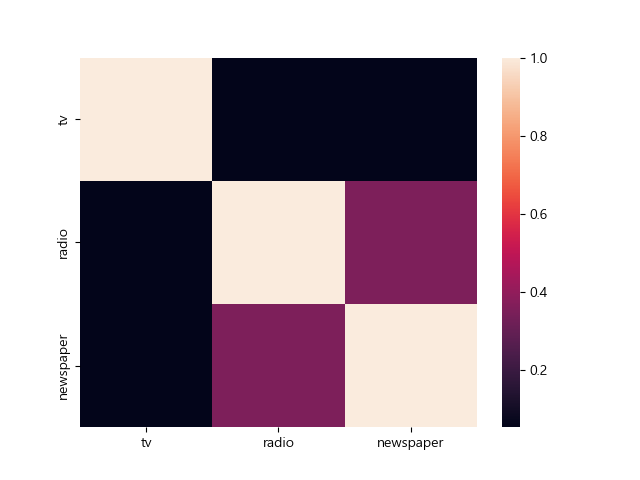
# heatmap
import seaborn as sns 
sns.heatmap(data.corr()) 
plt.show()

🔎 코드 해석

이 코드는 주어진 Advertising.csv 파일에서 TV, Radio, Newspaper 간의 상관관계를 파악하고, 이를 heatmap 그래프로 시각화하는 것을 목적으로 합니다. 코드를 각 부분별로 해석하겠습니다.

두 변수 간의 상관계수 계산 및 출력

corr()는 data에 있는 전체 칼럼(radio, tv, newspaper)의 상관계수를 계산하여 출력한다.
corrcoef()는 두개씩 값을 넣어 상관계수를 계산할 수 있다. 이 코드에서는 'tv'와 'radio', 'tv'와 'newspaper', 'radio'와 'newspaper' 간의 상관계수를 계산하여 출력한다.

Heatmap 그래프 출력

Seaborn 라이브러리를 사용하여 데이터의 상관계수를 heatmap 그래프로 시각화하고 plt.show()를 활용하여 출력한다.
출력 결과는 다음과 같다.

⭐ Heatmap(히트맵)

바로 앞에 나온 히트맵에 대해 알아보자.
히트맵이란, 데이터의 상관관계 또는 패턴을 시각적으로 표현하는 방법 중 하나이다. 주로 행렬 형태의 데이터를 사용하여 값을 색상으로 나타내어 직관적으로 이해하기 쉽다는 특징이 있다.

Heatmap의 주요 특징

1. 색상 표현 : 값의 크기에 따라 색상이 다르게 표현된다. 일반적으로 값이 작을수록 밝은 색상이며, 값이 클수록 진한 색상으로 나타낼 수 있다. 위의 예제의 히트맵은 값에 상관계수를 썼기 때문에 밝은 색상일 수록 상관계수가 작고 진한 색상일 수록 상관계수가 크다고 볼 수 있다.

2. 데이터 행렬 형태 : 히트맵은 데이터를 2차원 행렬 형태로 나타낸다. 각 행과 열은 데이터의 변수를 나타내고, 각 셀은 두 변수 간의 관계를 나타낸다.

3. 시각적인 인사이트 제공 : 히트맵은 복잡한 데이터 패턴을 시각적으로 파악하기 용이하게 만들어준다. 특히 상관관계 행렬을 히트맵으로 나타내면 변수 간의 강도와 방향성을 한눈에 파악할 수 있다. 그렇기 때문에 위의 예제에서 히트맵을 사용한 것이다.

상관계수 이미지 출처 : https://math100.tistory.com/110
상관관계 참고 : https://www.jmp.com/ko_kr/statistics-knowledge-portal/what-is-correlation.html