Chap4 정렬

jade·2025년 2월 13일

DoIt_Algorithm_C++

목록 보기
3/7
post-thumbnail

1. 버블정렬

1) 개념

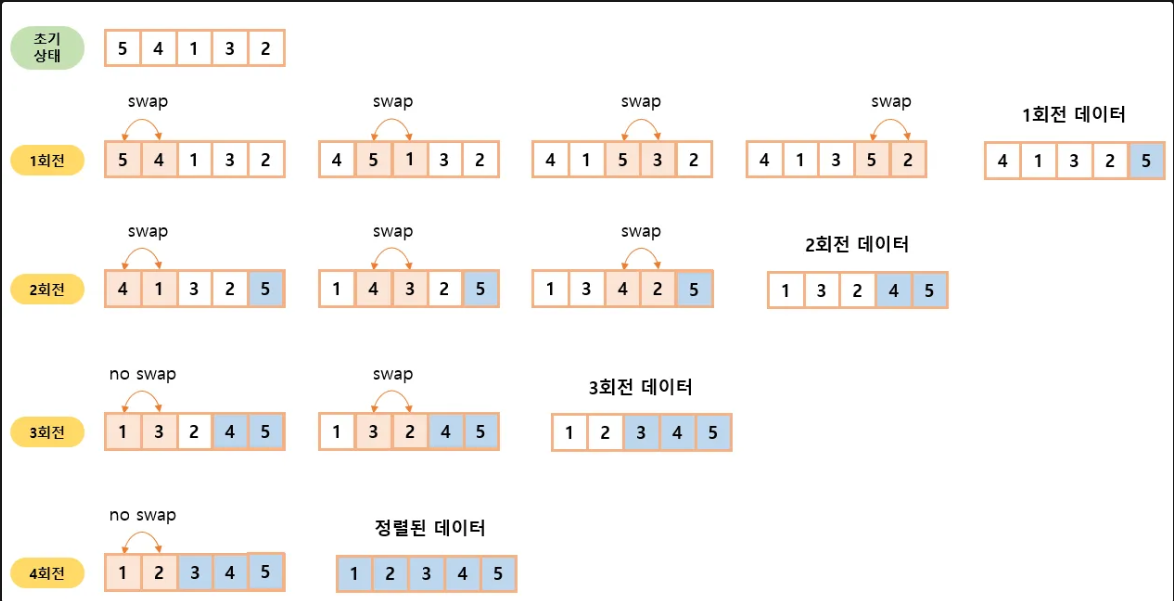
  • 인접한 데이터의 크기를 비교해 정렬

  • 시간복잡도 O(n2)O(n^2)

2) 대표코드(오름차순)

  • 루프를 돌면서 인접한 데이터간의 swap 연산으로 정렬
vector<int> bubble_sort(vector<int> target) {
	int n = target.size();
	int temp;
	for (int i = 0; i < n - 1; i++) {
		for (int j = 0; j < n - i - 1; j++) {
				if (target[j] > target[j + 1]) { //**swap**
				temp = target[j];
				target[j] = target[j + 1];
				target[j + 1] = temp;
			}
		}
	}
	return target;
}

int main(void) {
	int n = 5;
	vector<int> target = { 5, 3, 1, 4, 2 };
	auto result = bubble_sort(target);

	return 0;
}

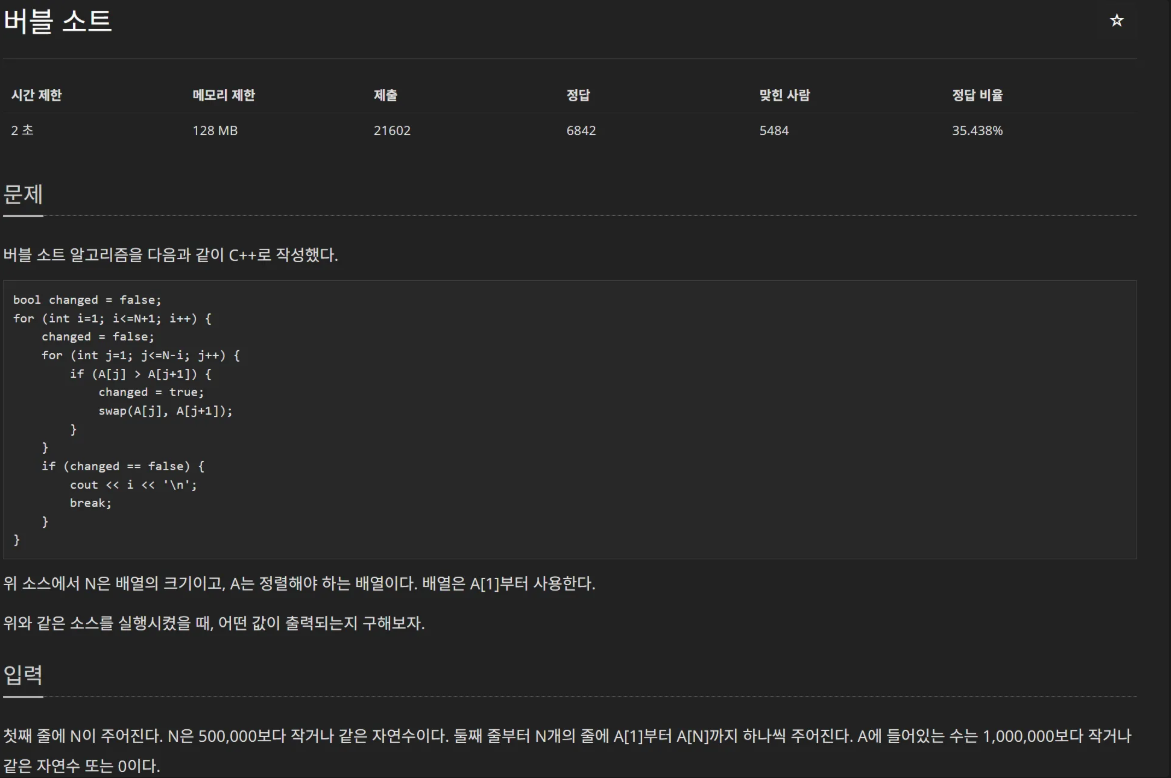
버블 소트 1377번

  1. 문제: 백준문제 바로 보러가기

  2. 코딩

  • vector <pair <int,int>> A(N)

    • 두 개의 값을 한 쌍으로 묶는 자료형

    • 이 경우, 두 개의 int형(정수형) 데이터를 하나로 묶어 저장

  • 문제의 요지: 초기배열에서 정렬완료배열까지 몇번의 버블정렬 검사가 이루어졌는가

    → 초기배열의 index값과 정렬후 배열의 index 값의 차이 중 max 값을 알면됨
    →그 max값의 +1 만큼 검사가 이루어짐

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);    
    cout.tie(NULL);
    
    int N;
    cin >> N;
    vector <pair<int,int>> A(N); //**
    
    for (int i = 0; i < N; i++) {
        cin >> A[i].first;
        A[i].second = i;
    }

    sort(A.begin(), A.end());

    int max = 0;
 	//핵심 코드
    for (int i = 0; i < N; i++) {
        if (max < A[i].second - i) {
            max = A[i].second - i;
        }
    }

    cout << max + 1;

	return 0;
}

2. 선택 정렬

1) 개념

  • 시간복잡도 O(n2)O(n^2)

2) 대표코드(오름차순)

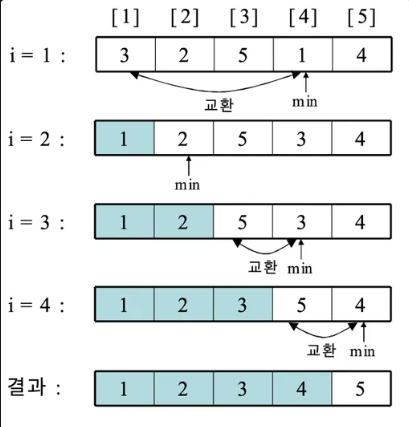
  • i=1 → 2번부터 끝까지 arr[1]보다 작은 min 값을 찾아 swap
  • i=2 → 3번부터 끝까지 arr[2]보다 작은 min 값을 찾아 swap
    ⇒ min값이 없음! 그냥 pass
  • 반복

for (int i = 0; i < size; i++) {
		int max_ind = i;
		for (int j = i + 1; j < size; j++) {
			if (N[max_ind] < N[j]) max_ind = j;
		}
		swap(N[i], N[max_ind]);
	}

소트인사이드 1427번

  1. 문제: 백준 바로 보러가기

  2. 코드

  • 문제의 요지: 선택정렬을 이용해서 내림차순 만들기
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {

	string N;
	cin >> N;
	int size = N.length();

	for (int i = 0; i < size; i++) {
		int max_ind = i;
		for (int j = i + 1; j < size; j++) {
			if (N[max_ind] < N[j]) max_ind = j;
		}
		swap(N[i], N[max_ind]);
	}

	for (int i = 0; i < size; i++) {
		cout << N[i];
	}

	return 0;
}

3. 삽입 정렬

1) 개념

  • 선택한 데이터를 적절한 위치에 삽입하는 것

2) 대표코드(오름차순)

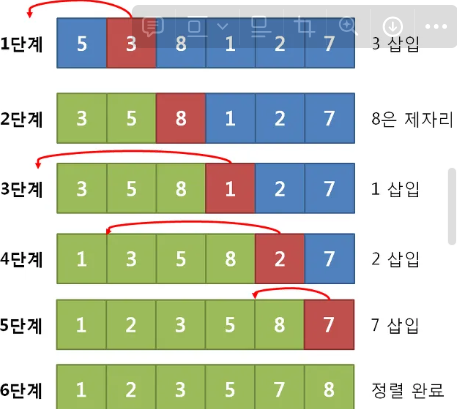
  • 2번째 원소부터 비교 시작한다

  • 이전 위치에 있는 원소들과 타겟이 되는 원소들을 비교한다(타켓 원소는 임시변수에 넣는다)

  • 타겟 원소가 이전 위치에 있던 원소보다 작다면 위치를 바꾼다

  • 이전 데이터도 차례대로 비교하며 정렬해나간다

  • 이 방법을 반복해서 정렬한다

//오름차순
int i, j, key, insert_ind;
	for (i = 1; i < N; i++) {
		key = A[i];
		for (j = i - 1; j >= 0; j--) {
			if (key < A[j]) {
				A[j+1] = A[j];
			}
			else {
				break;
			}
		}
		A[j+1] = key;	
	}

ATM 11399번

  1. 문제: 백준 문제 바로 보러가기

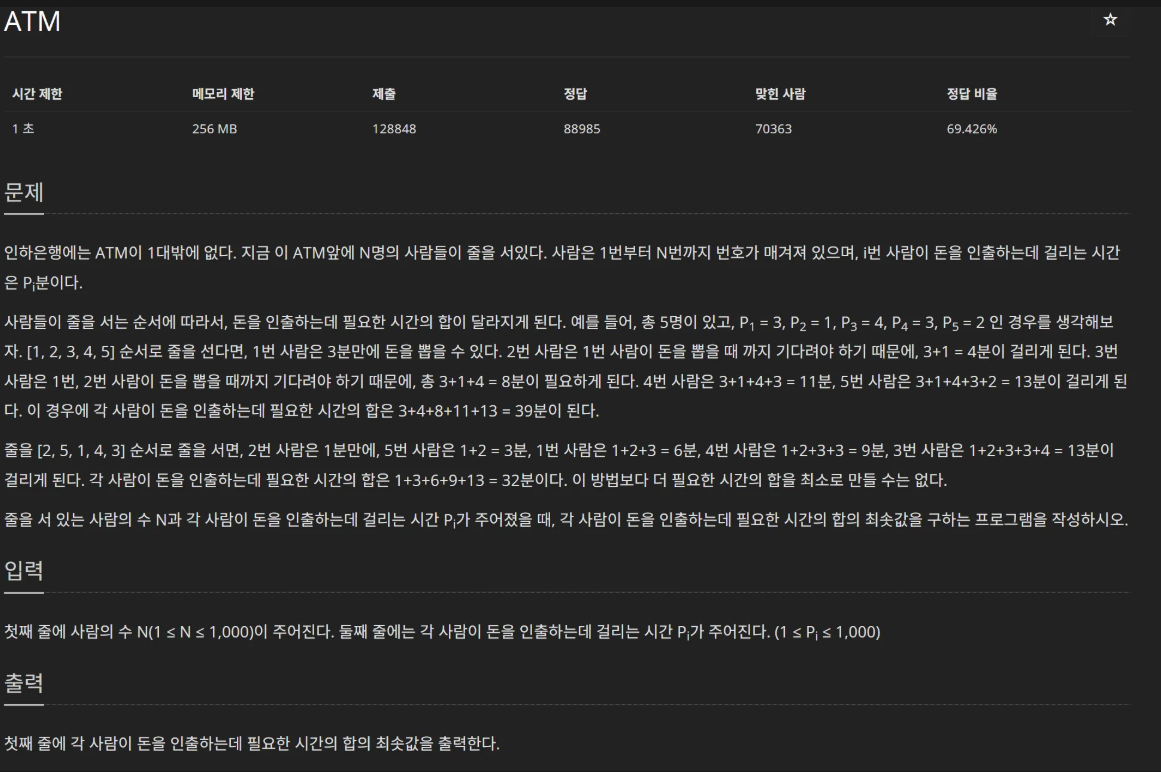
  1. 코드 → 삽입정렬로 오름차순 만들어보기
#include<iostream>
#include<vector> 
#include<algorithm>
using namespace std;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;
	vector <int>A(N, 0);
	vector <int>S(N, 0);

	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}

	//**삽입정렬** 
	int i, j, key, insert_ind;
	for (i = 1; i < N; i++) {
		key = A[i];
		for (j = i - 1; j >= 0; j--) {
			if (key < A[j]) {
				A[j+1] = A[j];
			}
			else {
				break;
			}
		}
		A[j+1] = key;	
	}

	S[0] = A[0];
	int sum = S[0];
	for (int i = 1; i < N; i++) {
		S[i] = S[i - 1] + A[i];
		sum += S[i];
	}
	cout << sum;
	

	return 0;
}

4. 퀵 정렬

1) 개념

  • 기준값pivot을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘
  • 시간복잡도: O(nlogn)O(nlogn) ~ O(n2)O(n^2)

2) 대표코드

  • 퀵정렬 수행방식(1) →평균 시간복잡도 O(nlogn)O(nlogn)
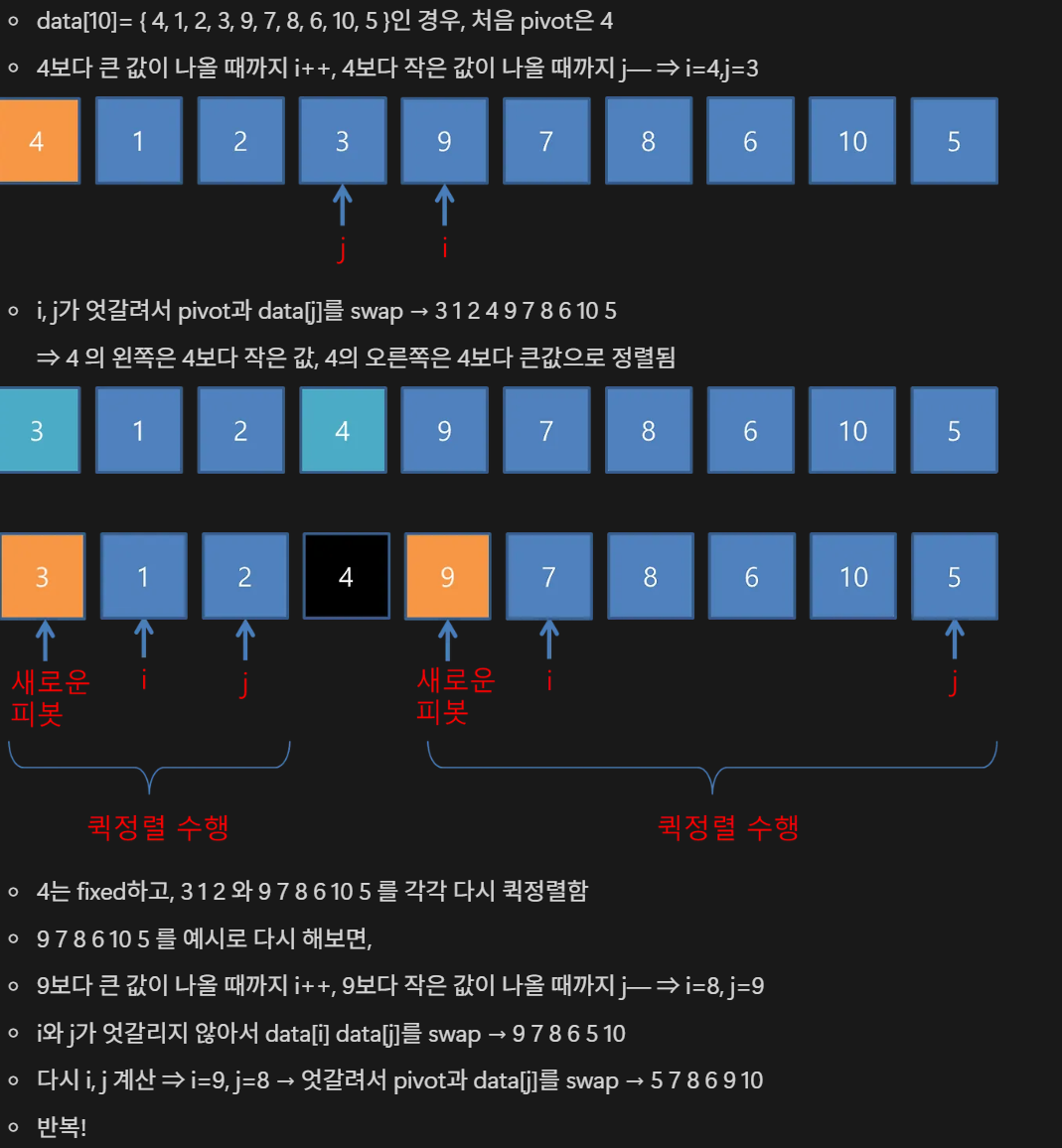
int data[10] = {4, 1, 2, 3, 9, 7, 8, 6, 10, 5};

void quick_sort(int *data, int start, int end){
    if(start >= end){
        // 원소가 1개인 경우
        return; 
    }
    
    int pivot = start;
    int i = pivot+ 1; // 왼쪽 출발 지점 
    int j = end; // 오른쪽 출발 지점
    int temp;
    
    while(i <= j){
        // 포인터가 엇갈릴때까지 반복
        while(i <= end && data[i] <= data[pivot]){
            i++;
        }
        while(j > start && data[j] >= data[pivot]){
            j--;
        }
        
        if(i > j){
            // 엇갈림
            temp = data[j];
            data[j] = data[pivot];
            data[pivot] = temp;
        }else{
            // i번째와 j번째를 스왑
            temp = data[i];
            data[i] = data[j];
            data[j] = temp;
        }
    } 
    
    // 분할 계산
    quick_sort(data, start, j - 1);
    quick_sort(data, j + 1, end);
}
 
int main(void){
    quick_sort(data, 0, 9);
    
    // 결과 확인
    for(int i=0; i<10; i++){
        printf("%d ", data[i]);
    }
    return 0;
}
  • 퀵정렬 수행방식(2) ⇒ 평균 시간복잡도 O(n)O(n)
    ⇒ 밑의 문제의 코드!

K번째 수

  1. 문제: 백준 문제 바로 보러가기

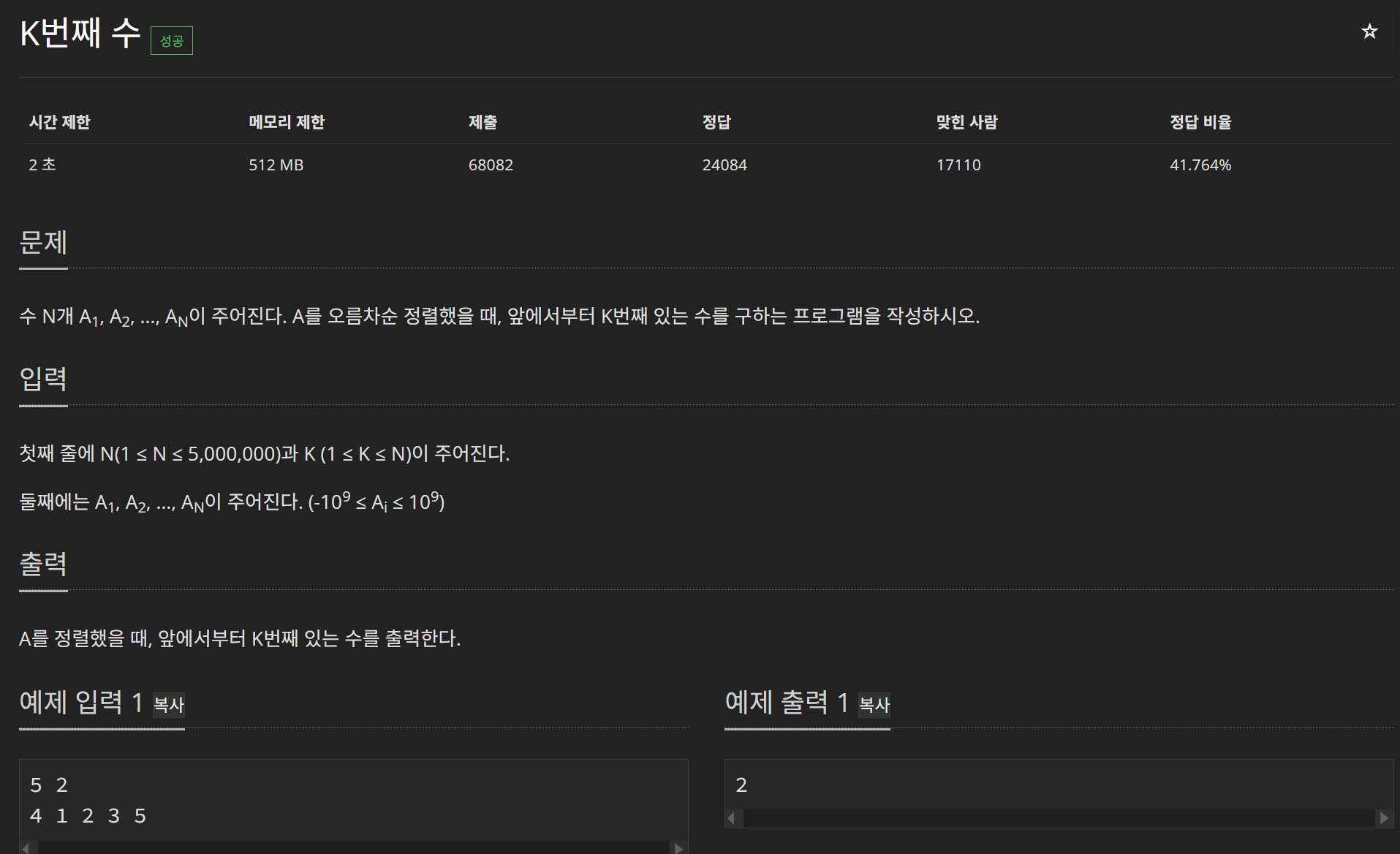
  1. 코드

  • 중앙값을 pivot으로 하고 1차 퀵정렬 진행 후 j 위치 반환

  • K < j ⇒ 왼쪽 부분만 퀵정렬 진행
    K > j ⇒ 오른쪽 부분만 퀵정렬 진행
    K=j ⇒ 퀵정렬 stop

  • 위의 개념설명때의 코드처럼 모든 부분을 다 퀵정렬하지 않고, K번째 필요한 부분만 퀵정렬 하기 때문에 시간복잡도가 O(n)O(n)으로 줄어듦!

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

void quickSort(vector <int>& A, int S, int E, int K);
int partition(vector <int>& A, int S, int E);
void swap(vector <int>& A, int i, int j);

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N, K;
	cin >> N >> K;
	vector <int> A(N, 0);

	for (int i = 0; i < N; i++) {
		cin >> A[i];
	}

	quickSort(A, 0, N-1, K-1);

	cout << A[K-1];

	return 0;
}

void quickSort(vector <int>& A, int S, int E, int K) {
	int pivot = partition(A, S, E);
	if (pivot == K) { //pivot이 K번재 수라면 더는 구할 필요가 없음
		return ;
	}
	else if (K < pivot) { // 왼쪽 그룹만 정렬 수행
		quickSort(A, S, pivot - 1, K);
	} 
	else  { // K > pivot -> 오른쪽 그룹만 정렬 수행
		quickSort(A, pivot + 1, E, K);
	}
}

int partition(vector <int>& A, int S, int E) {
	if (S + 1 == E) { //2개의 요소만 있는 경우
		if (A[S] > A[E]) {
			swap(A, S, E);
		}
		return E;
	}

	int M = (S + E) / 2; // 중앙값을 피벗으로 설정
	swap(A, S, M); //중앙값을 첫번째 요소로 이동

	int pivot = A[S];
	int i = S + 1;
	int j = E;
	while (i <= j) {
		while (pivot < A[j] && j>0) {
			j--;
		}
		while (pivot > A[i] && i <= A.size() - 1) {
			i++;
		}
		if (i <= j) {
			swap(A, i++, j--);
		}
	}

	A[S] = A[j];
	A[j] = pivot;
	return j;   // 피벗 위치 반환

}

void swap(vector <int>& A, int i, int j) {
	int temp = A[i];
	A[i] = A[j];
	A[j] = temp;
}

5. 병합 정렬

1) 개념

  • 데이터를 분할하고 분할할 집합을 정렬하며 합치는 알고리즘

  • 시간복잡도 : O(nlogn)O(nlogn)

  • 2개의 그룹을 병합하는 과정
    - 투포인터 개념을 이용해 왼쪽 오른쪽 그룹을 병합
    - 오른쪽 포인터의 값을 비교해 작은 값을 결과 배열에 추가, 포인터를 오른쪽으로 1칸 이동

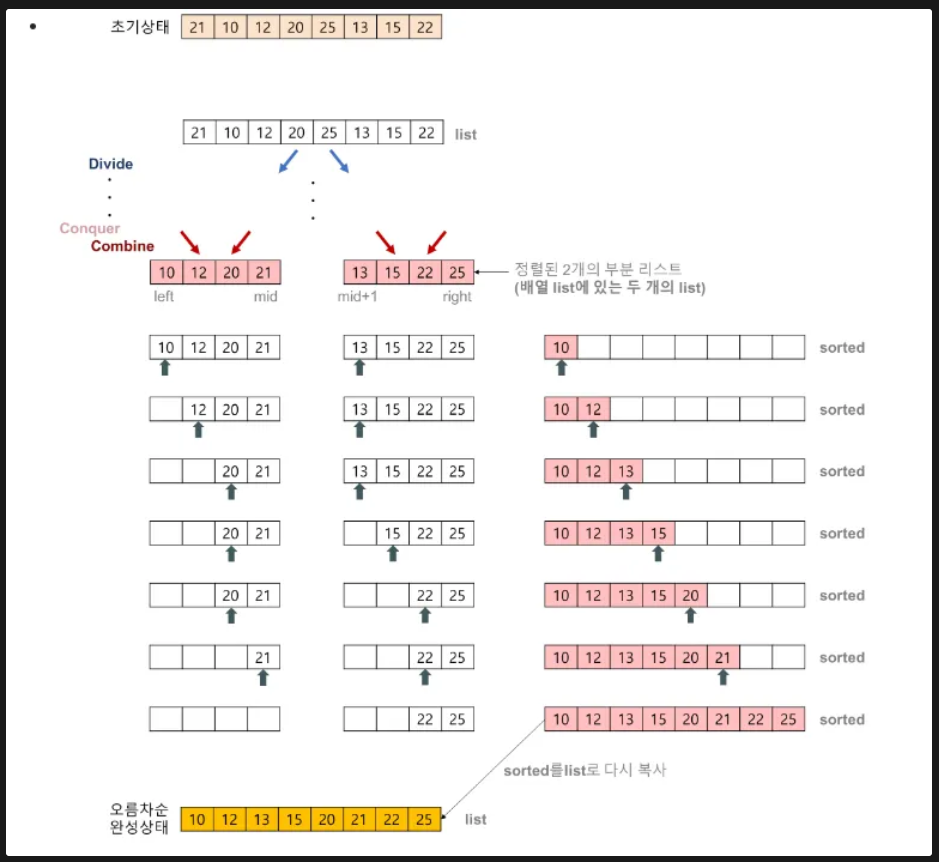
2) 대표 코드

  1. conquer와 merge를 분리해서 코드 작성
int arr[100];
int sorted[100];
//병합 merge
void merge(int start, int end){
    int mid = (start + end) / 2;
    int i = start, j = mid+1, k = start;
    while (i <= mid && j <= end) {
        if (arr[i] <= arr[j]) 
            sorted[k++] = arr[i++];
        else
            sorted[k++] = arr[j++];
    }
    while (i <= mid)
        sorted[k++] = arr[i++];
    while (j <= end)
        sorted[k++] = arr[j++];
        
 	// 병합된 결과를 다시 arr에 반영
	//다시 반영되지 않으면 arr에 데이터들이 남아 메모리를 불필요하게 차지하게 됨
	//-> 오류를 발생시킬 수도 있음
    for (int i = start; i <= end; i++) {
        arr[i] = sorted[i];
    }
}

//분리 conquer
void merge_sort(int start, int end) {
    if (start < end) {
        int mid = (start + end) / 2;
        merge_sort(start, mid);
        merge_sort(mid + 1, end);
        merge(start, end);
    }
}
  1. conquer와 merge를 하나의 함수로 통합해서 작성
void merge_sort(int s, int e) {
	if (e - s < 1) {
		return;
	}

	int m = (e + s) / 2;
	//conquer!!
	merge_sort(s, m);
	merge_sort(m + 1, e);

	//temp에 arr을 다 복사하고, 최종결과를 arr에 저장하는 방법
	for (int i = s; i <= e; i++) {
		temp[i] = arr[i];
	}

	int k = s;
	int ind1 = s;
	int ind2 = m + 1;

	while (ind1 <= m && ind2 <= e) {
		if (temp[ind1] < temp[ind2]) {
			arr[k++] = temp[ind1++];
		}
		else {
			arr[k++] = temp[ind2++];
		}
	}

	while (ind1 <= m) {
		arr[k++] = temp[ind1++];
	}
	while (ind2 <= e) {
		arr[k++] = temp[ind2++];
	}
}

수 정렬하기2 2751번

  1. 문제: 백분 문제 바로 보러가기
  1. 코드
  • sort(A.begin(), A.end())를 써도 되지만, 주제에 맞게 병합정렬을 사용해보자!!
#include<iostream>
#include<vector>
using namespace std;
void merge(int s ,int e);
void conquer(int s, int e);
vector<int>arr;
vector<int>sorted;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int N;
	cin >> N;

	//메모리 할당
	arr.resize(N);
	sorted.resize(N);

	for (int i = 0; i <N; i++) {
		cin >> arr[i];
	}

	conquer(0, N-1);

	for (int i = 0; i <  N; i++) {
		cout << arr[i] << "\n";
	}
	return 0;
}
void merge(int s, int e) {
	int m = (s + e) / 2;
	int ind1 = s;
	int ind2 = m + 1;
	int k = s;

	while (ind1 <= m && ind2 <= e) {
		if (arr[ind1] < arr[ind2]) {
			sorted[k++] = arr[ind1++];
		}
		else {
			sorted[k++] = arr[ind2++];
		}
	}
	while (ind1 <= m) {
		sorted[k++] = arr[ind1++];
	}
	while (ind2 <= e) {
		sorted[k++] = arr[ind2++];
	}
	
	for (int i = s; i <= e; i++) {
		arr[i] = sorted[i];
	}
}
void conquer(int s, int e) {
	if (s < e) {
		int m = (s + e) / 2;
		conquer(s, m);
		conquer(m + 1, e);
		merge(s, e);
	}
}

버블 소트 1517번

  1. 문제: 백준문제 바로 보러가기

  2. 코드

  • 예시: 3 2 8 1 7 4 5 6
  • (32)(81) → 첫번째 merge에서 2와 1이 앞으로 1칸씩 이동
  • (2318) → 두번째 merge에서 1이 2칸 앞으로 이동
  • (1238)(4567) → 마지막 merge에서 4 5 6 7이 1칸씩 앞으로 이동

⇒ arr[ind1] > arr[ind2] 일때, cnt가 ind2-k만큼 증가!!

#include<iostream>
#include<vector>
using namespace std;
void merge(int s, int e);
void conquer(int s, int e);
vector <int> arr;
vector <int> sorted;
int cnt=0;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;
	 
	arr.resize(n);
	sorted.resize(n);

	for (int i = 0; i < n; i++) {
		cin >> arr[i];
	}

	conquer(0, n - 1);

	cout << cnt ;

	return 0;
}
void merge(int s, int e) {
	int m = (s + e) / 2;
	int ind1 = s;
	int ind2 = m + 1;
	int k = s;

	while (ind1 <= m && ind2 <= e) {
		if (arr[ind1] <= arr[ind2]) {
			sorted[k++] = arr[ind1++];
		}
		else {
			sorted[k++] = arr[ind2++];
			cnt += ind2-k;  //핵심 코드!!        
		}
	}

	while (ind1 <= m) {
		sorted[k++] = arr[ind1++]; 
	}

	while (ind2 <= e) {
		sorted[k++] = arr[ind2++]; 
	}

	for (int i = s; i <=e; i++) {
		arr[i] = sorted[i];
	}
}
void conquer(int s, int e) {
	if (s < e) {
		int m = (s + e) / 2;
		conquer(s, m);
		conquer(m + 1, e);
		merge(s, e);
	}
}

6. 기수 정렬

1) 개념

  • 값을 비교하지 않는 특이한 정렬

  • 값을 놓고 비교할 자릿수를 정한 다음 해당 자릿수만 비교

  • 시간복잡도: O(kn)O(kn) k=데이터의 자릿수

2) 대표코드

	for (int i = 0; i < n; i++) { 
		cin >> number; 
		count[number]++;
	}

	for (int i = 0; i <=10000; i++) {
		if (count[i] > 0) {
			for (int j = 0; j < count[i]; j++) {
				cout << i << "\n";
			}
		}
	}

수 정렬하기3 10989번

  1. 문제 → 오름차순하기: 백준 문제 보러가기

  2. 코드

#include<iostream>
#include<vector>
using namespace std;
int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;

	int number=0;
	int count[10001] = { 0 };

	for (int i = 0; i < n; i++) { 
		cin >> number; 
		count[number]++;
	}

	for (int i = 0; i <=10000; i++) {
		if (count[i] > 0) {
			for (int j = 0; j < count[i]; j++) {
				cout << i << "\n";
			}
		}
	}

	return 0;

}
profile
jade
이전 포스트

Chap3 자료구조

다음 포스트

Chap5-1)탐색

0개의 댓글