
Networks
Network: graph representation with data
- 네트워크는 서로 상호작용하는 entity 간 복잡한 시스템을 설명할 수 있는 범용 언어임
- 표현하고자 하는 object를 선으로 연결함으로써 network를 만듦
- 데이터 가용성을 고려하였을 때 다양한 도메인에서 사용될 수 있음
- web/mobile, bio, health, medical, etc.
- Impact!
- social network, drug design, AI reasoning
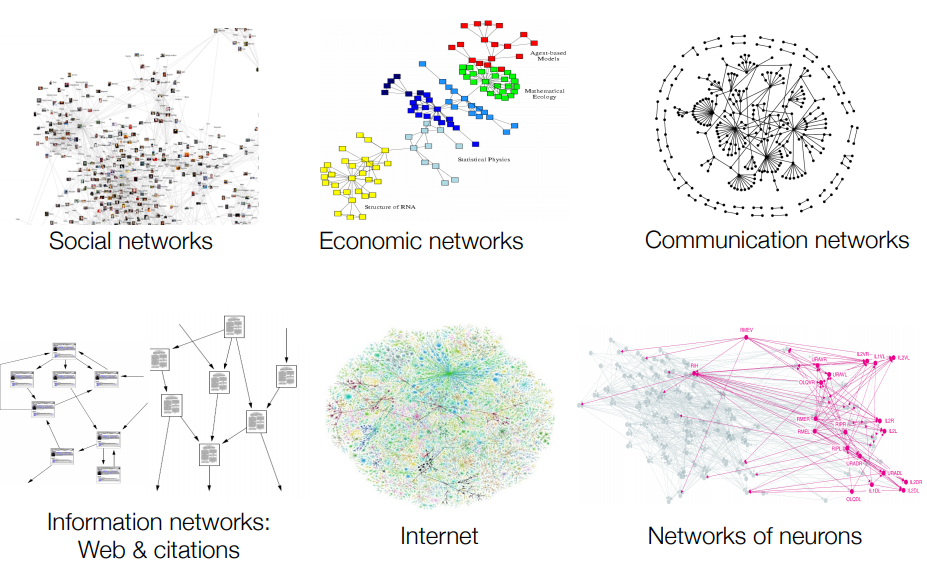
Many types of networks
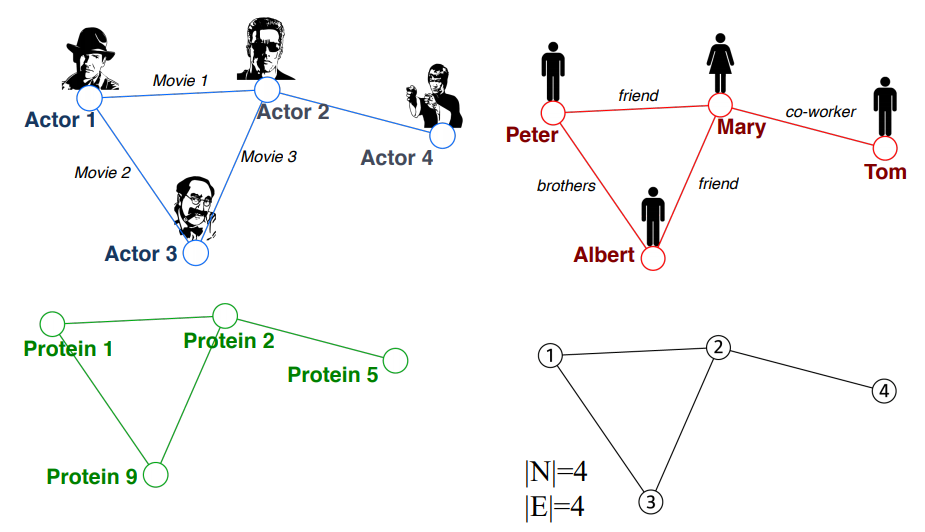
- 모든 network는 저마다 object가 의미하는 바가 다르며, 그들간의 관계 또한 다름
- 주어진 network를 이해하지 못하면 모델링을 할 수 없음! (투빅스1강이 EDA인 이유)
Ways to Analyze Networks
- Node classification
- Link prediction
- Community detection
- Netwrok similarity
Structure of Graphs
Components of a Network
- Objects N: nodes, vertices
- Interactiosn E: links, edges
- System G(N, E): network, graph
Networks or Graphs?
- Network: real system
- web, social network
- Language: network, node, drug network
- Graph: netwowrk의 수학적 표현
- web graph, social graph
- Language: graph, vertex, edge
- 서로 경계가 모호하기때문에 일반적으로 혼용하는 편!
Choice of Network Representation
Direction of edges
- Undiredcted graph: 링크가 양방향인 그래프
- EX) collaborations, friendship
- Directed graph: 링크에 특정 방향이 주어지는 그래프
- citation/quotation, 인스타 DM, 팔로잉, 좋아요
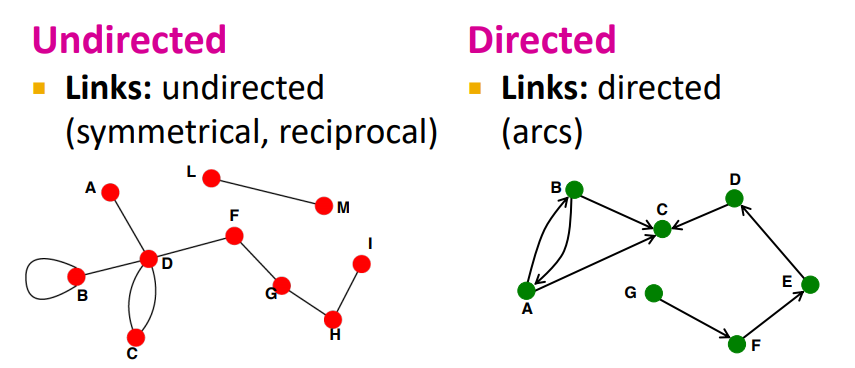
- citation/quotation, 인스타 DM, 팔로잉, 좋아요
Node Degrees
- Degree(차수): 노드에 부속되어 있는 link의 수
- Undirected graoph의 평균 차수
(=edge 개수, =node 개수, =i째 node의 차수)
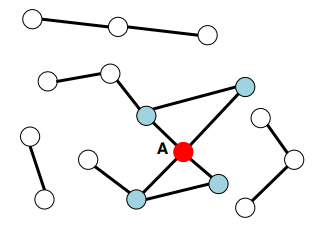
- 위의 예시에서는
- Directed의 경우는 in-degree와 out-degree가 구분됨
- 전체 차수는 두 가지 degree 총합임
- 전체 차수는 두 가지 degree 총합임
Complete Graph
- undirected graph의 최대 edge 개수
- Complete graph: 최대 edge개수를 가진 undirected grpah
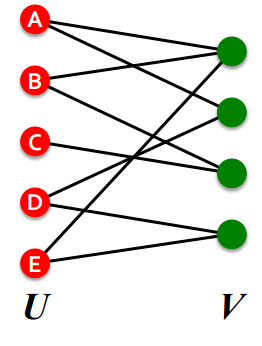
Bipartite Graph
- Bipartite graph: 서로 다른 종류의 독립된 노드들로 구성된 그래프
- 두 가지 노드 타입 U, V로 나눌 수 있음
- U에 속하는 노드는 V에 속한 노드에게만 연결되고 U끼리는 독립임
- V에 속하는 노드는 U에 속한 노드에게만 연결되고 V끼리는 독립임
- Bipartite graph는 실제 도메인에서 많이 나타나는 구조이며, 특히 추천시스템에서 많이 사용되는 개념임
Representing Graphs
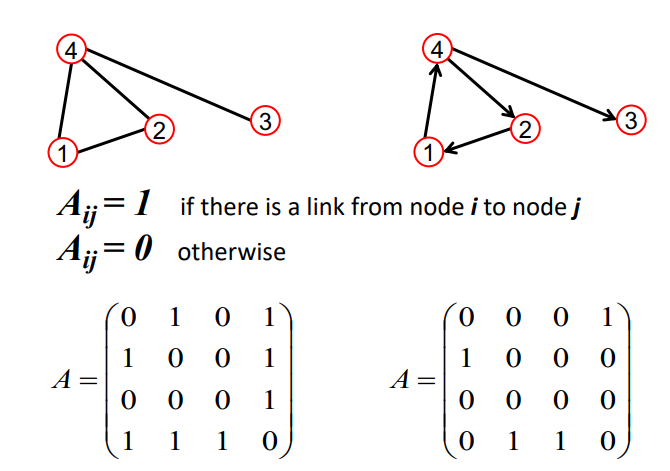
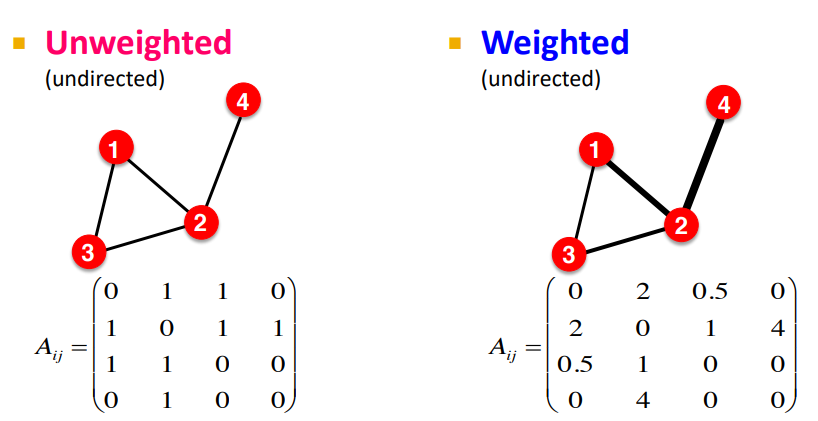
Adjacency Matrix
- Adjacency Matrix(인접행렬): 그래프를 연결 유무를 1과 0으로 나눠 행렬로 표현한 것
- Undirected의 경우 대칭으로 나타나며 Undirected는 단방향일 수 있기 때문에 대칭이 아닐 수도 있음
- 노드가 많아질 수록 즉, 행렬의 차원이 커질 수록 Sparse해진다는 단점이 있음
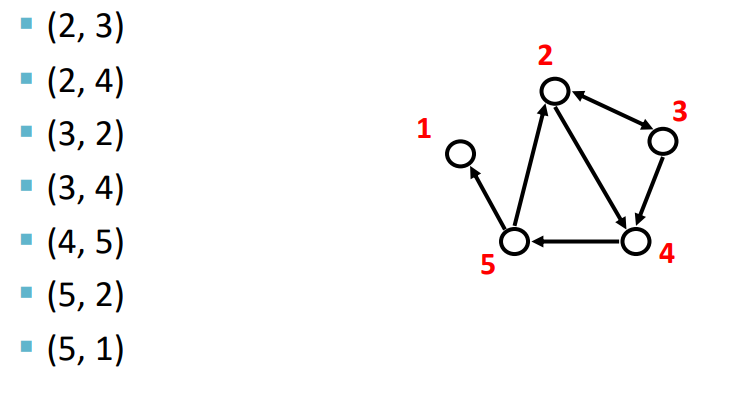
Edge list
- Edge를 연결된 노드 쌍으로 표현한 것
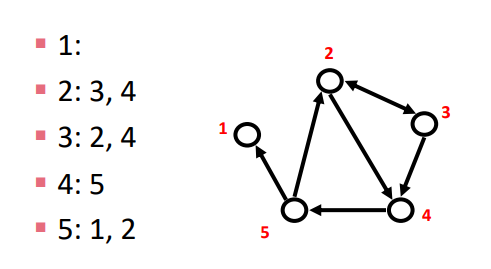
Adjacency list
- 출발방향의 노드를 Key값으로, 도착 노드를 Value값으로 가지는 Dictioanry형태
- 단방향이거나 거대한 그래프에서 효율이 좋음
Edge Attrbutes
- Weight: edge에 weight를 줄 수 있음 (와인 추천 시 와인에 대한 평점을 edge에 weight 주기)
- Ranking: 짱절친, 절친, 아는 사이
- Type: 친구, 친척, 직장동료
More types of Graph
Connectivity of Undirected Graphs
- Connected graph(undirected): 어떤 노드에서 출발하든지 다른 모든 노드로 도착할 수 있음
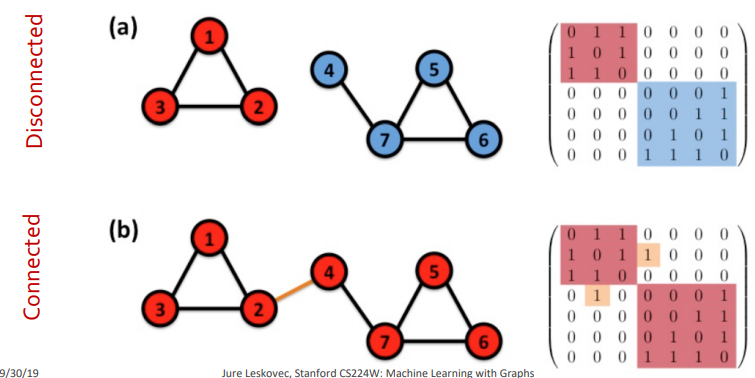
- Disconnected graph: 최소 2개 이상의 connected graph로 구성됨
- Bridge edge: 삭제되면 connected에서 disconnected로 바꿀 수 있는 edge
- Articulation node: 삭제되면 connected에서 disconnected로 바꿀 수 있는 node
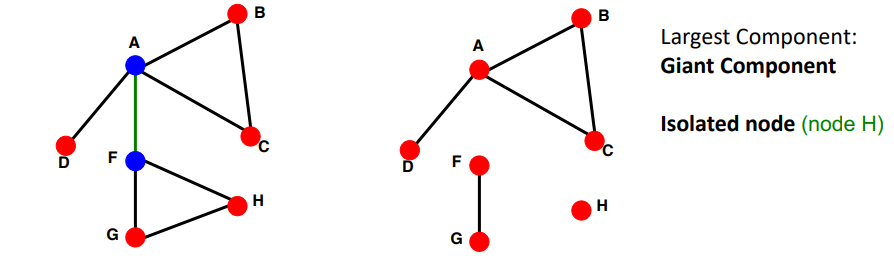
- Disconnected의 경우 인접행렬은 block-diagonal 형태가 된다
Connectivity of Directed Graphs
-
Strongly connected directed graph: 어떤 노드에서 출발하든지 edge방향을 지키면서 다른 모든 노드로 도착할 수 있음
-
Wealky connected directed graph: 어떤 노드에서 출발하든지 edge방향을 무시한다면 다른 모든 노드로 도착할 수 있음
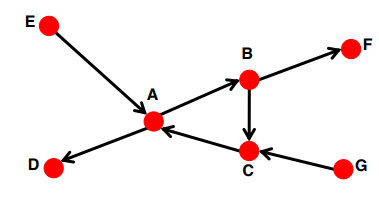
-
Strongly connected components(SCCs): 그래프에서 부분적으로 나타나는 connected subgraph
- SCCs 포함유무에 따라 In-component, Out-component로 분류
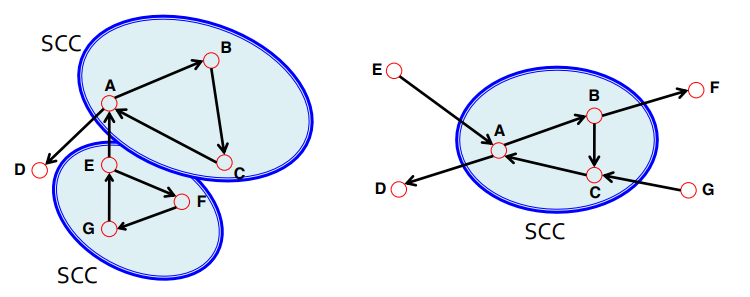
- SCCs 포함유무에 따라 In-component, Out-component로 분류
5개의 댓글
Network
- 서로 상호작용하는 entity 간 복잡한 시스템을 설명할 수 있는 범용 언어
- 구성요소 : Objects (N, nodes) + Interactions (E, edges) + System (G(N,E))
Network Representation
- Undirected : 그래프 양방향 / Directed : 특정 방향이 주어지는 그래프
- Degree : 노드에 연결되는 link 수
- Complete Graph : 모든 노드에 모두 연결된 그래프 (N(N-1)/2)
- Bipartite Graph : 서로 다른 종류의 독립된 노드들로 구성된 그래프
Representing Graph
- Adjacency Graph (인접행렬) : 그래프 사이의 연결 관계 표현
- Unweighted / Weighted : edge 굵기가 달라짐
- Strongly Connected (방향 지키면서) / Weakly Connected (방향 무시하면) → 다른 노드로 도착 가능
자세한 건 리뷰에 남겼어용
좋은 강의 감사합니당 ~
1개의 답글
기본적인 그래프 관련 용어와 구조에 대해 알 수 있었습니다.
Structure of Graphs
- Objects N: nodes, vertices
- Interactions E: links, edges
- System G(N, E): network, graph
Network Representation
- Undiredcted graph: 링크가 양방향인 그래프
- Directed graph: 링크에 특정 방향이 주어지는 그래프
- Degree(차수): 노드에 부속되어 있는 link의 수
- Complete graph: 최대 edge개수를 가진 undirected grpah
- Bipartite graph: 서로 다른 종류의 독립된 노드들로 구성된 그래프
Representing Graph
- Adjacency Matrix(인접행렬): 그래프를 연결 유무를 1과 0으로 나눠 행렬로 표현한 것
- Edge list: Edge를 연결된 노드 쌍으로 표현한 것
Connectivity of Directed Graphs
- Strongly connected directed graph: 어떤 노드에서 출발하든지 edge방향을 지키면서 다른 모든 노드로 도착할 수 있음
- Wealky connected directed graph: 어떤 노드에서 출발하든지 edge방향을 무시한다면 다른 모든 노드로 도착할 수 있음
그래프의 기초를 다질 수있는 좋은 강의였습니다.
답글 달기
이번 강의는 신윤종님께서 진행해주셨습니다.
Network란 data들간의 관계, graph representation을 일반적으로 이루는 말입니다.
System G(network,graph)은 object N(node, vertices)와 object사이의 interation E(link, edge)으로 이루어져있습니다. graph에서는 node간의 edge의 수를 degree라고 합니다.
Graph 종류
- edge의 방향이 없는 그래프를 undirected graph, 링크의 방향이 있는 그래프를 directed graph라고 합니다.
- Complete graph : undirected graph에서 모든 node가 이어진 graph
- Bipartite graph : node의 종류를 독립적으로 분리할 수 있는 graph
Representing Graph
- Adjacency Matrix(인접행렬) : node간의 연결관계를 행렬로 표현
- Edge list : 연결 node를 쌍으로 표현. directed의 표현에서는 (2,4)=!(4,2)
- Adjacency list : (in directed) 출발 node를 key, 도착 node를 value값으로 갖는 dictionary
- Edge attribute : Weight, Ranking, Type,
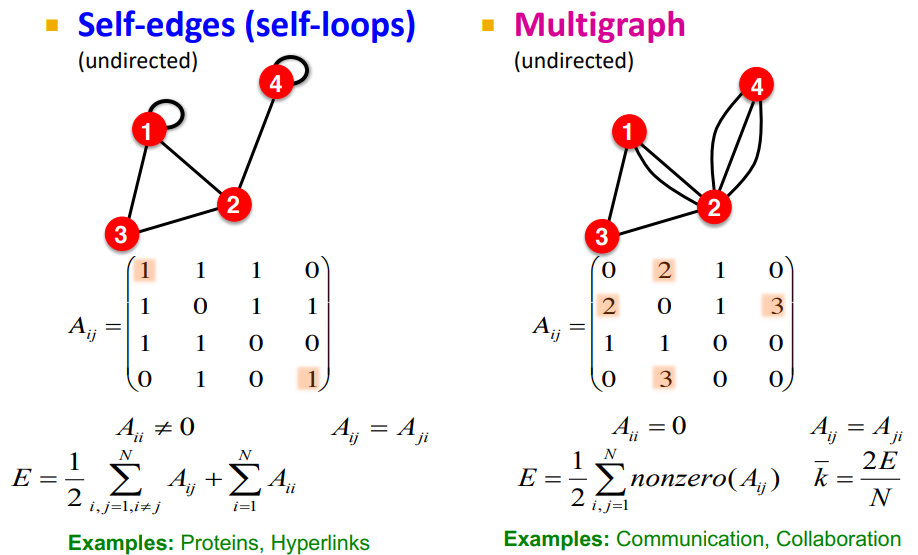
- node와 edge는 self-loop나, 두 node사이의 여러개의 edge를 갖는 multi graph도 가능하다
Undireced Graph의 특성
- Connected graph란, 어떤 노드에서 출발하든지 다른 모든 노드로 도착할 수 있는 graph를 말하고, isolated node가 없다는 의미다. <-> Disconnected graph :최소 2개 이상의 connected graph로 구성. 이 때 adgacency list는 block-diagonal형태 이다.
- Bridge edge : 삭제되면 connected -> disconnected 되는 edge
- Articulation node : 삭제되면 connected -> disconnected 되는 node
Direced Graph의 특성
- strong connected directed graph : 어떤 노드에서 출발하던 connected <-> weakly connected directed graph :방향무시하면 connected graph
- Strongly connected components(SCCs) : connected supgraph
graph의 기본적인 용어를 정리할 수 있는 유의미한 시간이었습니다. 감사합니다.
답글 달기




투빅스 13기 정민준
그래프의 구조와 속성에 대해 전반적으로 알 수 있었습니다.
좋은강의 감사합니다 :)