2. Properties of Networks and Random Graph Models

tobigsGNN·2021년 2월 10일
CS224WGNNgraph studymachine learning with graphnetworkproperties of networksrandom graph model
6

CS224W Review

목록 보기
2/18
post-thumbnail

작성자 : 이예진

Contents

  1. Intro
  2. Network Properties: How to Measure a Network
  3. Real-World Networks (MSN Messenger)
  4. Erdos-Renyi Random Graph Model
  5. The Small-World Model
  6. Kronecker Graph Model
  7. Summary

Properties of Networks and Random Graph Models

0. Intro

이 장에서는 기본적인 Network의 속성과 Random Graph Model 들에 대해서 배웁니다. 기본 속성의 개념과 용어를 숙지하는 위주로 리뷰하겠습니다.

Keyword
degree distribution,path length,clustering coefficient, connected components,random graph model, small-world, kronecker graph

1. Network Properties: How to Measure a Network

Network 속성들, 즉 어떻게 Network를 정량적으로 측정하는지 알아보겠습니다.
크게 4가지 방법이 있습니다.

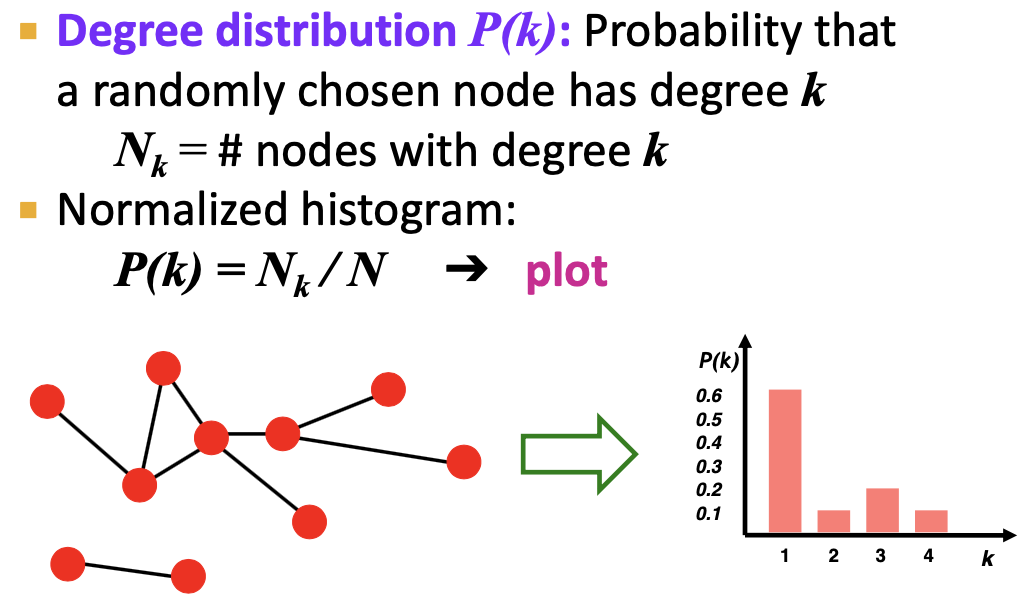
(1). Degree distribution : P(k)

degree distribution (차수 분포) 입니다. node에 연결 된 엣지의 갯수가 degree k 라고 할 때, 무작위로 선택한 node 가 k개의 차수를 가지고 있는 확률을 P(k) 라고 합니다.
N_k 는 degree 가 k 인 노드의 수 이고, 이를 Normalize 해서 P(k)를 구합니다. histogram 으로 나타내면 다음과 같습니다.

(2). Paths in a Graph - 경로

Path : 각 노드가 다른 노드와 연결된 연속성을 경로라고 합니다.

Distance(거리) : 연결된 node들의 가장 짧은 경로 입니다.
directed graphs 에서는 방향을 고려합니다.
Network Diameter(직경) : 그래프에서 노드 간의 최대거리입니다. 어떤 그래프에서 Path의 최대값. 가장 먼 두 node의 거리를 나타내주는 값이라고 생각하면 됩니다.
Average path length : directed graph에서 평균 경로 길이를 나타낼 수 있습니다.

(3). Clustering Coefficient - 결집계수

Clustering Coefficient 는 undirected graphs 에서 사용됩니다.
페이스북 소셜 네트워크 같은 곳에서 사용할 수 있습니다.

핵심 아이디어는 노드 i 의 이웃들은 서로 얼마나 연결되어 있을까? 입니다.

Clustering Coefficient 는 C 로 나타내고 0~1 사이 값을 가집니다.
노드 i 에 대한 C를 구하는 공식은 다음과 같습니다.

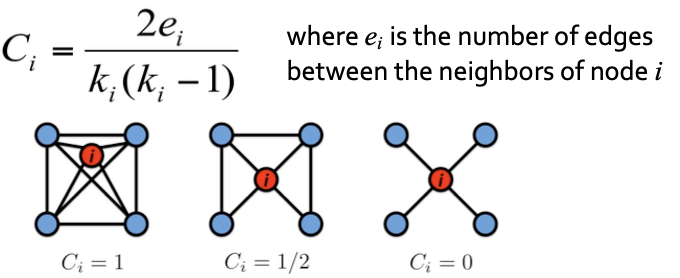
노드 i 의 이웃이 실제로 연결된 엣지 갯수 (e_i) 를 이웃 차수로 가질 수 있는 경우의 수 (k_i)(k_i -1)로 나눠줍니다.
-> 두번째 경우, i 의 이웃은 4개의 노드가 있습니다. 이 이웃들이 실제로는 3개의 연결된 엣지를 가지고 있기 때문에 분모는 2x3 이고, 분모는 경우의 수 4x3이 됩니다.

Average clustering coefficient : 평균 결집계수는 각 노드의 C를 구한 값을 평균내서 구할 수 있습니다.

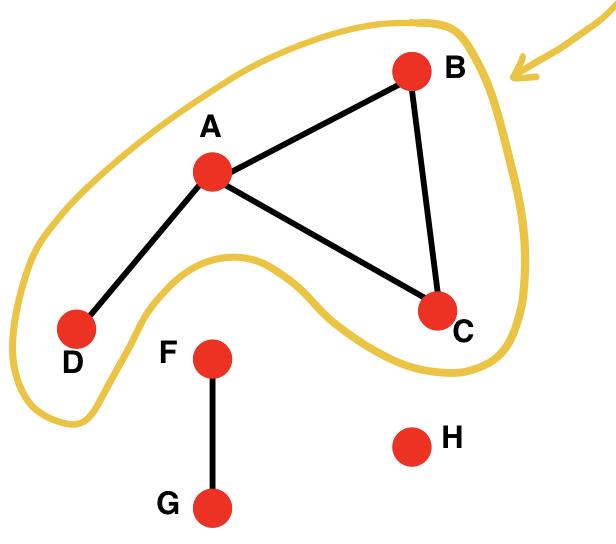
(4). Connectivity - 연결성

연결된 구성요소 중에 가장 큰 크기 입니다. BFS(너비우선탐색) 알고리즘으로 찾습니다.
Lagest component = Giant component
(뒤에서는 GCC라고 언급하기도 합니다.)

2. Real-World Networks (MSN Messenger)

이 네 가지 네트워크 속성이 Real-World Networks 에서는 어떻게 측정되는지 MSN Messenger 예시를 보도록 하겠습니다.

1. Degree Distribution


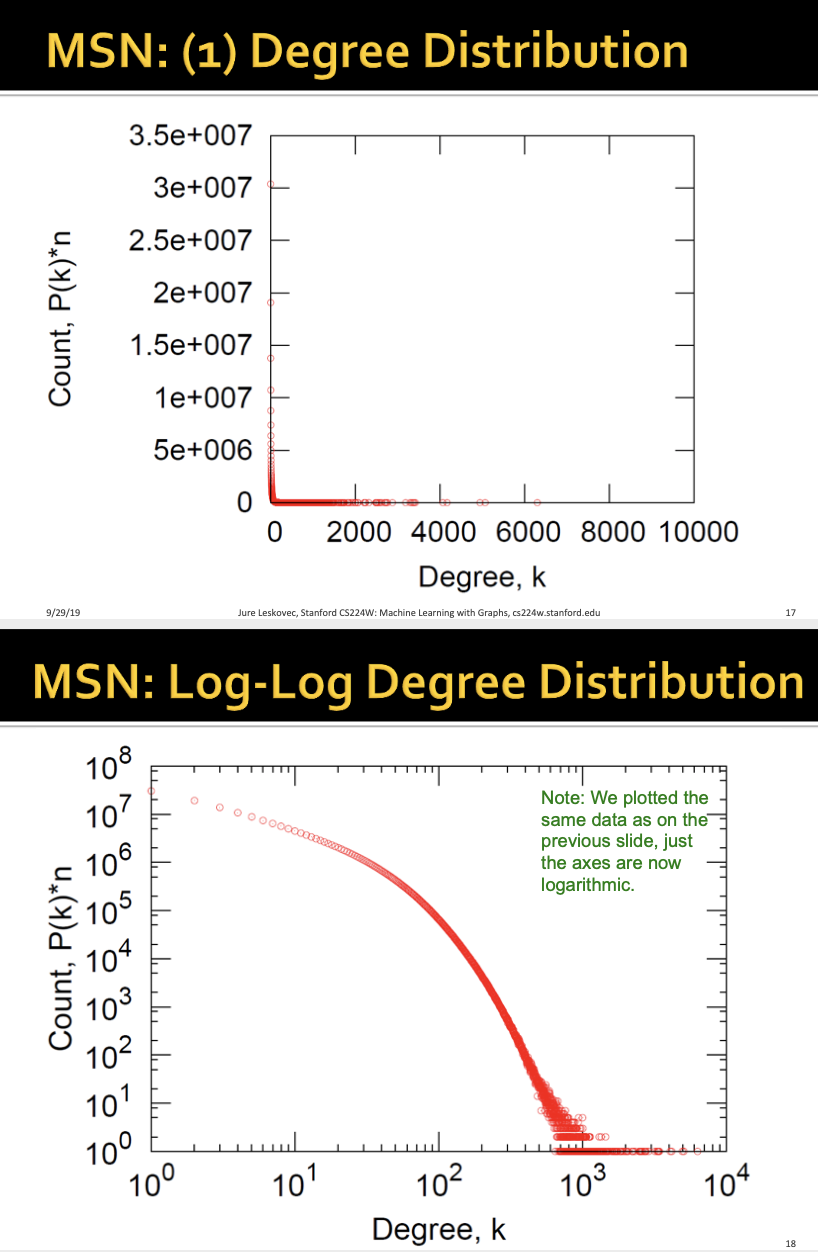
정의대로 분포를 시각화하면 분포가 잘 보이지 않아서 로그 스케일링한 log-log degree distribution을 보겠습니다. 대부분의 사람들이 10^3 정도에 몰려서 분포해 있고, 몇몇의 사람들이 더 높은 연결 수(degree k)를 가지고 있습니다.

2. Clustering

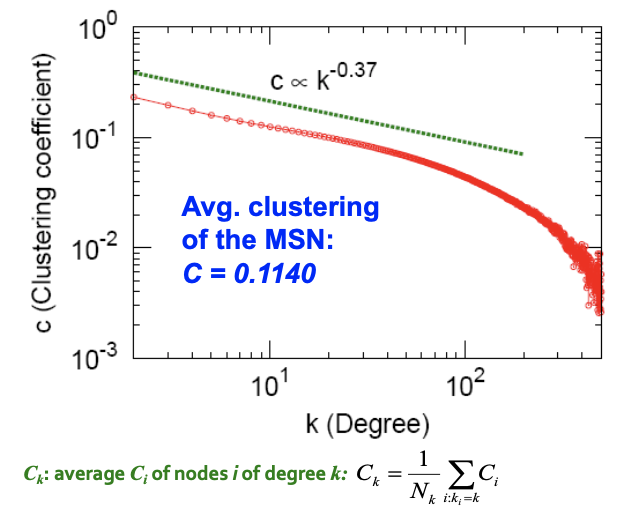
  • 평균 결집 정도는 0.1140 입니다. 크다, 작다 판단 보다는 그냥 숫자로 이해해야합니다.
  • C와 K간의 기울기를 보면 반비례함을 알 수 있습니다. degree 가 높은 node 일 수록, 이웃들 간의 연결(결집계수 C) 는 작아진다는 것을 의미합니다.

3. Connected Components


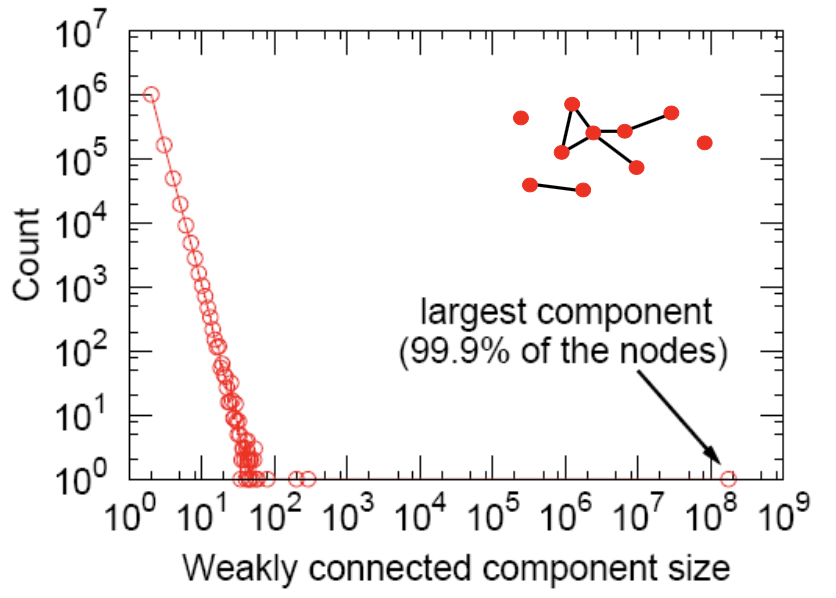
largest component(giant component)는 99.9% 의 노드들을 가진 큰 component임을 알 수 있습니다.

4. Diameter of WCC

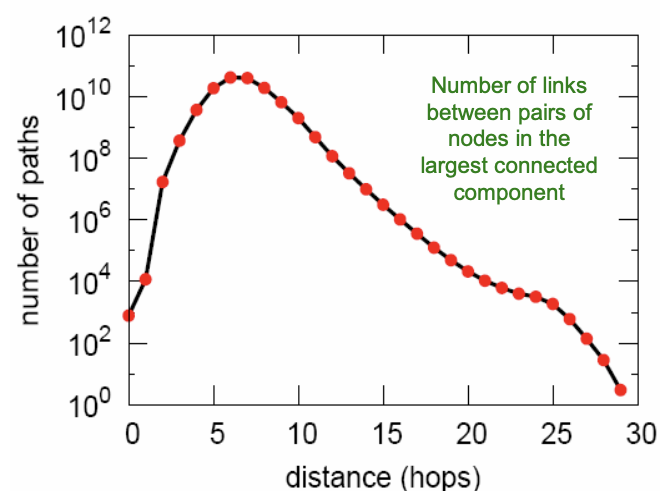
MSN의 Network Properties

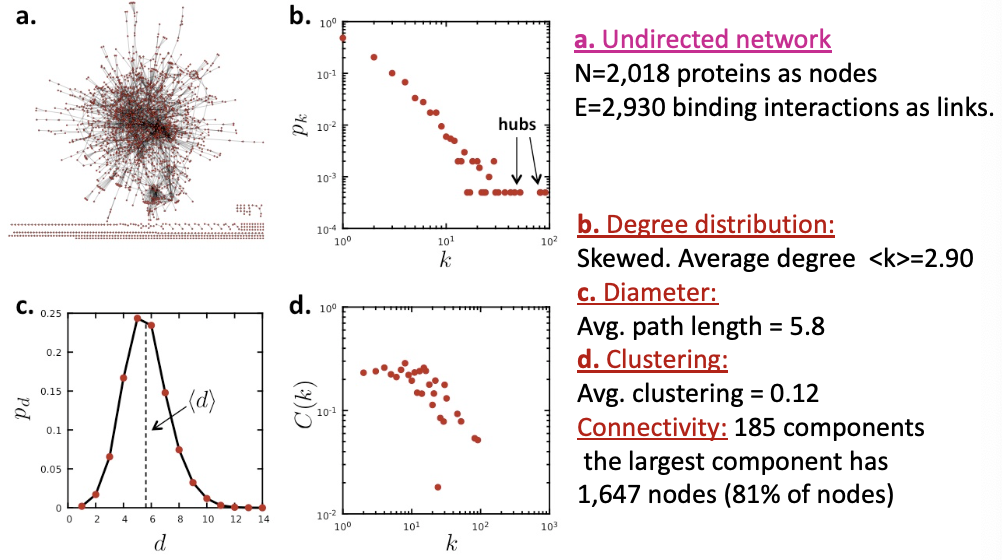
Another example: PPI Network (protein protein international Network)

(다른 도메인인데도 비슷하다!)

3. Erdos-Renyi Random Graph Model

Erdos-Renyi Random Graph Model 을 보겠습니다. 2가지 종류로 나뉩니다.

중점적으로 살펴볼 G_np 는 undirected graph에서 n개의 node들이 있을 때, 각 edge(u,v)의 확률 p가 iid 임을 가정합니다. (independent identically distributed, 상호독립 & 동일한 확률분포 가짐)

이 그래프 모델이 어떤 network를 만드는지 살펴보겠습니다.

Random Graph Model

Random Graph Model은 n개의 노드와 확률 p를 가지지만 그래프를 unique 하게 정의하지는 않습니다. (생성할 때 마다 다른 모양)

그럼 랜덤그래프를 앞에서 배운 4가지 속성으로 평가해보겠습니다.

1. Degree Distribution

random graph model G_np 의 degree distribution은 binomial(이항분포)을 따릅니다.

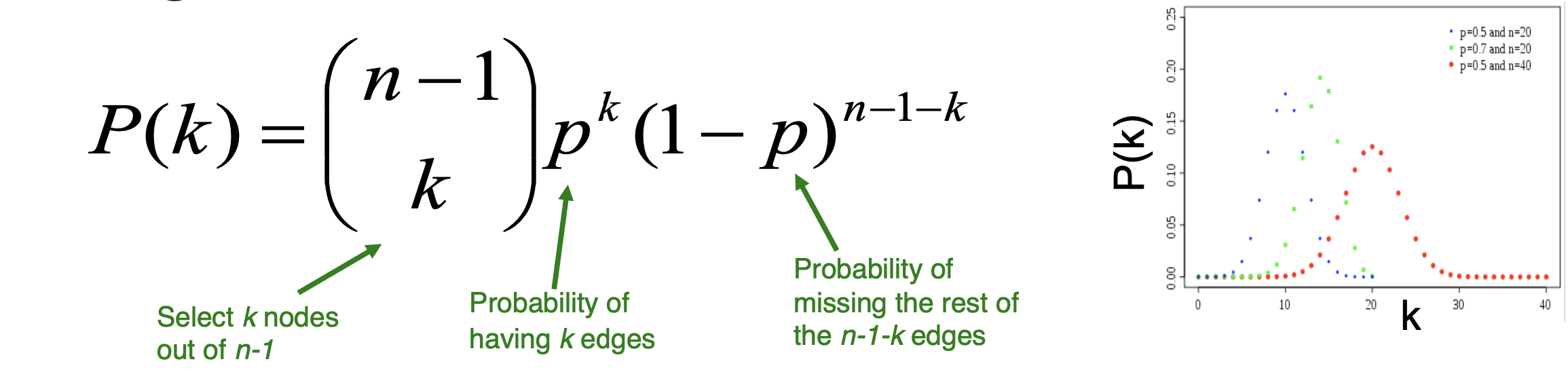
degree k의 평균과 분산도 이항분포의 공식으로 나타낼 수 있습니다.

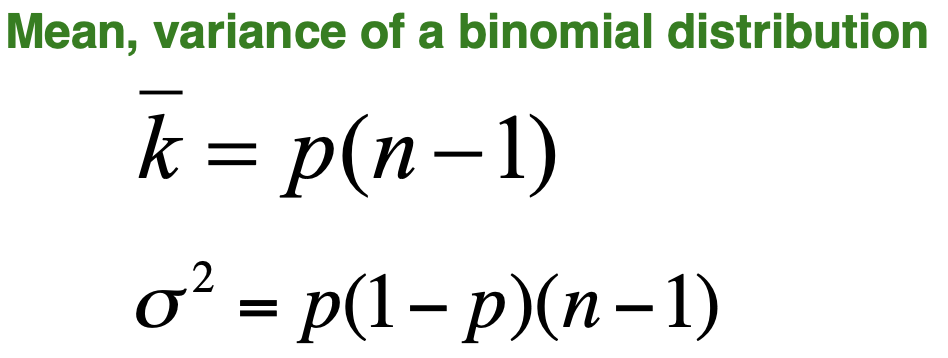
2. Clustering Coefficient

C = 2*e_i / k_i(k_i -1) 임을 기억한다면, e_i의 기댓값과 C_i의 기댓값은 다음과 같습니다.

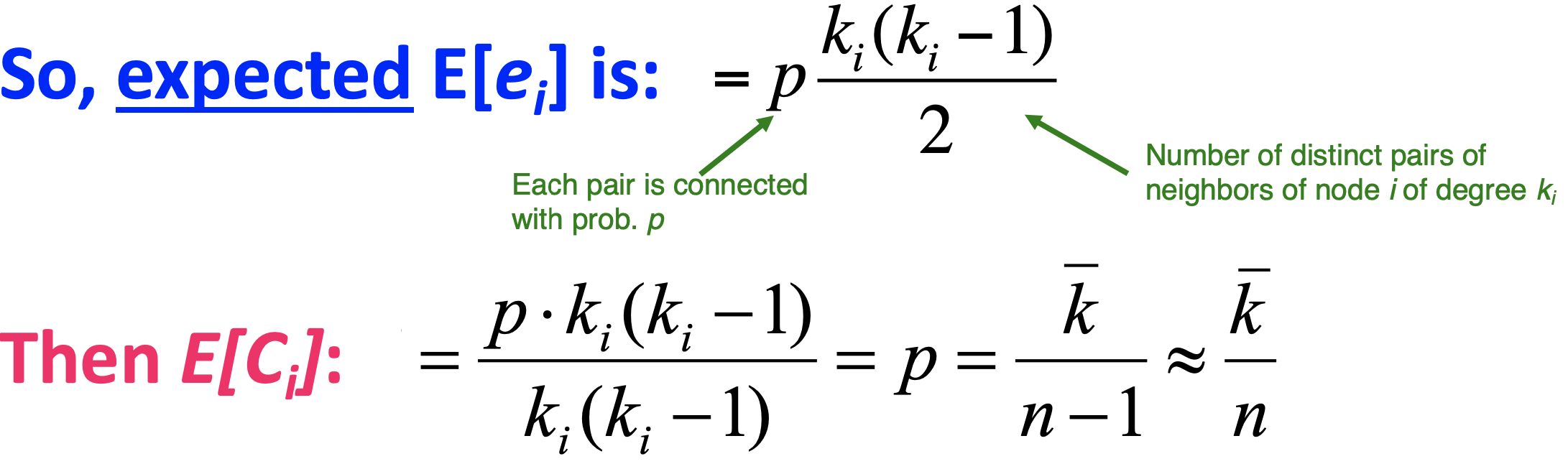
3. Path length

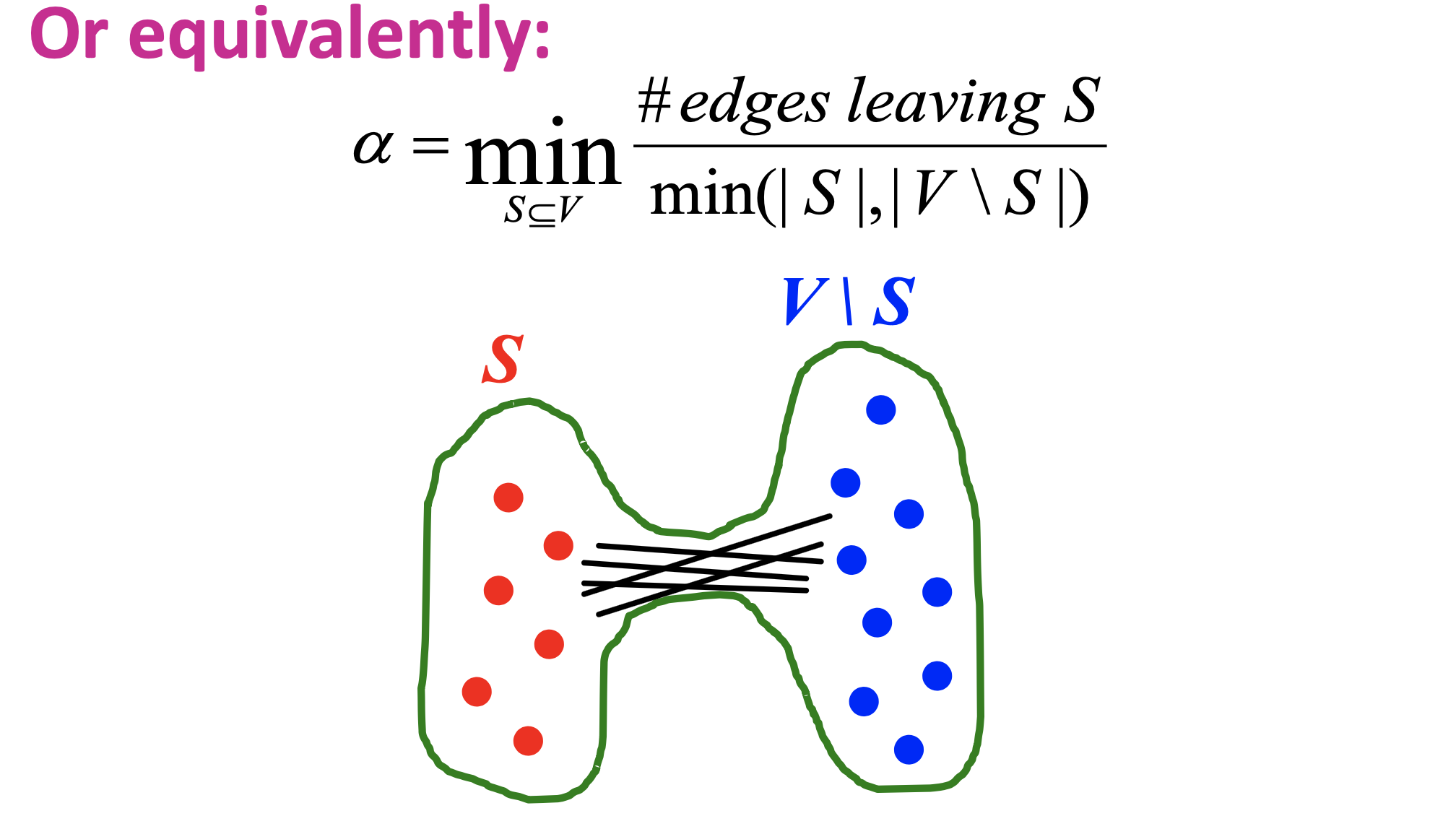
Expansion alpha : Expansion은 subset에서 edge가 퍼져나가는 정도로, 그래프에서 노드 S가 V의 부분일 때, S -> V로가는 edge의 수의 최소값을 Expansion alpha 라고 합니다.

alpha를 다음과 같이 수식화 할 수 있습니다.


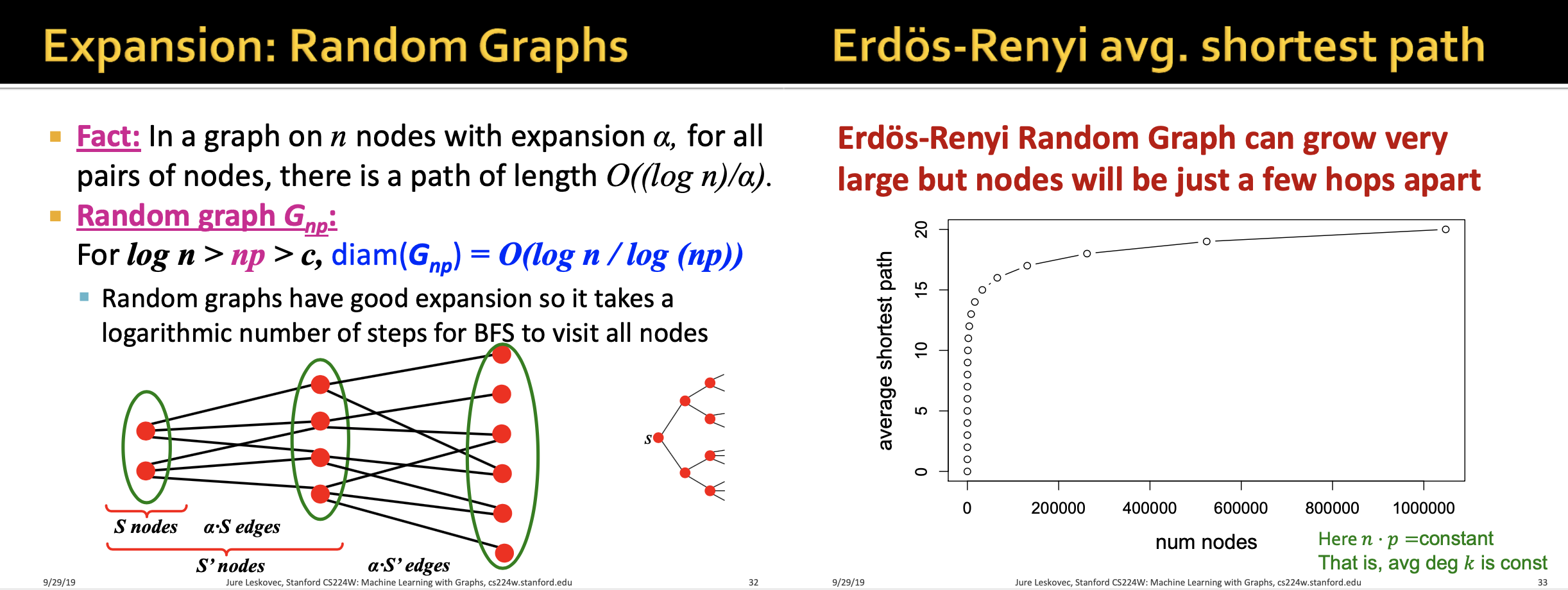
처음 s개의 노드를 정하고 각각의 노드와 (α⋅S) edges로 연결된 노드들을 구한다. 그 다음, 새롭게 연결된 노드들까지 포함하여 S′ 노드들을 다시 하나의 subset으로 보고 (α⋅S') edges로 연결된 노드들을 구한다. 이렇게 모든 노드들을 방문할 때까지 반복하여 path를 구할 수 있다. path length는 O((log n)/α) 다. 우측 그림에서 노드 수가 증가할때 shortest path는 log 함수 형태로 증가함을 볼 수 있다.

즉 그래프 크기에 비해 짧은 경로들을 가지게 된다.

4. Connectivity


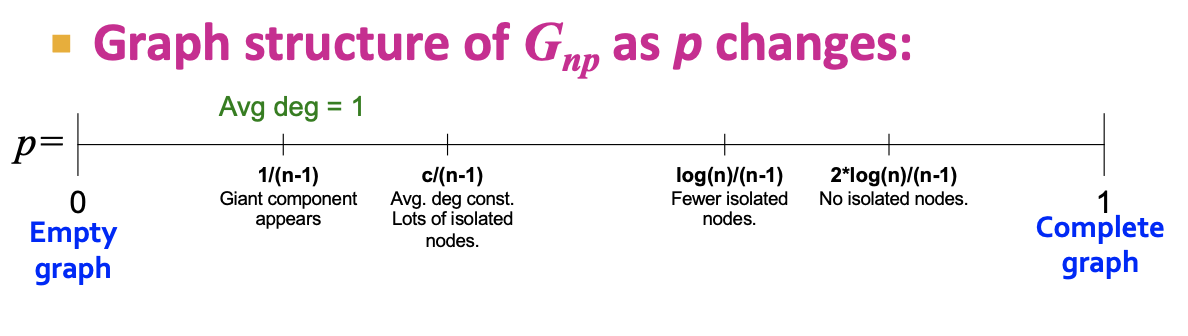
확률 p 에 변화에 따른 랜덤그래프의 구조는 위와 같은데, 확률이 커질 수록 (1에 가까울 수록) 모든 노드가 서로 연결되어 있는 Complete graph가 된다.

5. 비교


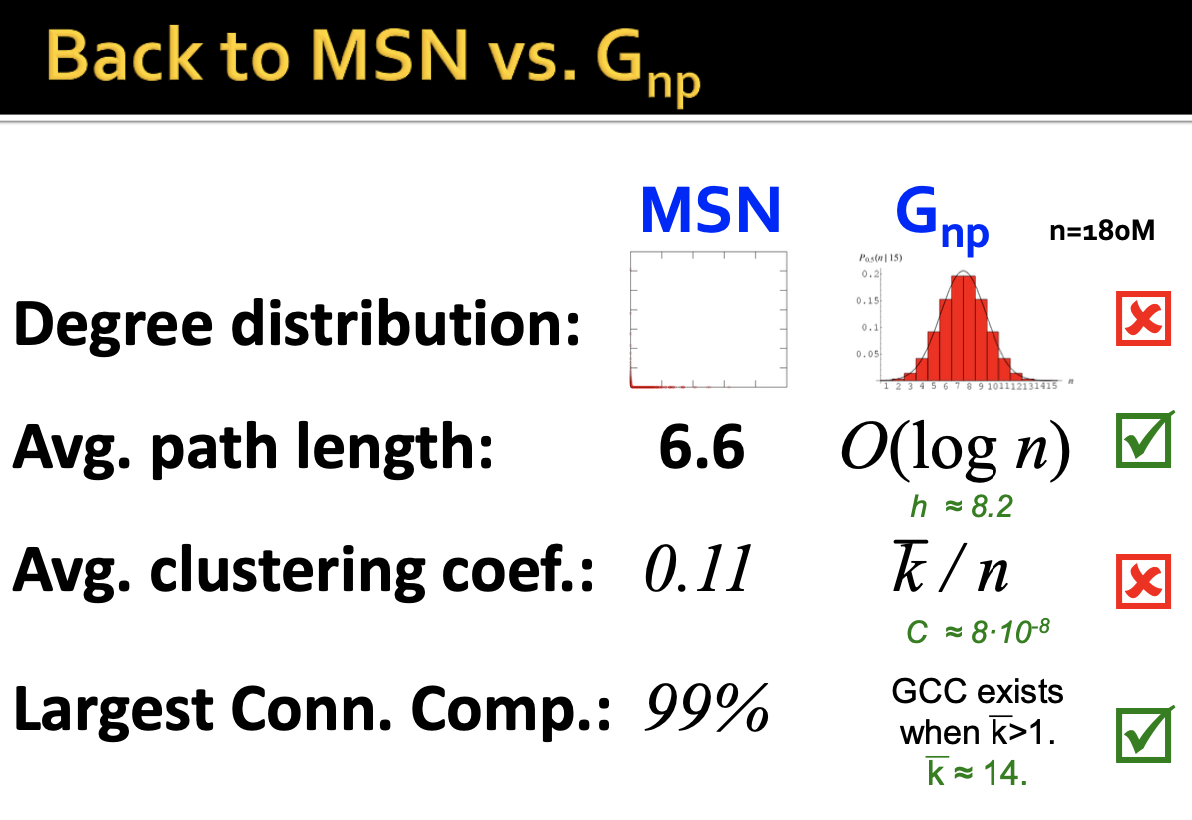
랜덤 그래프 모델과 실제 네트워크 (MSN) 을 비교해보면 Average Path length 와 Largest Connected Component에 대한 속성은 비슷하고 Degree distribution 과 Clustering Coefficient 은 달랐습니다.

Problems with random networks model

  • Degree distribution이 실제 네트워크들과 다름
  • 실제 네트워크의 Giant component는 phase transition을 통해 나타나지 않음
  • local structure 가 없음. (=clustering coefficient가 너무 낮다.)

근본적으로 real world 가 random 이 아니기 때문에 완전히 fit 될리가 없습니다.

4. The Small-World Model


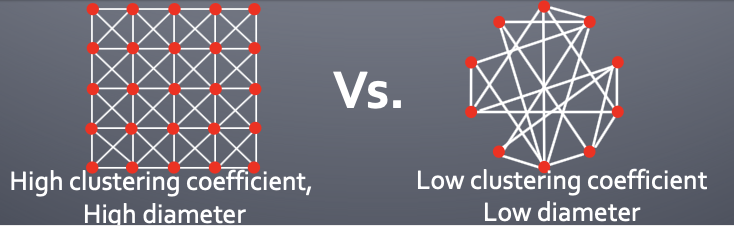
실제 Real world는 random graph model과 다르게 High Clustering을 유지하면서 small diameter를 유지합니다.

이러한 모델을 만들기 위해서 Small-World model 을 설명합니다.

small-world model 중에 Watts-Strogatz 를 살펴봅니다.


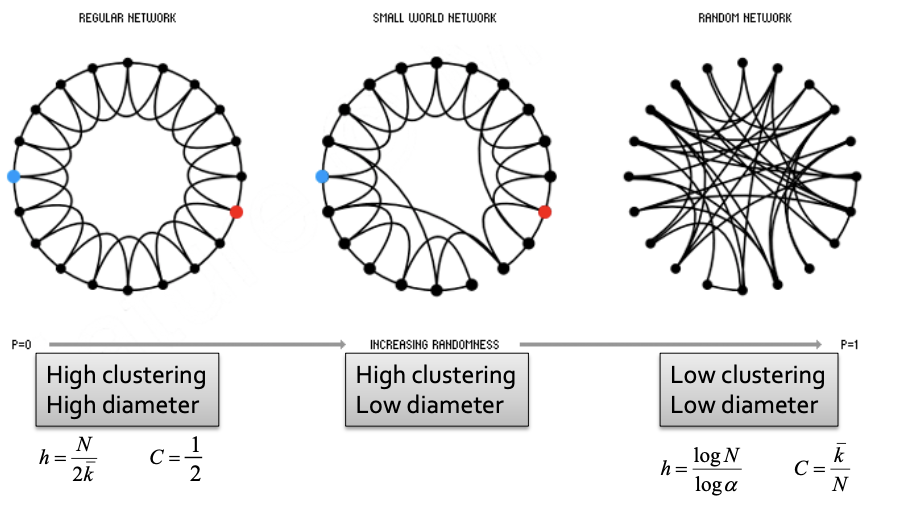
Low-dimensional regular lattice 에서 rewiring을 해준다면 절충되는 그래프를 만들 수 있습니다.

Low-dimensional regular lattice는 주변노드끼리만 이어져있는 네트워크를 의미한다. 즉, High clustering이고 따라서 High diameter입니다.

행운의 편지 전달에서 끼리끼리 그룹의 친구에게만 공유하는 것이 아니라 가끔은 별로 안친한 그룹의 친구에게 전달하는 것과 같습니다.

5. Kronecker Graph Model

오늘 강의의 3번째 모델로는 Kroneckr Graph Model을 살펴보겠습니다.

핵심 아이디어는 Self-similarity (자기 복제)를 통한 재귀적 그래프 생성입니다.

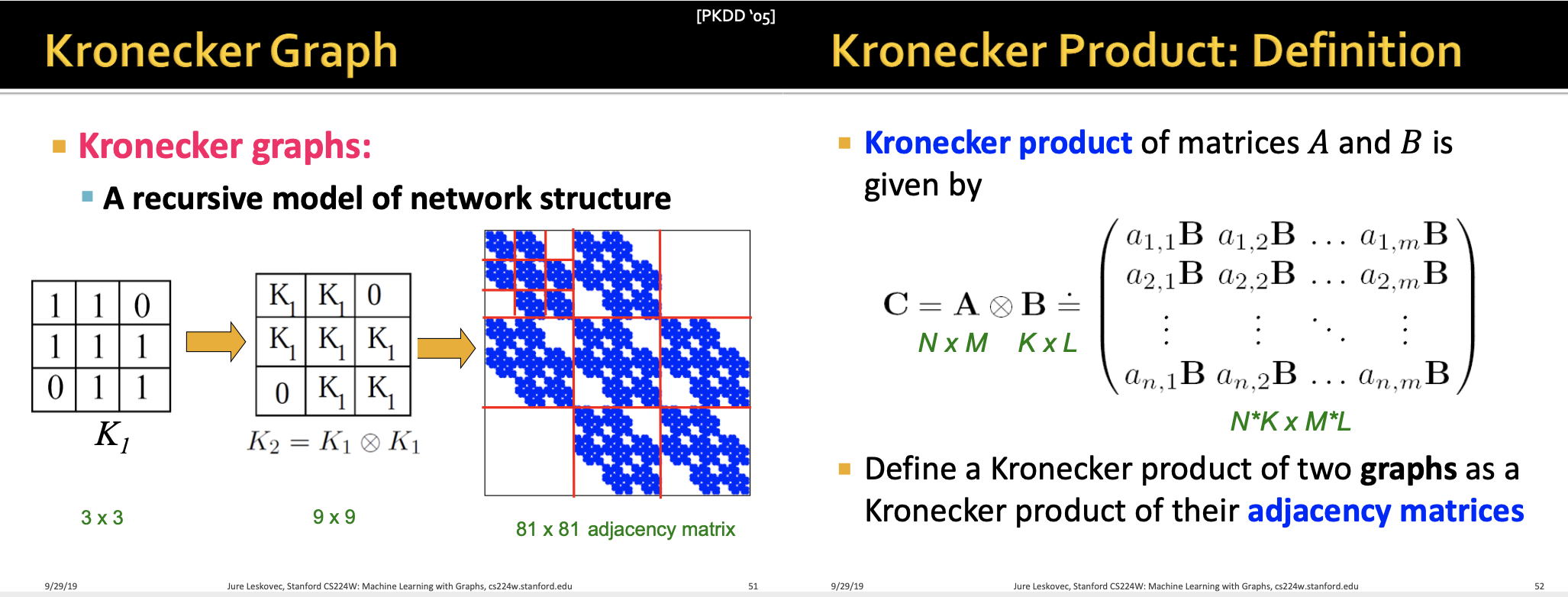
Kronecker Graph의 구조는 위와 같이 recursive model 입니다.

Kronecker Product : 인접행렬간의 행렬곱을 위와 같이 정의합니다.

Stochastic Kronecker Graphs

0,1 이 아니라 확률적으로 이루어진 Stochastic Kronecker Graphs는 아래와 같이 생겼는데, 하나의 graph를 생성하기 위해서 사건을 너무 많이 시행해봐야하는 문제점이 있습니다. (동전 던지기를 너무 많이 해봐야함)

-> 이는 노드 수가 증가하면서 run time 에 많은 영향을 주기 때문에 빠르게 생성하는 방법을 고안했습니다.

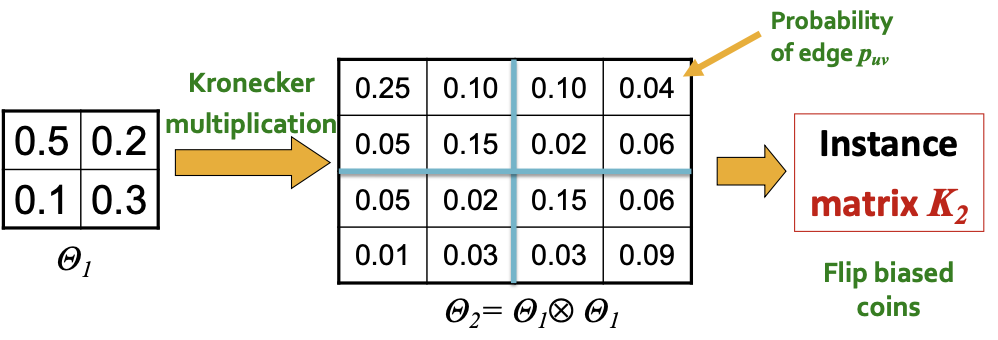
Stochastic Kronecker Graphs

Drop Edge : 빠르게 Kronecker graphs를 만드는 방법은 그래프에 edge 를 하나씩 'drop'하는 것입니다. (재귀적인 특성 이용)


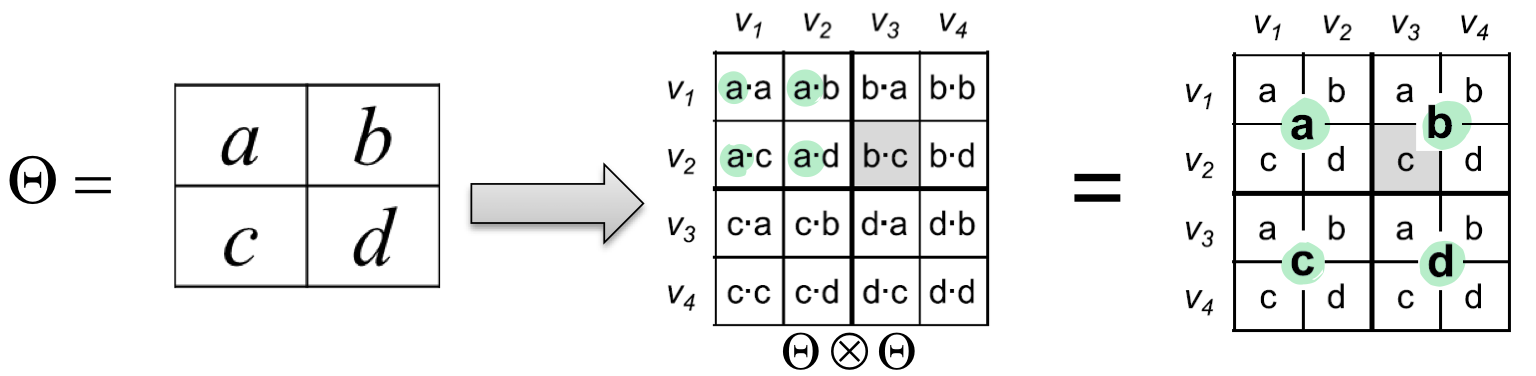
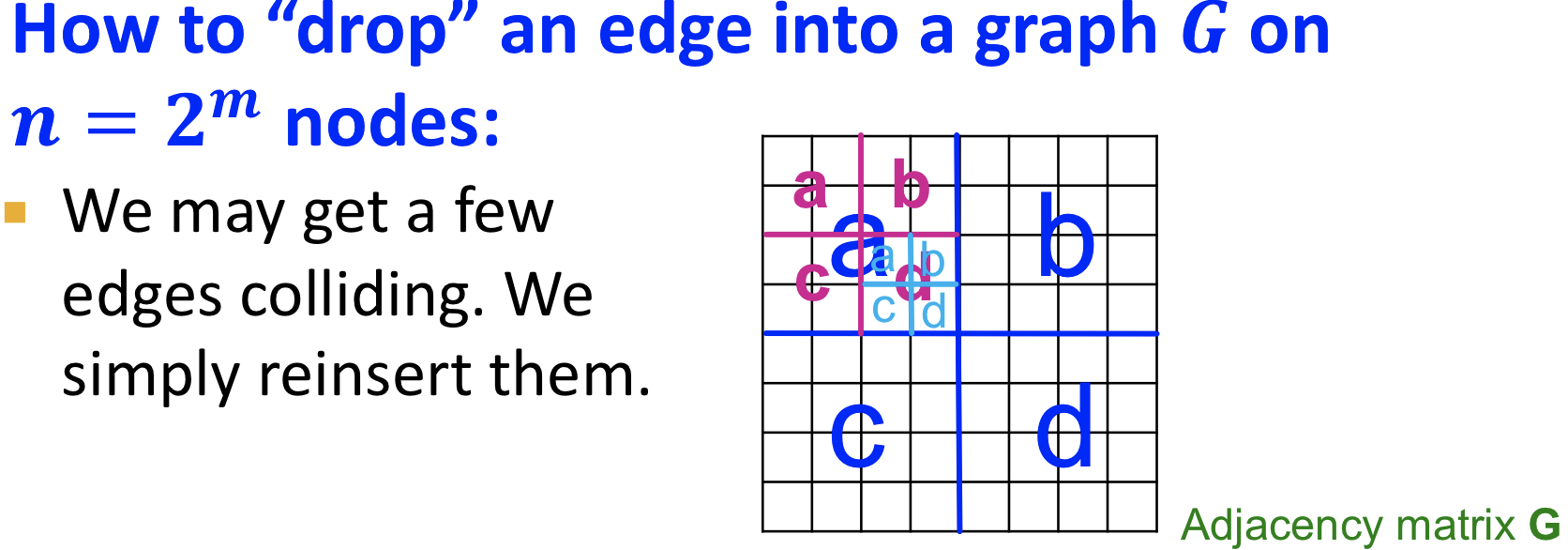
재귀적으로 drop을 반복합니다.

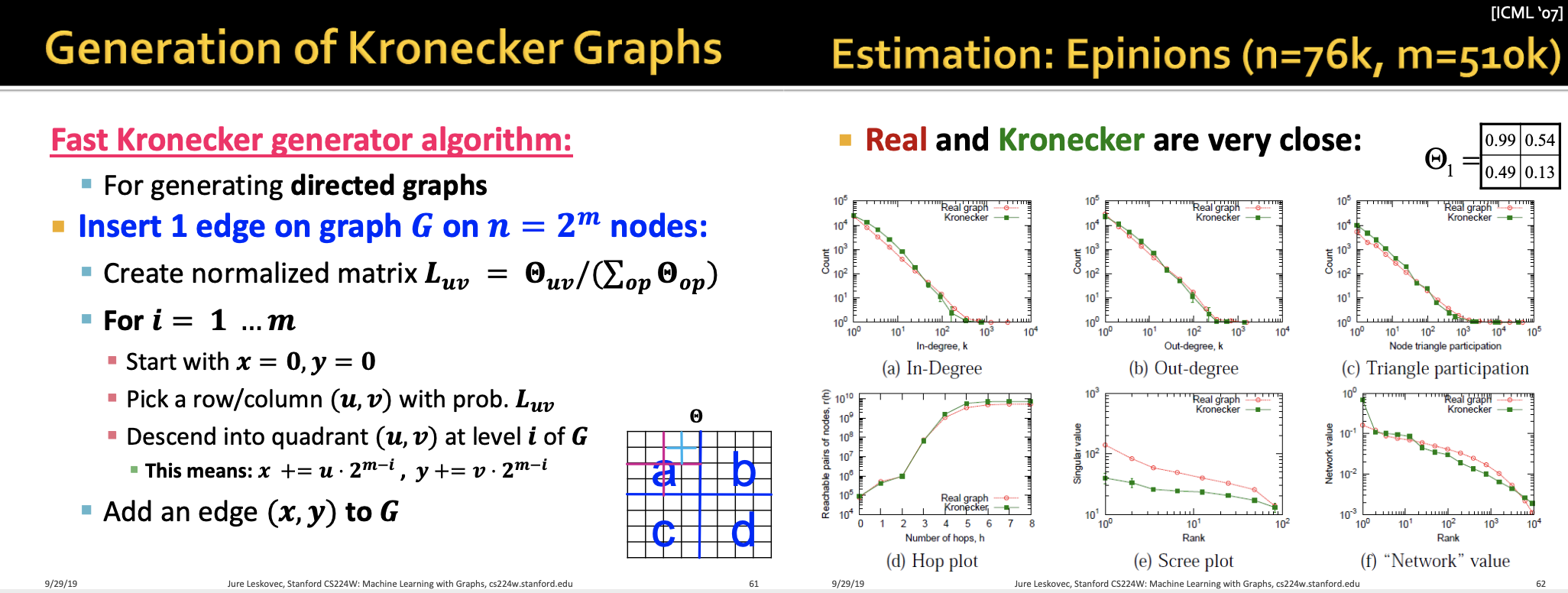
Fast Kronecker generator algorithm을 정리하면 위와 같습니다.
신기하게도 Kronecker 는 real-world 와 아주 닮아있습니다.


결론적으로 Kronecker Graph Model 은 확률적인 속성을 가지고, 적은 파라미터를 사용해서 real world에 잘 fitting 시킬 수 있다는 장점이 있습니다.

(Kronecker의 MLE와 자세한 유도는 http://www.cs.cmu.edu/~jure/pub/kronecker-cornell-Sept08.pdf
여기에 나와있습니다.)

6. Summary

Graph Model의 4가지 속성에 대해서 배우고, 실제 예시에 대입해봤습니다.
실제 real-world를 설명할 수 있는 graph model 만들기 위해서 random graph model, small-world model, kronecker graph model에 대해서 배웠습니다.

Reference

https://tobigs.gitbook.io/tobigs-graph-study/chapter2.
https://leejunhyun.github.io/deep%20learning/graph/2019/03/05/CS224W-02/

profile
tobigsGNN
2021 투빅스 GNN 스터디
이전 포스트

1. Introduction; Structure of graph

다음 포스트

3. Motifs and Structural Roles in Networks

5개의 댓글

comment-user-thumbnail
.
2021년 2월 19일

Network Properties

  1. Degree distribution (p(k)) : node에 연결 된 엣지의 갯수가 degree k 라고 할 때, 무작위로 선택한 node 가 k개의 차수를 가지고 있는 확률
  2. Path (경로) : 각 노드가 다른 노드와 연결된 연속성
  3. Clustering Coefficient (결집계수) : 해당 노드와 다른 노드들이 얼마나 잘 연결되어 있는지를 나타내 주는 값
  4. Connectivity (연결성) : 연결된 구성요소 중에 가장 큰 크기

Random Graph Model

가장 easiest 하고 simple 한 graph model, 심플하고 랜덤하게 (unique하지 않게 그때그때마다) 그래프를 생성
GnpG_{np} : undirected graph에서 n개의 node들이 있을 때, 각 edge(u,v)의 확률 p가 iid 임을 가정

  1. Degree distribution : binomial
  2. Clustering Coefficient : mean(k) / n
  3. Path length
    • Expansion alpha : 그래프에서 S가 V의 부분일 때, S->V로 가는 edge 수의 최솟값
    • S’ = α⋅S, 모든 노드들을 방문할 때까지 반복 = 그래프 크기에 비해 짧은 경로들을 가지게 됨
  4. Connectivity : p값에 따라 랜덤그래프 구조가 달라지고, 1에 가까워 질수록 complete graph 됨

The Small World Model

  • real world = high clustering & small diameter (!= random graph)
  • Rewire : 낮은 dimension의 lattice(격자)에서 시작해서 high clustering coef 만들고, 랜덤으로 서로 연결된 것을 끊어서 다른 점에 연결

Kronecker Graph Model

  • 네트워크가 Self-similarity의 특성을 갖고 있음에 착안하여, Recursive하게 네트워크 구조를 형성
  • 재귀적으로 Drop-edge 반복

리뷰 썼어욤 일타강사님 좋은 강의와 댓글 감사함니당 ^_^ ~

답글 달기
comment-user-thumbnail
청강생
2021년 2월 19일


이번 강의는 일반적인 네트워크의 성질과 이를 활용한 random graph model에 대해 배울 수 있었습니다.

    네크워크를 평가하는 지표에는 (1) Degree Distribution (2) Path length (3) Cluster Coefficient (4) Connected components 의 4가지가 있습니다. MSN Messenger의 예시에서는 네트워크의 평균 차수 분포가 네트워크가 커짐에 따라 로그 스케일로 줄어듦을 알 수 있습니다. Path는 숫자가 커지더라도 distance는 30을 넘지 못하고 있었습니다. SNS에서 30명만 거치더라도 모든 사람과 연락을 할 수 있다는 뜻이겠죠? 이렇게 현실세계에서의 네트워크는 굉장히 특이합니다.
   많은 연구자가 실제 네트워크와 비슷한 것을 생성해보고 싶은 욕구가 생겼나봅니다. (1) edge 연결확률이 p로 iid인것과 uniform한 확률분포 2가지를 활용한 Random world (2) 차수분포와 clustering coefficient가 실제 네트워크와 비슷하지 않는 random world를 보완하기위해 edge를 rewiring하는 Small world (3) 재귀적으로 그래프를 생성하는 Kronecker Graph 등의 생성모델이 나타납니다. 네트워크 이론과 다양한 네트워크 생성 모델을 소개해주시고 좋은 발표 진행해주셔서 감사합니다.

답글 달기
comment-user-thumbnail
김태욱
2021년 2월 19일

Network의 속성과 다양한 그래프 모델에 대해 배웠습니다.

Network Properties

  • Degree distribution, P(k): node에 연결 된 엣지의 갯수가 degree k 라고 할 때, 무작위로 선택한 node 가 k개의 차수를 가지고 있는 확률
  • Paths in a Graph(경로): 각 노드가 다른 노드와 연결된 연속성
  • Clustering Coefficient(결집계수): 노드 간 서로 연결되어 있는 정도
  • Connectivity(연결성): 연결된 구성요소 중에 가장 큰 크기이며 BFS(너비우선탐색) 알고리즘으로 찾음.

Random Graph Model
Random Graph Model은 n개의 노드와 확률 p를 가지지만 그래프를 unique 하게 정의하지는 않음

  • Degree Distribution: binomial(이항분포)을 따름

  • Clustering Coefficient:

    • E[ei]=p⋅ki(ki−1)/2E[e_i] = p·k_i(k_i-1)/2
    • E[Ci]=mean(k)/nE[C_i] = mean(k)/n

  • Path length

    • Expansion alpha : Expansion은 subset에서 edge가 퍼져나가는 정도로, S -> V로가는 edge의 수의 최소값
    • 처음 s개의 노드를 정하고 각각의 노드와 (α⋅S) edges로 연결된 노드들을 구하고 이 과정을 반복하여 path를 구한다. 그래프 크기에 비해 짧은 경로를 가진다.

  • Connectivity: 확률이 커질 수록 (1에 가까울 수록) 모든 노드가 서로 연결되어 있는 Complete graph가 됨

  • Problems with random networks model

    • Degree distribution이 실제 네트워크들과 다름
    • 실제 네트워크의 Giant component는 phase transition을 통해 나타나지 않음
    • local structure 가 없음. (=clustering coefficient가 너무 낮다.)

Small-World Model
실제 Real world는 random graph model과 다르게 High Clustering을 유지하면서 small diameter를 유지

Kronecker Graph Model

  • 핵심 아이디어: Self-similarity (자기 복제)를 통한 재귀적 그래프 생성

제가 아직 많이 부족해 이런 기초를 알려주는 강의가 많이 도움이 됐습니다 :)

1개의 답글
comment-user-thumbnail
신민정
2021년 2월 20일

이번 강의는 graph의 속성과 정량적 측정법에 관한 내용이었습니다.

How to measure a network

  • Degree distribution P(k)=Nk/NP(k) = N_k/N : edge의 차수 분포.
  • 경로 Path : 각 노드가 다른 노드와 연결된 연속성, path로 distance, network diameter, average path length를 구할 수 있다.
  • Clustering Coefficient Ci=(2e)/ki(ki−1)C_i=(2e)/{k_i(k_i-1)}
  • Connectivity : Largest compenent

Erdos-Renyi Random Graph Model GnpG_np

undirected graph에서 n개의 node들이 있을 때, 각 edge(u,v)의 확률 p가 iid임을 가정합니다.
degree distribution은 binomial을 따르고, clusterng coefficient의 기댓값은 E[Ci]≈kˉ/nE[C_i] \approx \bar{k}/n입니다. network가 얼마나 하나로 잘 뭉쳐있는지는 expansion으로 나타낼 수 있습니다.
Real world와 비교하였을 때 clustering coefficient가 낮고, degree distribution의 차이가 있습니다.

Small-World Model - Watts-Strogatz

random graph model과 다르게 High clustering&small diameter을 유지합니다.
regular network와 random network의 절충안으로 볼 수 있습니다.

Kronecker Graph Model

self-simiarity를 통한 recursive model입니다. -> Kronecker product로 network 확장/생성
computation을 고려한 optimazation방법 중 하나로 Kronecker product시에 Drop을 사용할 수 있습니다.

답글 달기