
Intro
Epidemics vs Cascade Spreading
epidemic spreading
- 의사결정이 결핍되어있음
- 감염의 과정이 매우 복잡하고 눈에 보이지 않습니다.
당연하게도 높은 감염률이면 질병이 퍼져나가게 되며, 낮은 감염률이면 질병이 소멸하게 됩니다.
Probabilistic Spreading Models
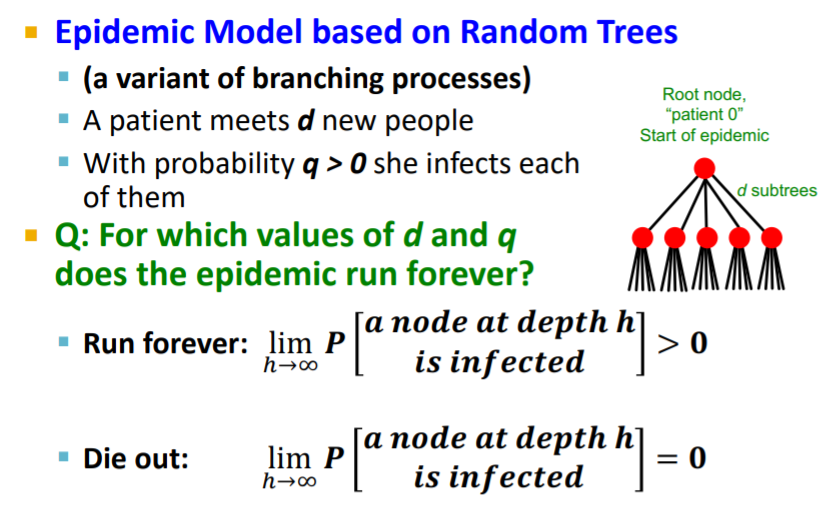
'd'를 자식노드의 수 'q'를 감영확률이라고 가정한다면, 전염벙이 지속되는 d와 q값은 무엇일까요?
임의의 노드 h에서 한 노드가 감염될 확률이 0보다 크다면 우리는 전염병이 확산된다고 말할 수 있습니다. 임의의 노드 h가 무한대로 갈 때 (시기가 계속된다면), 전염병은 지속되고 있다고 말할 수 있을 겁니다.

그렇다면, 우리는 임의의 노드 h에서 한 노드가 감염될 확률을 구한다면, 전염병의 지속여부에 대해서 파악할 수 있습니다.
임의의 노드 h에서의 확률은 다음과 같이 구할 수 있습니다. 이전 노드에서 나온 자식노드들이 모두 감염되지 않을 확률을 1에서 빼면 됩니다.
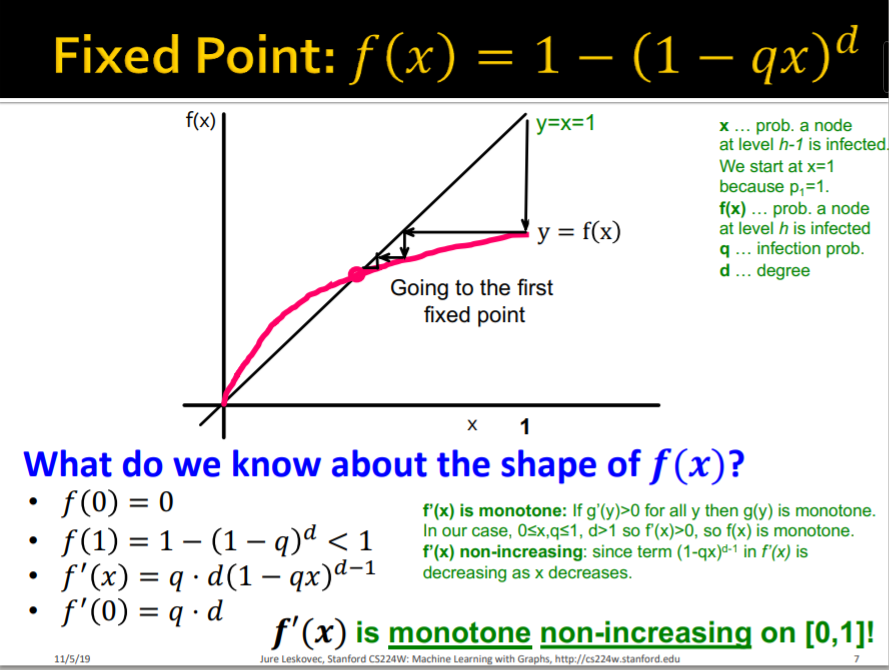
결국 root 노드 (초기감염자)의 확률 1에서 시작하여, 확률이 점차 낮아지는 형태의 함수가 만들어집니다.
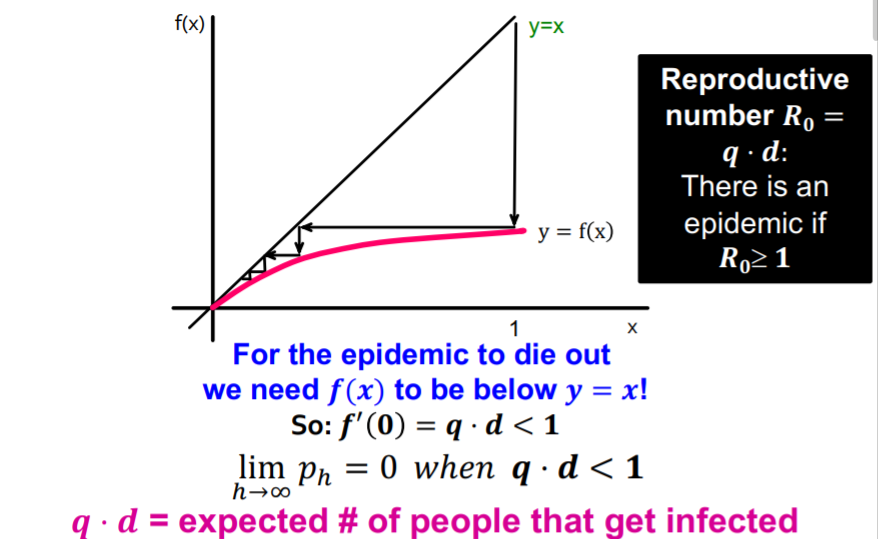
여기서 중요한 것은 변화율 qd에 따라 전염병이 확신이 될지 안될지 결정할 수 있다는 점입니다. qd는 감염된 사람들의 기대평균 수를 나타내는 값으로, qd가 1보다 작다면 x=p가 0으로 수렴하게 되므로 0으로 수렴하게 됩니다.

Applicaition: Social cascades on Flickr and estimating R0 from real data
Dataset
- Users can be exposed to a photo via social influence (cascade) or -external links
- Did a particular like spread through social links
No, if a user likes a photo and if none of his friends have previously liked the photo
Yes, if a users likes a photo after at least one of her friends liked the photo-> Social cascade - Example social cascade: A->B and A->C->E
- Flickr social network
Users and connected to other users via friend links
A user can like/favorite a photo - Data:
100 days of photo likes
Number of users : 2 million
** 34,734,221 likes on 11, 267, 320 photos

R0를 추정하는 방법에는 두가지 방법이 있습니다. Estimate of R0 방법과 Empirical R0를 획득하는 방법입니다. Estimate of R0의 경우, 실제와 유사한 값을 가지기 위해서 보정상수(Correction factor)을 곱해주어 다음 값을 구해줍니다. Empirical R0의 경우, start node를 기반으로 cascade 과정을 통해 직접 감염된 노드를 세주는 것입니다.
확실하진 않지만, Estimate of R0는 전체적인 연산과정을 통해 R0를을 추정하는 것이며, Empirical R0는 단편적인 부분만 보고 R0를 유추한다는 것으로 이해됩니다.
여기서는 Empirical R0가 Estimate of R0를 얼마나 따라갈 수 있을지 확인해보는 것이 포인트 입니다. 만약 잘 따라간다면, 단편적인 부분 (부모노드)만 보고서 해당값을 유추할 수 있을 것입니다.
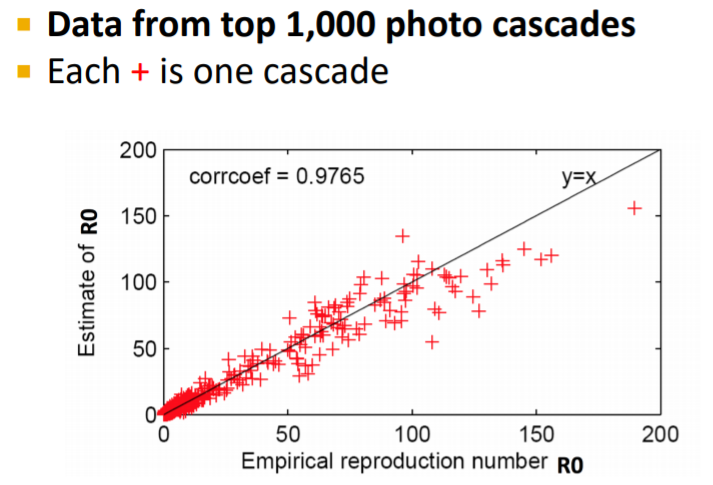
결과적으로 높은 상관관계가 나타나고 있습니다.
Epidemic models
Virus Propagtion에는 두 개의 파라미터가 있으며,
Birth rate: probability that an infected nieghbor attacks
Death rate: Probability that an infected node heals
Epidemic models에는 SEIR, SIR, SIS Model 등이 있습니다.
More Generally: S+E+I+R Models
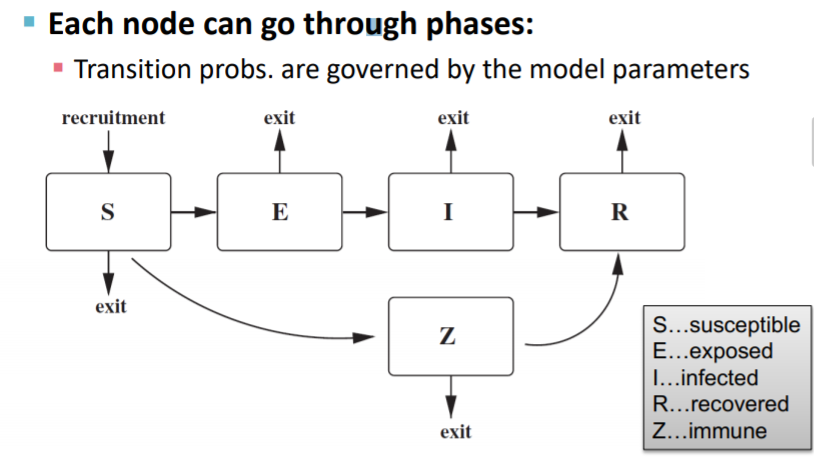
각각 노드가 갈 수 있는 상태를 나타낸 것입니다.
SIR Model
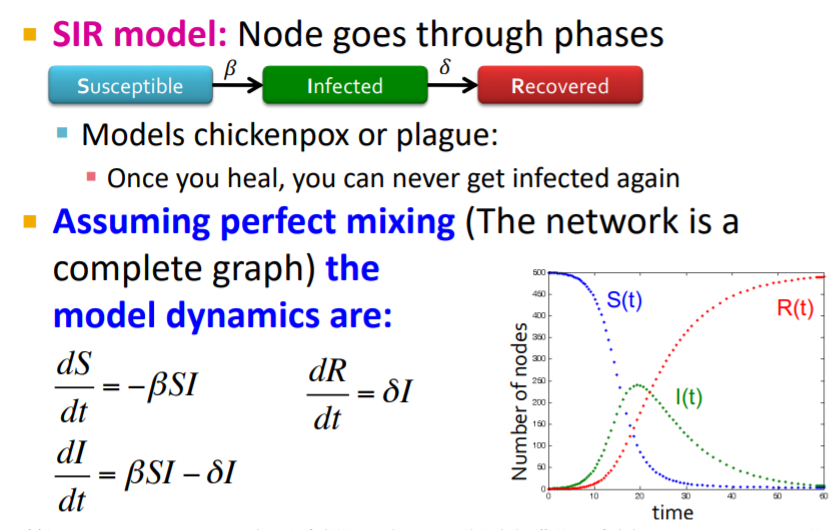
Susceptible people changing (-BSI): 취약층에서 감염된 사람들만큼 줄기 때문에 -의 부호가 붙습니다.
SIS Model
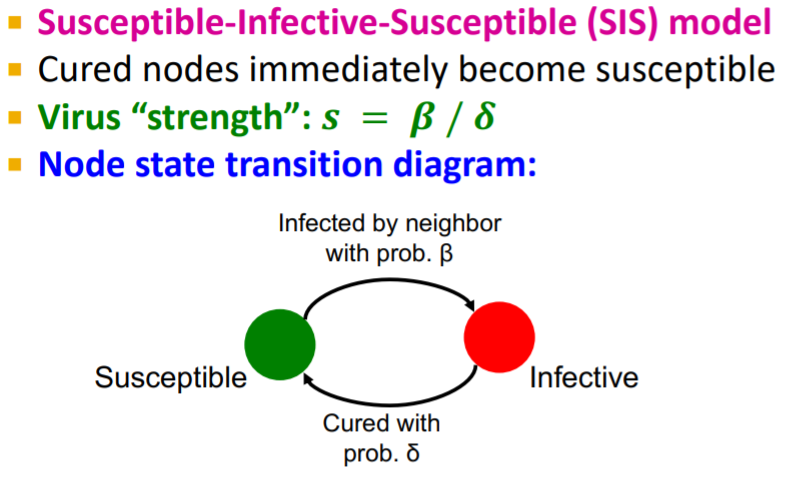
virus "strength"을 측정은 다음과 같이 측정할 수 있습니다.
SIR모형과의 차이점은 unsusceptible people changing의 값이 다르다는 점입니다. 이는 노드가 다시 susceptible 상태로 이동할 수 있음을 나타내고 있습니다.

당연하게도, 치료확률 (cured value)이 훨씬 더 커지게 되면, 전염병은 더이상 확산되지 않을 것입니다. 위의 그림은 다음과 같은 논리를 수식으로 표현하고 있습니다.
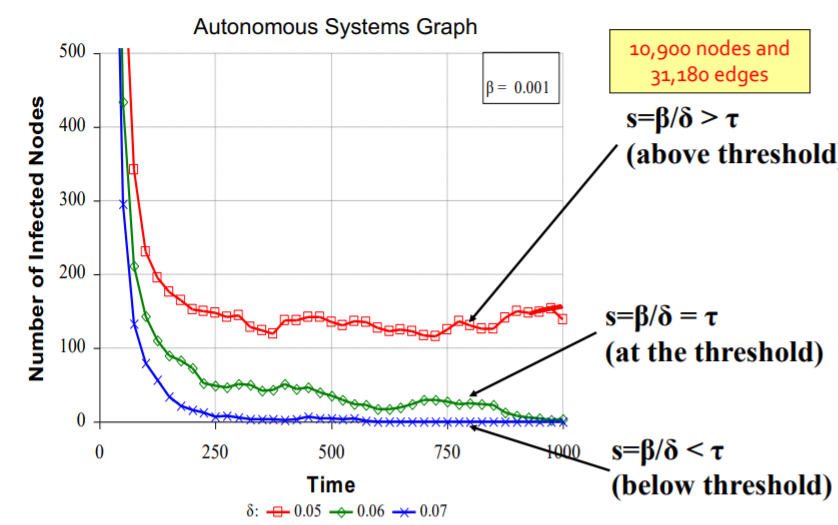
threshold 값을 넘는다면 바이러스는 지속되게 됩니다. 그렇다면 주어진 그래프에서 Epidemic threshold (tau)를 어떻게 구할 수 있을까요? (증명과정은 여기서 생략합니다.) 결론적으로, 가장 큰 고유값의 역수의 값으로 Epidemic threshold를 규정할 수 있습니다.
Application: Rumor spread modeling using SEIZ model
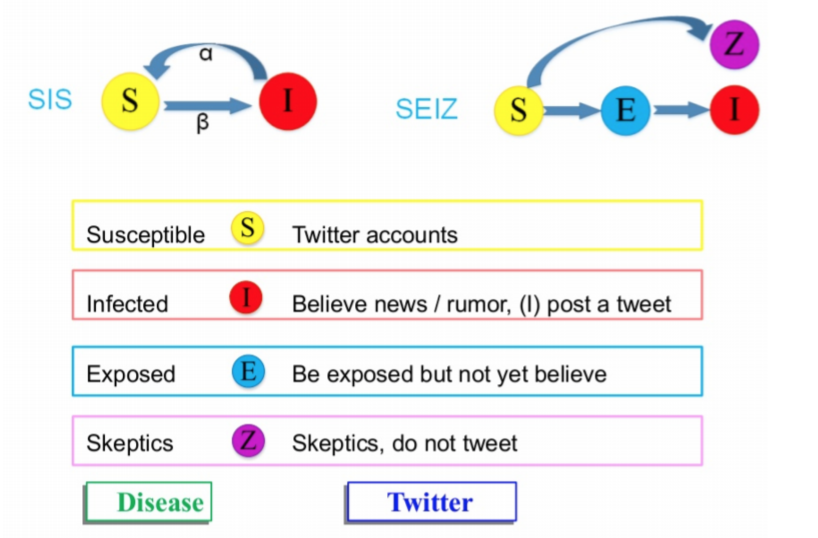
루머의 확산 == 질병의 확산
S: 트위터 계정
I: 루머/뉴스를 믿거나 리트윗한 경우
E: 루머/뉴스를 마주하였으나, 그것을 아직 믿지 않은 상태
S: 루머/뉴스를 믿지 아니하는 것
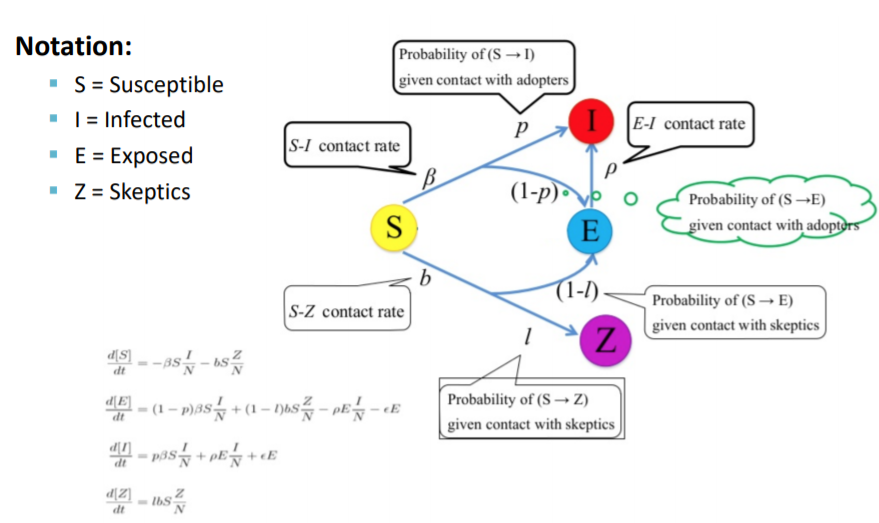
Susceptible의 변화율만 본다면,
SI: S에서 I로의 이동과 파라미터(contact rate) B
SZ: S에서 Z로의 이동과 파라미터(contact rate) b
Susceptible에서는 유입되는 것은 없고, 유출되는 것만 있으므로, 둘다 -의 부호를 가지게 됩니다.
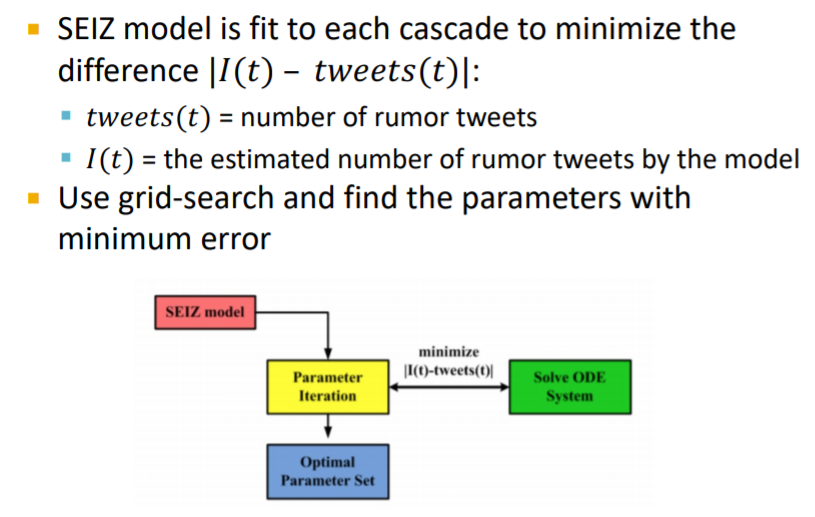
그리드 서치를 통해 실제 rumor의 tweets 수와 모델이 예측한 rumor tweets 수의 차이를 줄이면서 파라미터들을 추정하게 됩니다.
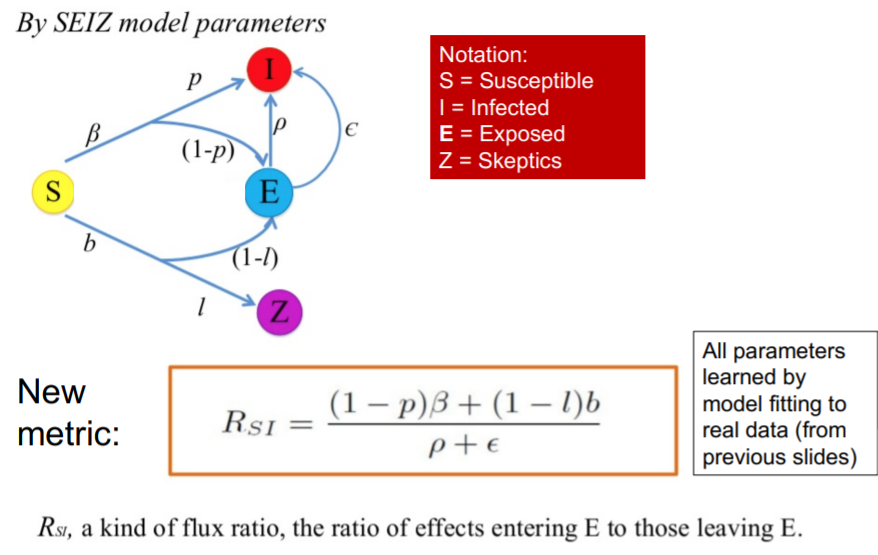
연구자들은 다음과 같은 metric에 대해서 흥미를 가지고 있다고 말합니다. 해당 RSI는 S에서 E로 이동하는 사람의 수와 E에서 I로 이동하는 사람 수의 비율입니다.
비유하자면, 환자가 일상생활에서 병에 노출(Exposed)되는 속도와 노출된 환자가 실제 감염(Infected)되는 속도에 대해서 파악하고자 한 것으로 보입니다.
한 실험에서의 결과를 바탕으로 봤을 때, Rumor의 경우 Real news보다 해당 값의 비율이 높았다고 말하고 있습니다. 그 만큼 Rumor의 경우, 빠르게 사실로 받아지는 것을 알 수 파악해볼 수 있었습니다.
Independent Cascade Model
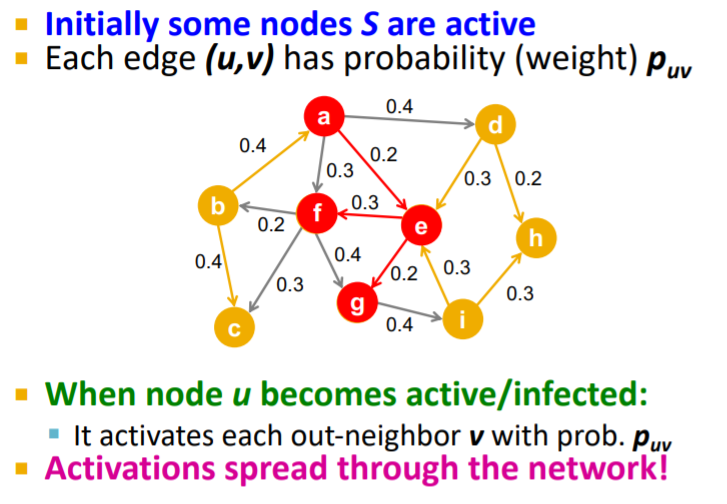
edge (u,v) 는 확률값을 가지고 있으며, 다른 edge들과 독립적입니다.
즉, 한번의 edge마다 동전던지기를 1회 수행하는 것처럼 독립사건이라는 뜻입니다.
하지만, 실제 데이터로부터 이 weight들을 모두 추정하는 것은 굉장히 어렵습니다. 또한, 이 weight들을 모두 동일하게 취급하는 것 역시 너무 simple한 모델이 되어버립니다. 그렇다면 어떻게 이 문제를 해결할 수 있을까요?
Exposures and Adoptions
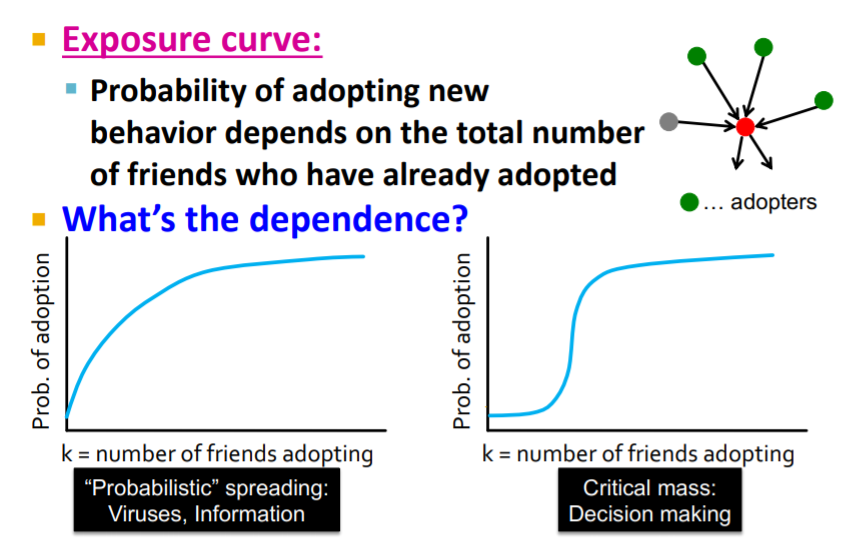
결국, 새로운 행동(전염)의 전파 여부는 이미 행동(전염)이 전파된 주변 노드의 수에 의존하는 것을 파악해볼 수 있습니다.
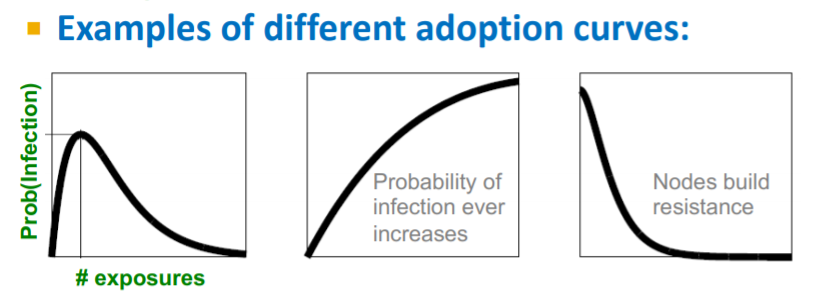
이외의 다양한 형태의 curves들이 존재할 수도 있습니다.
첫번째 그림같은 경우, 광고를 예시로 들을 수 있습니다. 광고의 한두번 노출됐을 때, 구매량이 높게 나타나나, 이후 지속적인 노출은 더이상의 구매량을 증가시키지 못하는 경우를 흔히 찾아볼 수 있습니다.
Twitter Example
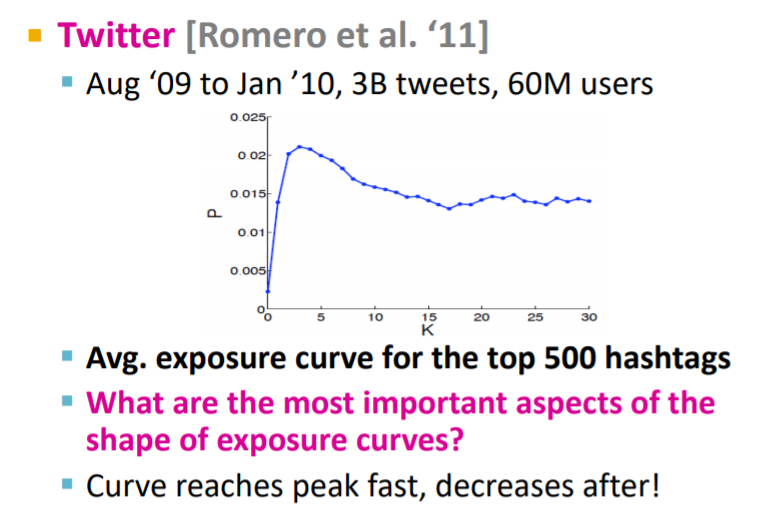
해당 실험은 500개의 hastags에 대해 얼마나 노출되었으며, hashtags에 노출된 뒤, 해당 hastags를 얼마나 사용했느냐 측정한 것입니다. 결과적으로 그래프는 다음과 같이 나타나고 있습니다. 일정시점에서 증가하다가 peak를 찍고, 감소하는 추세를 보이고 있습니다.
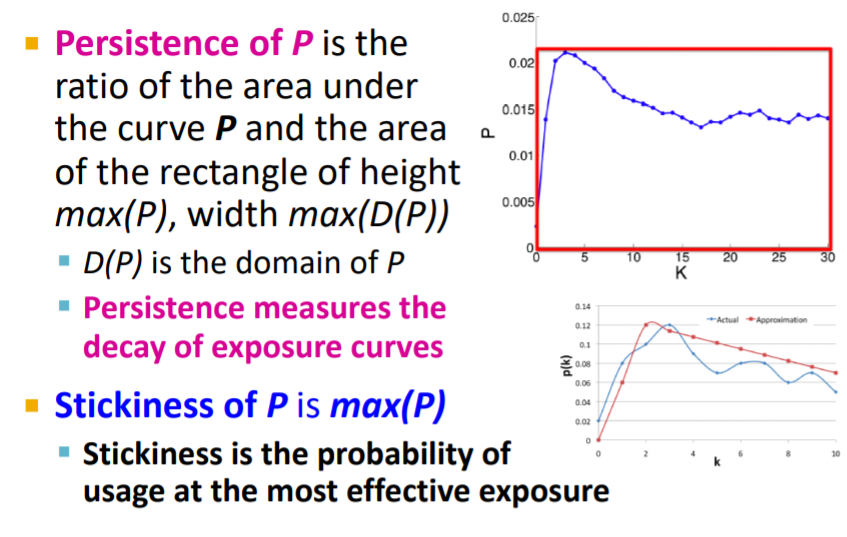
우리는 여기서 persistence의 개념을 파악할 수 있습니다. 만약 가장 높은 peak 점을 찍고 난 후에도 그래프의 곡선이 낮아지지 않는다면 해당 그래프는 지속성이 크다고 말할 수 있을 것입니다. 즉, persistence가 높다고 말할 수 있습니다. 우리는 이를 그래프의 아래의 면적을 통해서 파악할 수 있습니다.
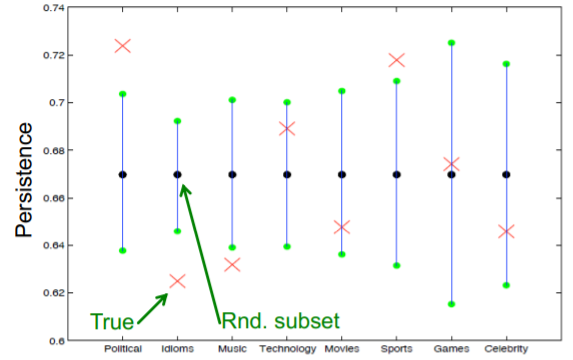
8개의 카테고리에 대해 persistence를 측정한 결과를 보면, Politics와 Sports가 높은 persistence를 가지고 있는 것으로 확인할 수 있었습니다.
8개의 카테고리에 대해 stickiness를 측정한 결과를 보면, Music의 경우, stickiness가 높게 나타나는 것으로 파악해볼 수 있습니다.
3개의 댓글
13강. Probabilitic Contagion and Models of Influence
오늘은 포기를 모르는 홍정님께서 13강. Probabilitic Contagion and Models of Influence 에 대해서 강의해주셨습니다. 저번 12강에서 Cascade 가 의사결정이 되지 않는 경우는 probabilitic 한 모델을 사용한다고 했는데, 역시 13강은 그런 모델들에 대해서 잘 설명해주셨습니다.
크게 3가지를 살펴봤습니다.
- Probabilitic Spreading Models
- Epidemic models
- modeling using SEIZ model & Independent Cascade Model
Probabilitic Spreading Models
- Random Tree 베이스의 감염 모델입니다. 감염은 시기,시간(h)에 따라 계속 확산할 수도 있고 멈출 수도 있습니다.
- 감염될 확률 p_h를 정의하고, h가 무한대로 발산할 때에 대해서 구해봅니다.
- p_h = 1 - (h만큼 깊이에서 적어도 1개의 node가 감염되었을 확률) , 여사건으로 구함
- 유저가 사진을 보게 되었고, 사진이 확산 되는지 확인하는 실험에 대해서 이 모델을 적용한 예시를 봤습니다.
Epidemic models
- epidemic model들은 전염병을 상상하면 쉽습니다. -> 전염확률과 치료확률이 있습니다.
- SEIR, SIR, SIS model 등이 있습니다. (S : 걸리기쉬운, E : 노출, I : 감염, R : 치료, Z : 면역)
- 각 모델마다 파라미터에 따라 진행이 다르며, virus strength s = beta/delta 입니다.
- Epidemic threshold tau -> 전염/ 치료 보다 큰 값으로 1/ lambda 입니다. (인접행렬의 가장 큰 고유값)
- 루머가 확산되는 상황에 이 SEIZ 모델을 적용한 예시를 봤습니다. -> 트위터를 통해 루머가 확산되는 상황에 대해서 SEIZ 모델로 각 파라미터와 error를 정의하고 그리드서치를 사용해서 error를 최소화했습니다. (추정)
- 노출속도와 감염속도를 파악해서 루머의 경우 빠르게 사실로 받아들여지는(감염)되는 것을 파악했습니다.
Independent Cascade Model
- 위의 모델들과 다르게 랜덤트리가 아니라 그래프에 적용되는 모델입니다.
- 각 edge 마다 확률(weight)p를 가지고 있습니다. (독립시행)
- weight에 대한 전체적인 추정은 어렵기 때문에 노드의 Exposure&Adaption을 정의합니다.
- 이 모델에 대해서는 자세하게 보다는 plot을 그려서 exposure 일 때와, adaption에 대한 커브를 확인했습니다.
이번 강의는 모든것을 가진남자 이홍정님께서 감염병을 예로 들 수 있는Probabilistic Spreading Model에 관해 강의해주셨습니다.
Probabilistic Spreading Models
임이의 노드에서 다른 한 노드로 감염이 진행될 때, 감염 확률이 0보다 크면 전염병이 확산되는것이고, 감염확률이 0이면 전염병이 소멸한다고 말할 수 있습니다.
- 시작노드(임의의 노드)로 부터 depth d의 노드가 감염될 확률 :
임의의 노드에서 depth d의 한 노드가 감염될 확률은 1에서 deph d에 위치한 노드 중 하나의 노드라도 감염될 확률을 빼면 됩니다. 그 확률을 극한으로 보내면,
이고, 는 [0,1]에서monotone non-increasing이고, 에서의 값이 전염병 확산 여부를 결정합니다. - : 전염병 확산
- : 전염병 소멸
Epidemic Models (전염병 모형)
전염병 전파에는 두 개의 파라미터가 있습니다.
birth rate전염될 확률dead rate치료될 확률
전염병 모델에는 대표적으로 SEIR,SIR,SIS Model등이 있습니다.
- SIR : SIR 모형 안에서 진행 상태는 크게 3가지로 구분하여
S(susceptible),I(infected),R(removed)로 나타내게 되는데, 여기서S(susceptible)는 감염대상군으로 전체 모집단 안에서 감염될 가능성이 있는 대상을 일컫습니다. 다음으로 감염대상군에서 감염이 된 집단은I(infected)으로 나타나게 되고 그로부터 사망하거나 회복된 개체의 집단은R(removed)로 나타낼 수 있습니다. SIR모형은 이와 같이 S에서 I로 진행, I에서 R로 진행되는 과정을 가지게 되며, 그 과정에서 질병의 확산을 나타낸 모형이라고 할 수 있습니다. - SEIR : SEIR 모형은 감염대상군
S(susceptible)으로부터 감염되어 감염군I(infected)이 되는 과정에서 질병의 접촉군E(exposed)이라는 단계를 추가한 모형입니다. 즉, 질병에 감염된 후 감염력이 생기는 잠복기가 있는 경우에 연구에 활용될 수 있습니다. 이에 대한 연구는 시간이 지날수록 다양한 분야로 응용되었고 지금도 많은 연구에서 모형으로 활용되며 실제 전염병의 확산 예방에 사용되고 있습니다. - SIS
Independent Cascade Model
edge (u,v)는 확률값을 가지고 있으며, 다른 edge들과 독립적입니다. 하지만, 실제 데이터로부터 이 weight들을 모두 추정하는 것은 굉장히 어렵기 때문에 *새로운 행동(전염)의 전파여부는 이미 행동(전염)이 전파된 주변 노드의 수에 의존하는 것으로 파악합니다.



Epidemic Spreading 에서는,
Probability에 기반해 질병이 퍼져나가게 됩니다.Probabilistic Spreading Model
d: subtree 개수,q: 질병에 감염될 확률 이라고 했을 때,1. Run forever : h→∞lim [a node at depth h] > 0
2. Die out : h→∞lim [a node at depth h] = 0
h를 ∞ 로 보냈을 때, 확률이 0보다 크다면 전염병이 확산된다고 할 수 있고, 확률이 0이라면 전염병이 끝났다고 할 수 있습니다.
따라서, 임의의 node h 에서 감염될 확률 ph 값을 통해 전염병의 지속 여부를 판단합니다.
ph=1−(1−q⋅ph−1)d
(= 1 - 이전 node 에서 나온 subtree 들이 모두 감염되지 않을 확률)
위의 식을 ∞ 로 보냈을 때의 결과물은,
h→∞limph=f(x)=1−(1−q⋅x)d
가 되며, 해당 식에서 x=0 에서의 접선의 기울기 값을 통해 전염병 확산 여부가 결정됩니다.
f′(0)=R0=q⋅d≥1 : epidemic never dies
f′(0)=R0=q⋅d<1 : epidemic dies out
Epidemic Models
Virus Propagation 에는 두 개의 parameter 가 있습니다.
각 node 는 여러 phase 에 도달할 수 있습니다.
위와 같은 phase 에 기반하여, 여러 epidemic model 이 적용됩니다.
1. SIR Model
한 번 감염되어서 치료되면, 더 이상 감염되지 않는 모델입니다.
2. SIS Model
감염되어서 치료되어도, 다시 감염 가능성이 존재하는 모델입니다.
Virus Strength : s=β/δ 로 설정하고, Epidemic Threshold 값을 설정하여 전염병의 확산 정도를 판단합니다.
3. SEIZ Model
phase
S: 루머를 믿지 않는 회의적인 상태여서, spread 하지 않는 상태를 나타냅니다.해당 모델에서는 예측값과 실제값의 차이를 최소화 하는 방향으로 grid search 를 진행해 parameter 를 추정합니다.
Contact rateβ,b,ρ 값을 통해 아래의 식을 도출해 감염 확산 정도를 파악합니다.RSI=E→IS→E=ρ+ϵ(1−p)β+(1−l)b
Independent Cascade Model
edge(u,v) 가 각각 다른 확률값 puv 를 가지고 있는 모델입니다.
이 때 모든 weight 를 추정하는 것은 어려우므로, Exposure Curve 를 통해 판단합니다.
Exposure Curve : Adopting new behavior 의 여부는 이미 behavior 가 전파된 neighborhood node 의 수에 의존하게 됩니다.
추가적으로, persistence 개념이 등장합니다. 그래프의 가장 높은 peak 를 찍은 후에도, 그래프의 곡선이 낮아지지 않는다면 해당 모델은 지속성이 크다고 할 수 있습니다.
모모남 홍정님 띵강 감사합니다 ~