
INTRO

우리는 어떠한 상품을 구매할 때, 주로 낯선 사람들보다 주변 사람들에게 영향을 많이 받습니다. 통계 역시도 68%가 친구들이나 가족들에게 조언을 구한다고 제시하고 있습니다.
그렇다면, 우리는 다음과 같은 마케팅 요소를 생각해볼 수 있을 것입니다.
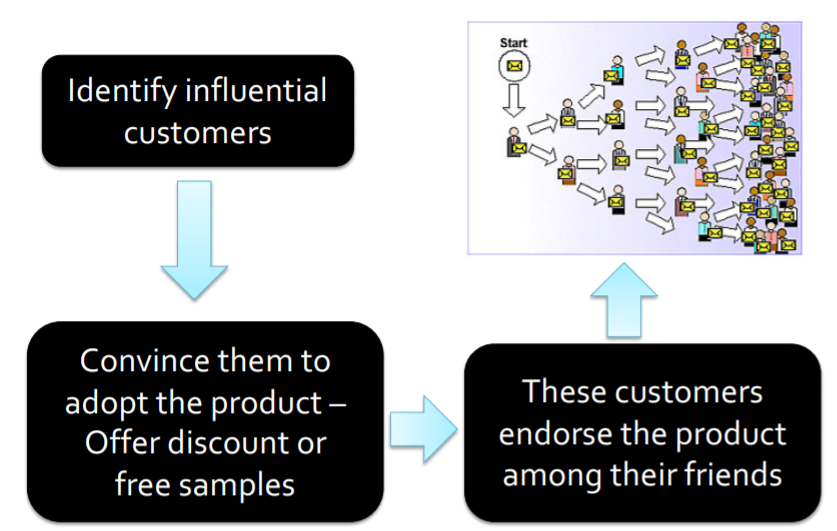
어떠한 사람이 가장 친구들에게 영향을 많이 끼치는가?
한 예로, Kate Middleton effect를 생각해볼 수 있습니다.
"... when she does wear something, it always seems to go on a waiting list."
그녀가 입은 옷은 모두 완판된다는 것으로 그 만큼, 상품을 구매하는데 큰 영향을 끼친다는 것을 알 수 있습니다.
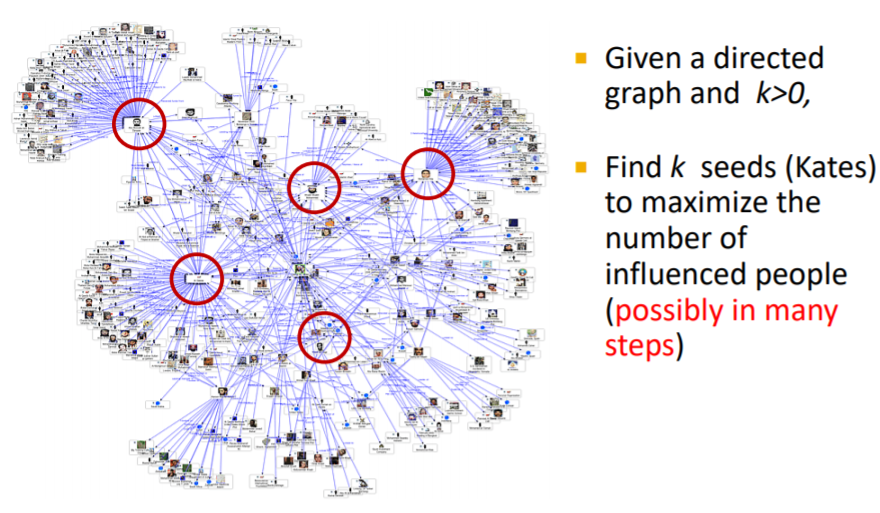
그렇다면, 우리는 Kate와 같이 "Influential Person"을 어떻게 찾을 수 있을까요? Kate와 같은 사람들을 다수 찾는다면, 그만큼 광고 효과를 크게 낼 수 있을 것입니다. (Influence Maximization)
Two Classical Propagation Models
Linear Threshold Model
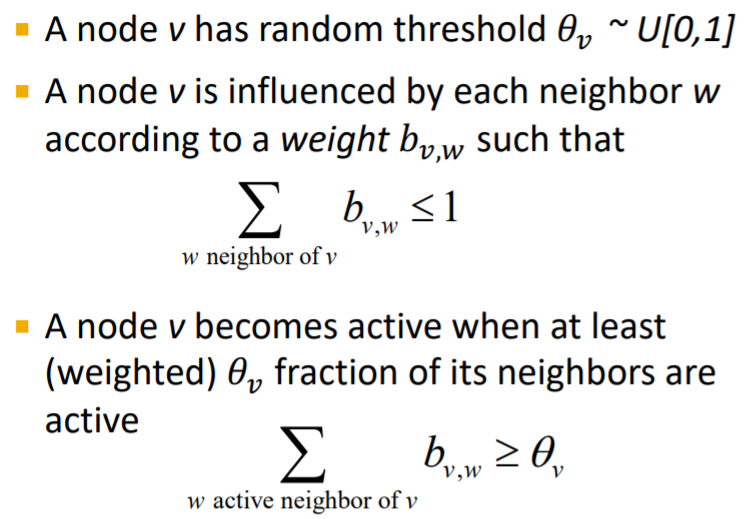
노드마다 임의의 threshold가 있습니다. 이것은 node v가 영향을 받는 정도의 weight를 나타내는 값으로 영향력을 나타냅니다. 예를 들어, 나를 기준으로 친한 친구한테 받은 영향력이랑 학교 선생님한테 받은 영향력이 다를겁니다. 이를 표현한 것이라고 생각하시면 됩니다.
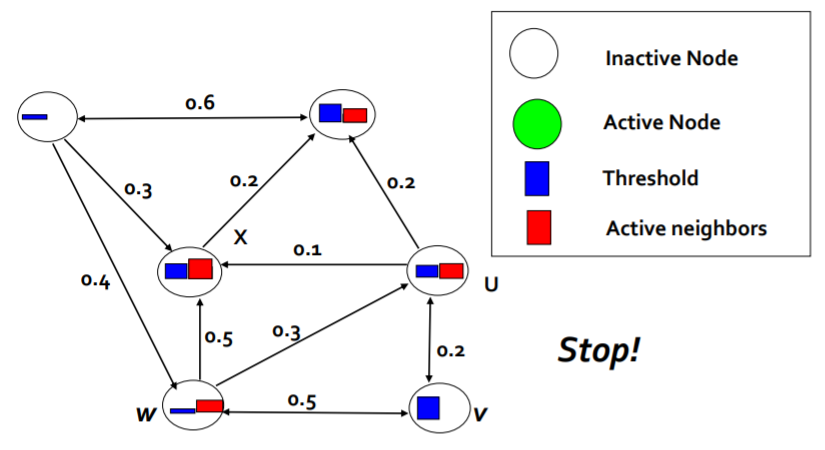
node v부터 시작해봅시다. 각각의 노드들은 앞서 말한 threshold들을 가지고 있고, 그 값보다 크면 영향을 받게 됩니다. node w의 경우, node의 threshold보다 이웃에게 받은 영향이 더욱 크게 나타납니다. (파란색 사각형보다 빨간색 사각형의 크기가 더 큼으로부터 알 수 있습니다.) 따라서 Active Node가 됩니다. 이러한 과정들을 지속적으로 반복하면 Active Node와 Inactive Node를 구분할 수 있게 됩니다.
Independent Cascade Model

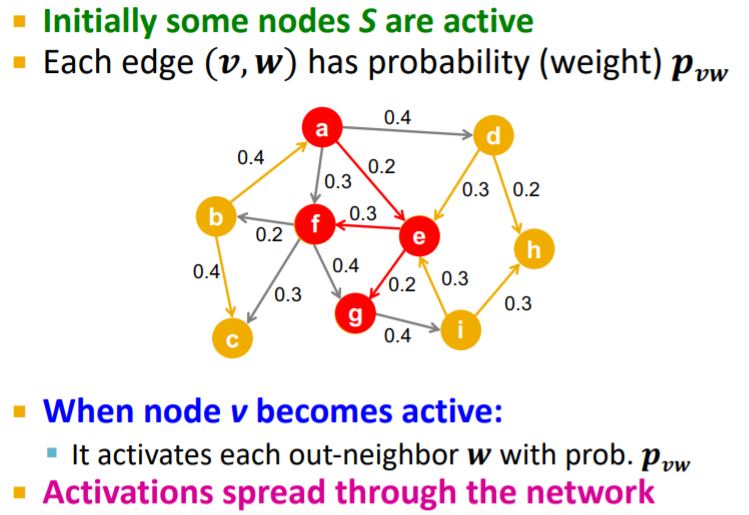
각각의 edge (v, w)는 확률들로 구성되어있으며, node v가 active 되었을 때, node w가 active될 확률들 나타냅니다. 즉, 영향받은 확률을 나타내는 것으로 볼 수 있습니다.
각각의 edge (v, w)는 probability 를 가지고 있다. 이때, 는 node v가 node w에게 영향을 줄 확률이다. 즉, node w가 node v에게 영향을 받아 상품을 살 확률이라고 생각하시면 됩니다.

그러한 작업들을 반복하였을 때, 각각의 subset을 확인할 수 있으며, 영향력이 가장 크게 나타나는 경우 역시 확인해볼 수 있습니다. 위의 그림을 보면 a와 d의 합이 가장 영향력이 크다는 것을 직관적으로 확인할 수 있습니다.
How hard is influence maximization?

정리하면, K개의 node를 찾는 것이며, K개의 node의 subset S가 maximize되어야 한다는 것입니다.
"Influence maximization NP-complete"
NP-complete문제로 해결하지가 쉽지 않습니다. 하지만, approximation algorithm을 활용하여 다음과 같은 문제를 해결할 수 있습니다. 이 algorithm을 사용한다면 최적해 결과의 63%의 효율을 끌어올 수 있습니다.
Greedy Hill Climbing Algorithm

해당 알고리즘은 매시점마다 Si가 최대가 되도록 선택하는 것입니다. 예를 들어, 처음 값을 보면 d가 높은 값을 가지고 있으므로, Si에 d를 추가합니다. 다음 step으로 Si와 합집합하였을 때, 가장 높은 값을 선택하게 됩니다. 이 경우 b이기 떄문에 Si에 b를 추가해줍니다.
이러한 과정을 계속해서 반복하여 최적값을 찾아가는 것이 해당 알고리즘이라고 생각하시면 됩니다.

해당 함수는 두가지 특성이 나타나게 됩니다.
- f is monotone
- f is submodular
Prove 1: our f(S) is submodular

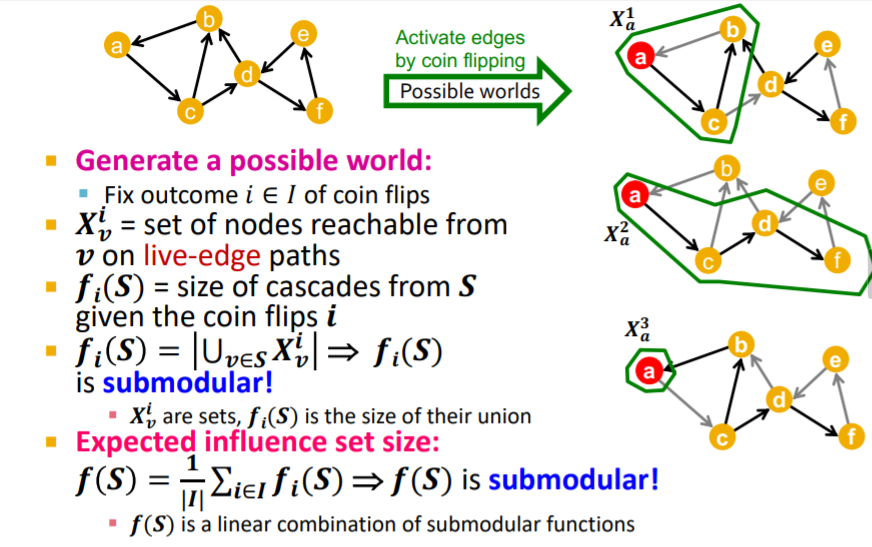
T가 S를 포함하고 있다고 가정해봅시다. 그렇다면 u라는 순수영역을 더욱 보존하고 있는 경우는 당연히 S가 될 것입니다. 그림에서 녹색으로 채워진 부분이 S이며, 녹색과 파란색으로 채워진 부분이 T입니다. 해당 집합들과 u간의 차집합을 구했을 때, S인 경우가 u의 면적이 더 많이 남아있음을 알 수 있습니다.
Principle of deferred decision
f(S)를 확률적으로 접근했기 때문에 우리는 f(S)에 해당하는 parallel possible worlds를 만들 수 있고, 이걸 average함으로써 우리의 알고리즘(무작위 알고리즘)에 신뢰를 줄 수 있습니다.
Prove 2: Hill Climbing gives near-optimal solutions

해당 식의 증명과정은 이곳은 참고하면 됩니다!
Greedy algorithm is Slow
위의 모든 과정들을 생각해봤을 때, 연산속도가 매우 느리다는 것이 큰 단점인 것을 파악할 수 있습니다. 우리는 k만큼의 영향력있는 사람들을 알길 원하며, 모든 node에 대해서 iteration을 진행해야 합니다.
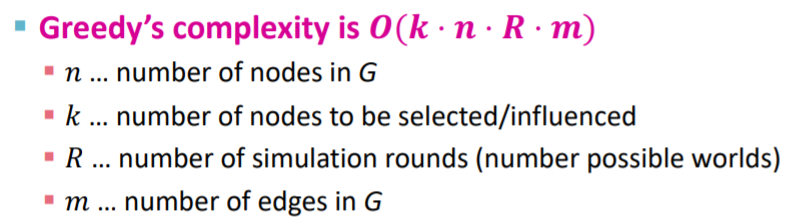
Sketch-based Algorithms
그리디 알고리즘을 수행할 경우, 많은 시간이 소요됨을 확인할 수 있었습니다. 따라서, 연산시간을 줄이기 위해서 Sketch-based Alogrithms을 사용하고자 합니다. 이 모델은 기존의 시간복잡도 O(M)을 O(1)로 줄일 수 있습니다. (m = number of edges)
- Take a possible world G(i)
- Give each node a uniform random number from 0~1
- Compute the rank of each node v, which is the minimum number among the nodes that v can reach
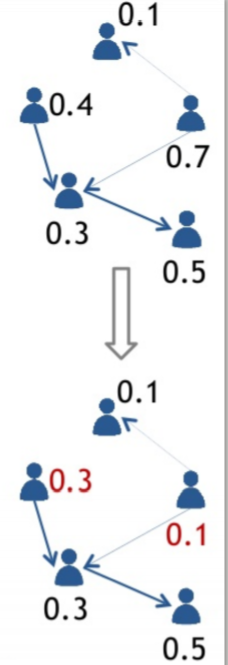
여기서의 핵심 아이디어는 node v가 많은 node들과 연결되어있다면, 그 만큼 rank가 작을 것이라는 것입니다. 따라서, 해당 rank 정보를 활용하여 영향력을 추정해볼 수 있게 되는 것입니다.
하지만, 이러한 추정은 물론 불안정합니다. 하지만, 다수의 random number와 rank를 부여한다면 추정의 불안정성을 어느정도 개선할 수 있습니다.
2개의 댓글
어떤 결정을 할 때, 주변의 영향을 많이 받게 됩니다. 이렇게 영향을 끼치는 사람 중, 가장 영향력 있는 사람 (Influential Person) 을 찾는 방법에 대해 공부했습니다.
Propagation Model
- Linear Threshold Model

node 마다 가지고 있는threshold값이 다른 모델입니다.
neighborhood 로 부터 받게 되는 영향력이 기존의 threshold 보다 커지게 되면, active node 로 바뀌게 됩니다. 과정이 지속적으로 반복되어 Inactive / Active node 로 결정됩니다.
- Independent Cascade Model

edge(u,v) 가 probability, 즉 영향을 줄 확률로 이루어진 모델입니다.
random walk 로 과정이 진행되며, 지속적으로 과정이 반복된 후에 각 node 에 대한 subset S 가 생성됩니다.
가장 영향력이 큰 node 를 찾는 것이므로, subset S 의 크기가 최대가 되는 k를 찾는 것이 목표입니다.
computation problem 때문에 Algorithm 을 사용해 k를 찾습니다.
Greedy Hill Climbing Algorithm
매 시점마다 Si가 최대가 되도록, 최적의 선택을 진행합니다.
가장 영향력이 있는 node 를 담고, 이후 합쳤을 때 영향력이 커지는 node 를 담게 됩니다. 이러한 과정을 계속적으로 반복해 최적 값을 찾습니다.
Greedy Hill Climbing Algorithm 을 진행하기 위해서는,
f(S) 가 1. monotone (단조 증가)이어야 하며, 2. submodular (추가되는 node 에 영향을 덜 끼치도록 부분집합 구성...?ㅎㅎ...) 이어야 합니다.
그렇지만 Greedy Hill Climbing Algorithm 의 시간복잡도는 (k개의 set, n개의 node, R번 시행, m개의 edge) 이며, 모든 node 에 대해 iteration 을 진행해야 하기 때문에 매우 느리다는 단점이 있습니다.
따라서 연산량을 에서 로 줄인, Sketch-based Algorithm 이 등장합니다.
graph G 의 node 들에 random 으로 Unif(0,1) 값을 부여하고, node가 도달할 수 있는 node 중 가장 작은 값으로 바꾸어 줍니다. 이를 통해 rank 를 계산합니다. node의 숫자가 작을수록, 많이 도달할 수 있다는 것을 의미합니다.
딥러닝을 멋지게 다루는 남자 이홍정님 띵강 감사합니다 ~


14강. Influence Maximization in Networks
홍정님은 대단하시기 때문에 연강으로 띵강을 해주셨습니다. 발표자님은 이 강이 더 재밌었다고 하십니다.
이번 14강은 어떤 사람이 우리에게 영향을 미칠까?에 대한 강의입니다. 지디가 입은 옷, 발매하는 신발 등등은 완판되어서 구하기가 어려운데요. 이렇게 지디만큼 우리 구매에 영향을 주는 사람을 찾아보는 강의 입니다.
Two Classical Propagation Models
이 propagation(전파) 모델에는 두 가지 종류가 있습니다. Linear Threshold Model 과 Independent Model 입니다.
Greedy Hill Climbing Algorithm
반복해서 S에 값을 추가하는 이 함수 f는 두가지 성질이 있습니다. ->
monotone,submodular(한국어도 서브모듈성)1. submodular
강의 설명에 덧붙이자면, 서브모듈성은 다음과 같이 직관적으로 이해됩니다.
2. Hill Climbing gives near-optimal solutions
강의내용에 설명되어있고, 증명은 생략했습니다.
-> 하지만 Greedy algoritm 도 연산속도가 느린것 이 단점이라고 합니다. (모든 노드에 대해서 반복해서)
-> 따라서 연산량을 줄이는 Sketch-based algorithm을 사용합니다.
Sketch-based algorithm