
작성자 : 김태욱
Contents
- Intro
- Limitations of conventional GNNs in capturing graph structure
- Vulnerability of GNNs to noise in graph data
- Open questions & Future directions
0. Intro
핵심 아이디어 : 로컬 네트워크 환경을 기반으로 노드 임베딩 생성
neighbor aggregation의 아이디어를 기반으로 노드는 신경망을 사용하여 neighbor로부터 정보를 수집합니다.
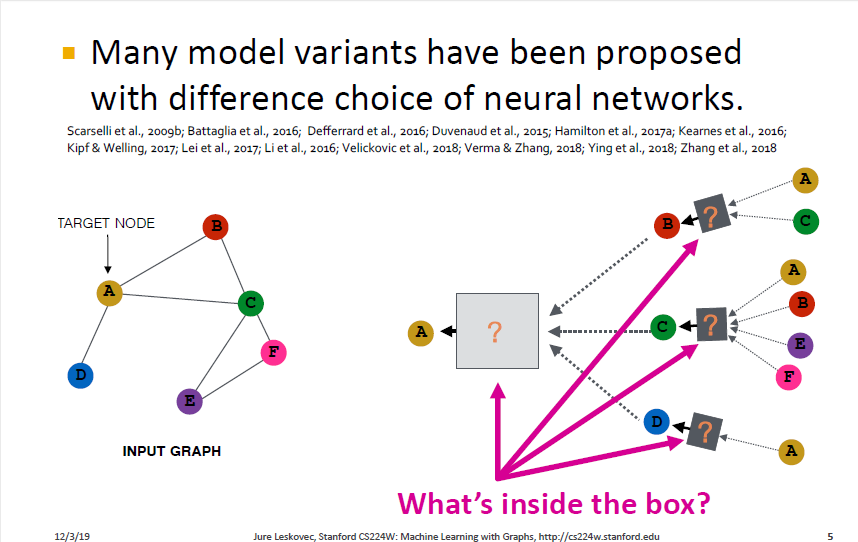
다양한 신경망 선택에 따라 다양한 모델 변형이 제안되며 모델에 따라 박스 안에 들어가는 내용물이 달라집니다.
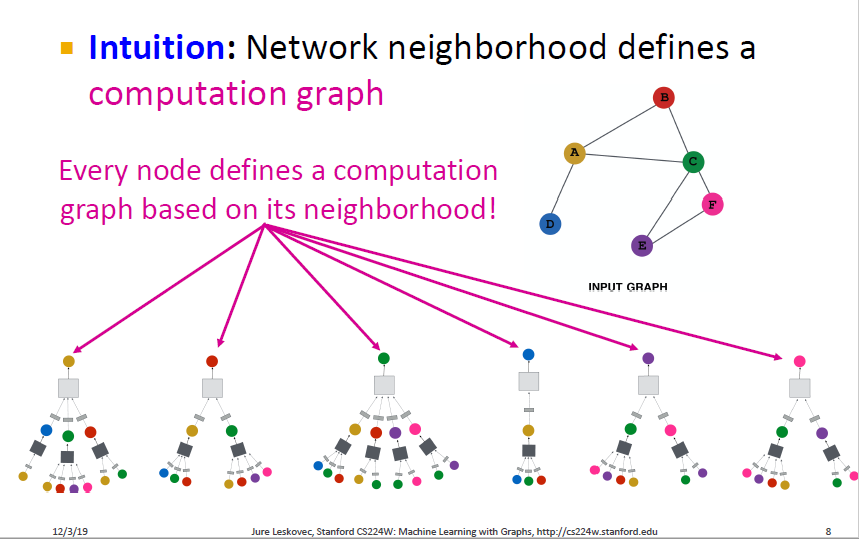
각 노드는 이웃에 따라 computation graph를 정의하고 neighbor aggregation을 통해 노드 임베딩을 구합니다. node representation을 구한 후 해당 graph의 노드들을 더하거나 평균내는 방식(Pooling)으로 하나의 graph representation을 구하게 됩니다.

위의 그림과 같이 GNN을 활용하여 많은 SOTA성능을 내기도 했지만 GNN에는 한계가 존재하고 이번 강의에서 그 한계에 대해 배우게 됩니다.
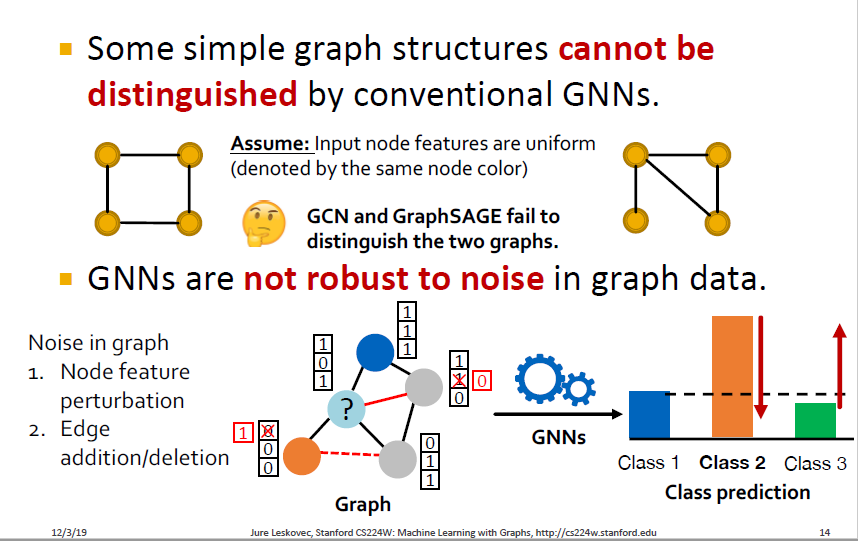
GNN에는 크게 2가지 한계점이 존재합니다.
1. 기존의 GNN으로는 일부 간단한 그래프 구조를 잘 구분하지 못합니다.
2. GNN은 그래프 데이터의 노이즈(node feature의 변화, edge의 추가/삭제)에 robust하지 못합니다.
1. Limitations of conventional GNNs in capturing graph structure
Graph Isomorphism
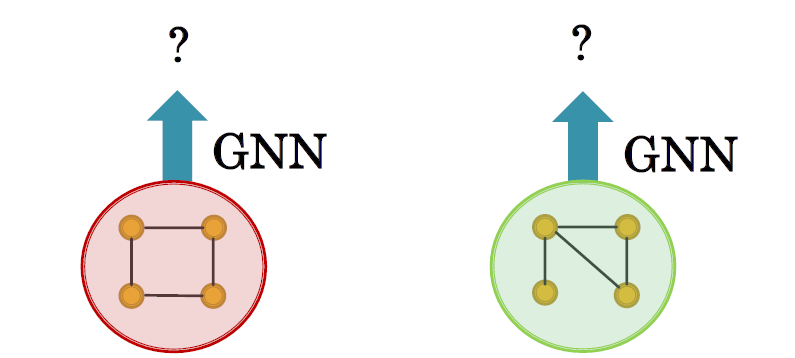
GNN은 위 그림의 두 그래프를 잘 구분해 내지 못할 수 있습니다. 이러한 문제를 완벽하게 해결할 수 있는 다항식 알고리즘은 없기 때문에 GNN이 완벽하게 구분하지 못할 수 있으며 이를 해결하기 위해선 그래프의 설계부터 신경써야 합니다.
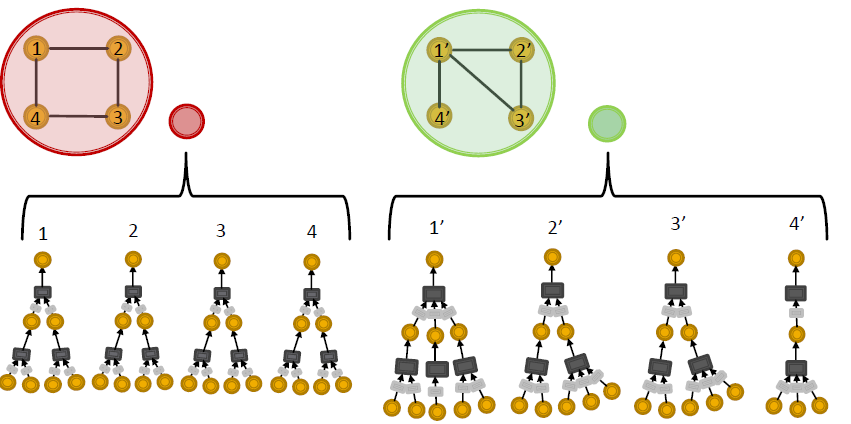
왼쪽의 그림을 보면 4개의 노드는 다 다른 노드지만 computation graph를 보면 모두 동일하며 각 노드가 다르다는것을 GNN에 이해시키는 것은 불가능합니다. 반면 오른쪽의 그래프를 보면 노드간의 차이가 존재합니다.
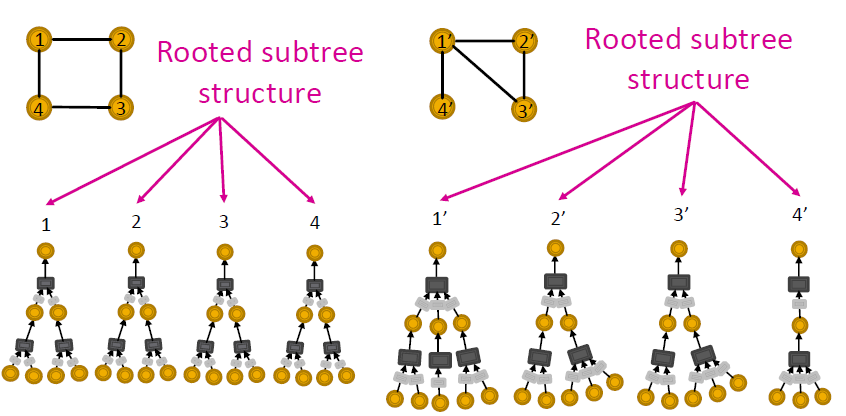
graph representation을 위해 neighbor aggregation을 통한 node representation을 하면 두 개의 다른 노드를 가진 그래프가 생깁니다. 하지만 이러한 aggregating 과정에서 mean pooling이나 max pooling을 사용하게 되면 두 그래프는 같은 결과값이 나오게 됩니다. 이를 해결하기 위해 injective function을 aggregate function로 사용합니다.
injectivity
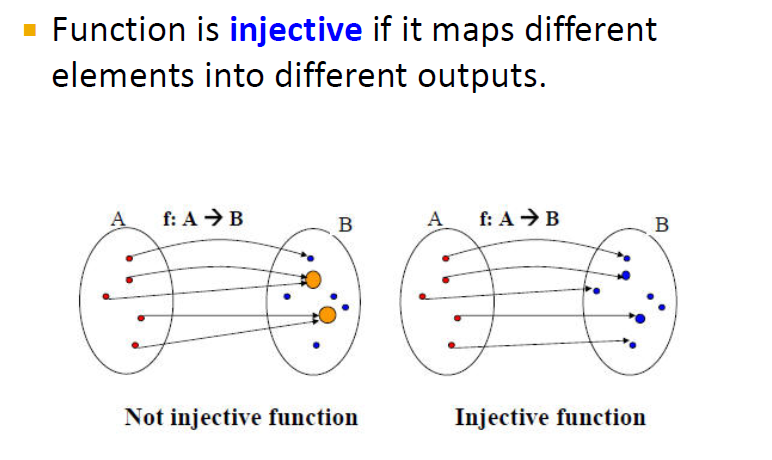
하나의 output에 하나의 element를 mapping하는 것으로, 이를 통해 node의 subtree가 다르면 node representation 또한 달라지게 됩니다. 여기서 각 트리의 층마다 injective function을 적용해 줍니다.
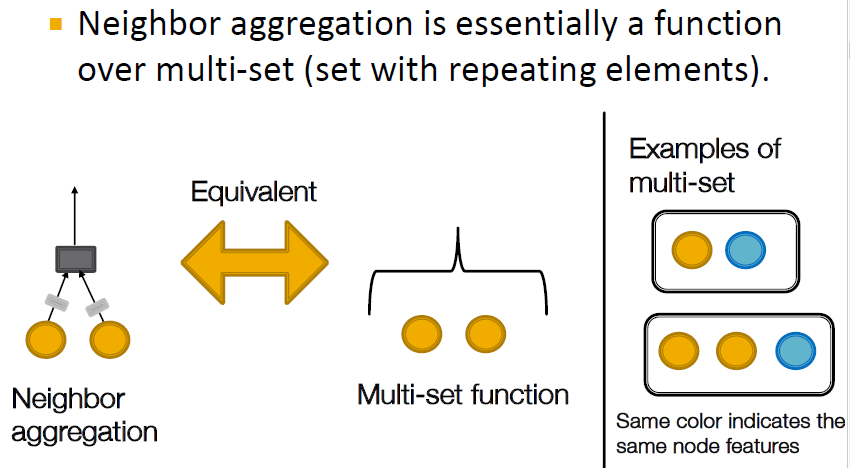
Neighbor aggregation은 multi-set로 이루어지는데, 여기서 multi-set는 set에서 중복요소를 추가한 것입니다. 이를 활용함으로써 neighbor aggregation을 더욱 잘 표현할 수 있습니다.
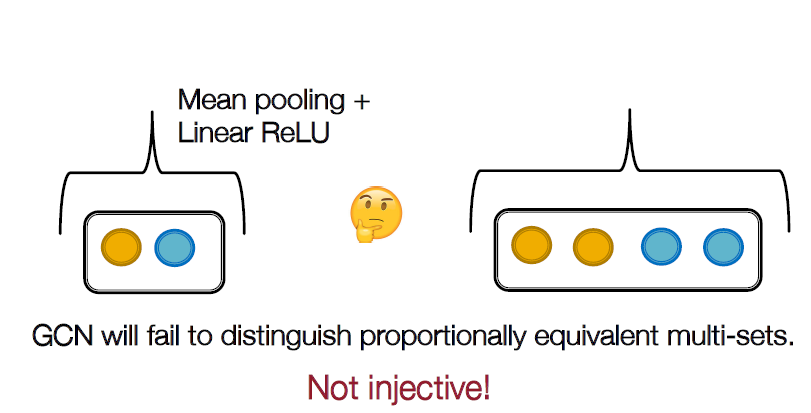
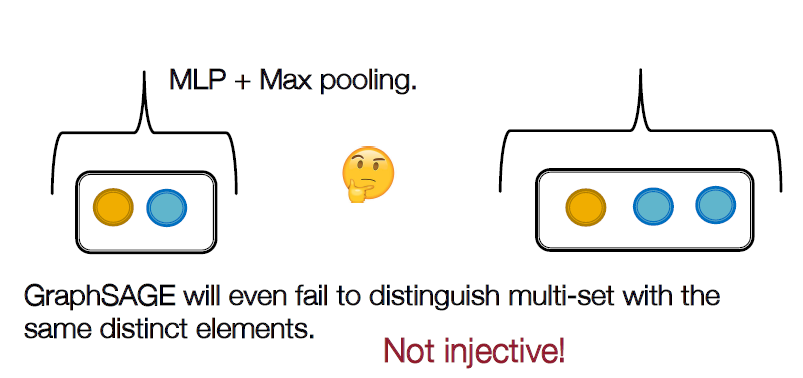
GCN과 GraphSAGE에는 multi-set를 적용하더라도 injective하지 않습니다. GCN에서 mean pooling을 하는 경우 노란색 1개, 파란색 1개인 경우와 2개,2개인 경우 모드 mean을 한다면 0.5 * 0.5가 되어 같은 결과가 나옵니다. GraphSAGE에서는 max값만 뽑기 때문의 각 노드의 개수는 중요하지 않습니다.
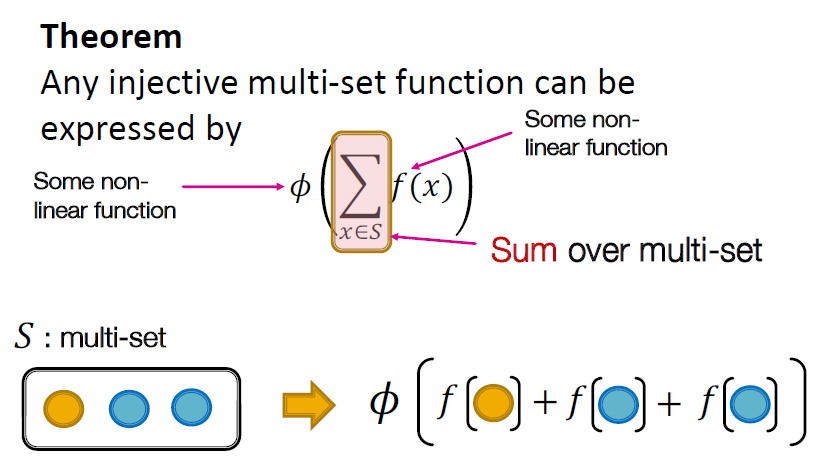
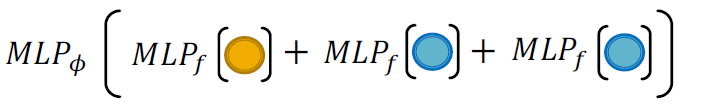
injective mult-set function을 표현하면 위 그림과 같습니다.
Graph Ismorphism Network (GIN)
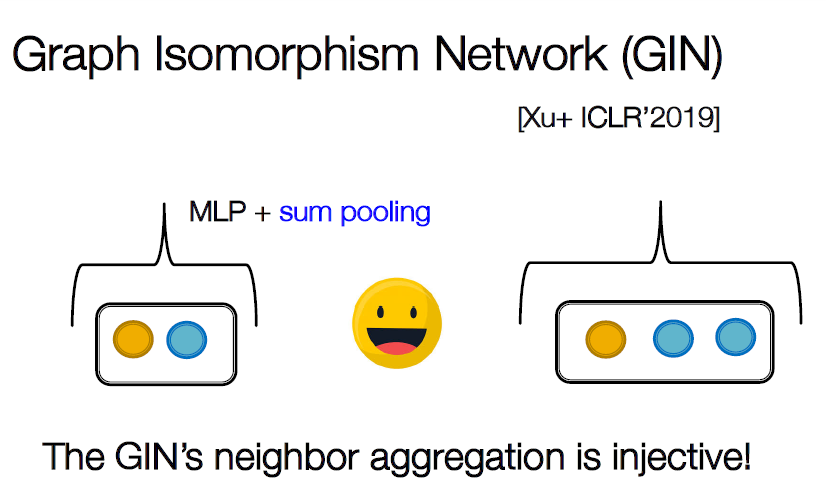
위의 예시를 GCN과 GraphSAGE는 구별 할 수 없지만 GIN의 Sum pooling을 사용하면 구분할 수 있습니다.
Weisfeiler-Lehman (WL) Graph Isomorphism Test와 마찬가지로 GIN은 동형 그래프를 구별하는 좋은 능력을 가지고 있는데 그 방법은 아래와 같습니다.
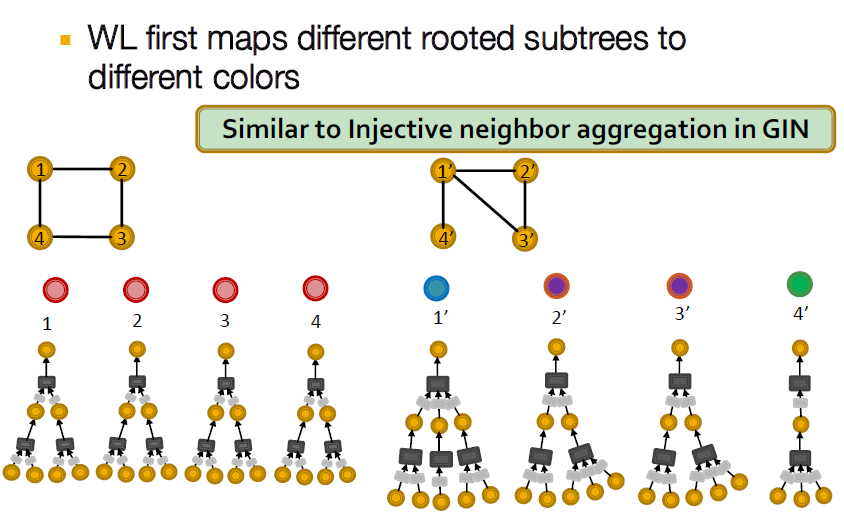
먼저 root로부터 subtree를 하나씩 내립니다. 이때, node간의 다름이 확인되면 거기서 멈추고 같은 개수의 subtree를 가지고 있다면 이를 계속 진행해 시작 노드의 색을 구분합니다.
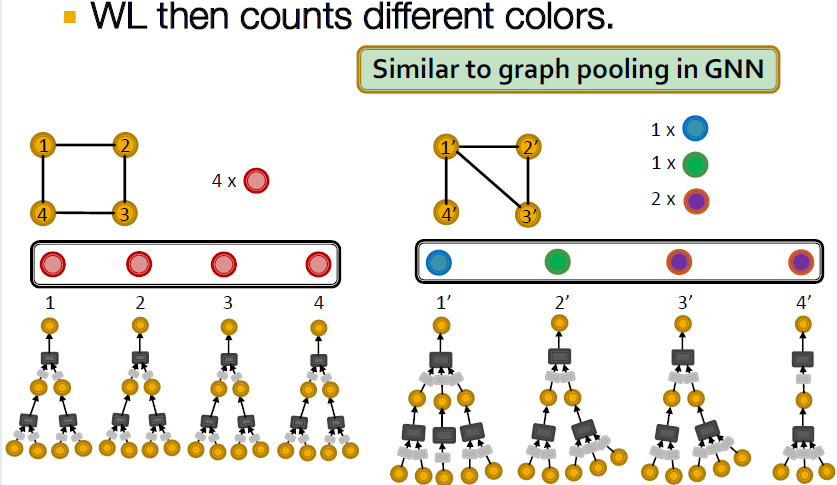
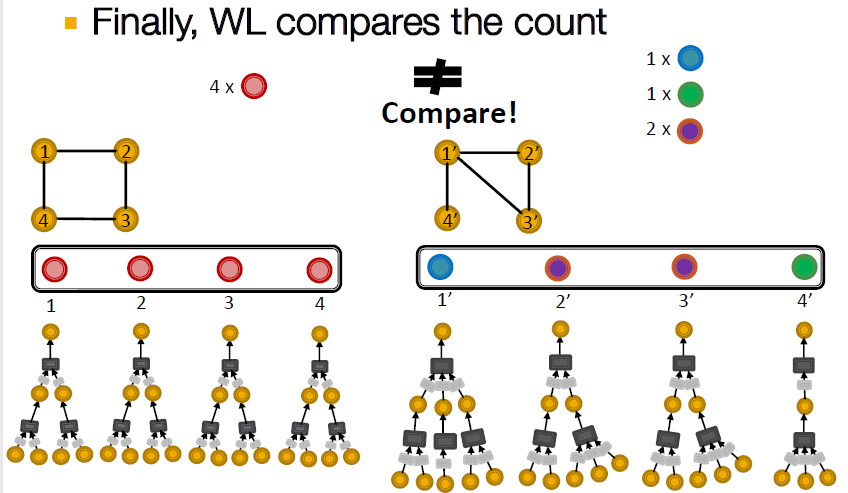
이후 각 그래프에서 같은 색의 노드 개수를 세어주고 이를 바탕으로 그래프를 이루는 노드의 개수를 구분합니다. 그 결과가 동일하다면, 두 그래프는 isomorphism 하다고 할 수 있습니다.

이렇게 GIN은 좋은 성능을 보여주지만, 위 그림과 같이 모든 노드가 같은 수의 subtree를 가지는 경우에는 WL로 구분할 수 없습니다.
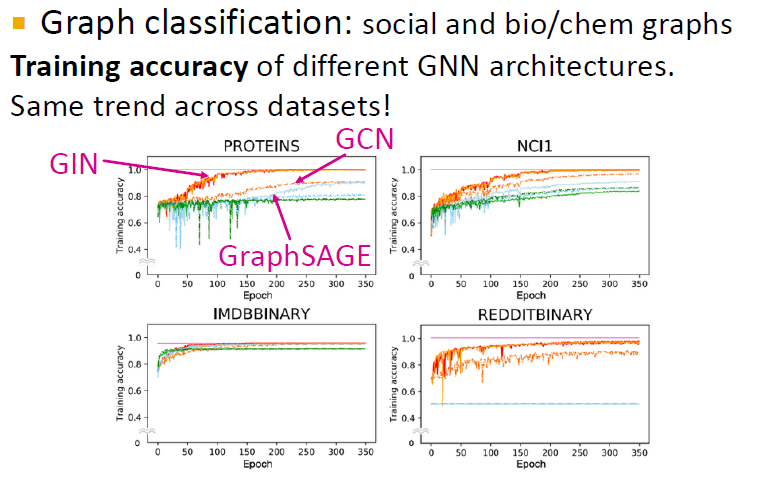
다른 모델들과 비교해 좋은 성능을 보여줍니다.
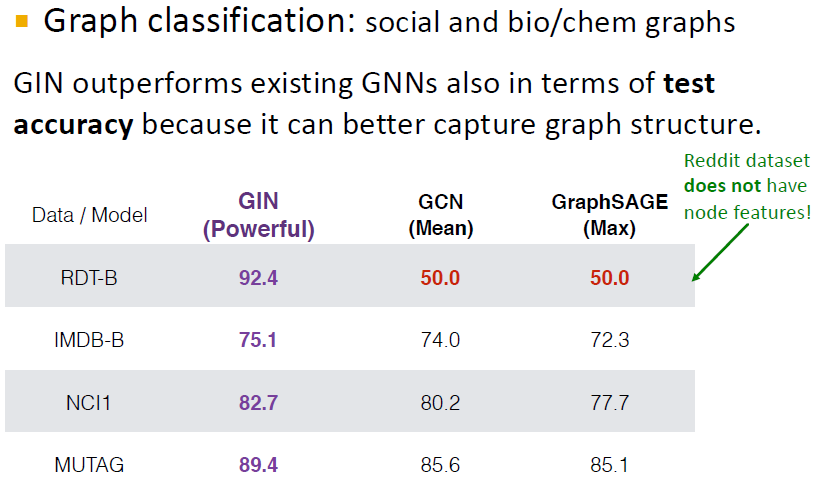
node feature가 존재하는 경우에는 성능의 차이가 크지 않다고 합니다.
Summary of the first part
-
기존의 GNN은 non-injective neighbor aggregation을 사용하기 때문에 구별하는 능력이 떨어짐
-
GIN은 injective neighbor aggregation을 사용하기 때문에 성능은 WL graph isomorphism test만큼 좋음
-
GIN은 graph classification에서 SOTA의 성능을 보임
2. Vulnerability of GNNs to noise in graph data

DNN은 데이터 교란에 취약합니다. 눈에 보이지 않는 변화만 주더라도 예측 결과에 변화를 주며 이는 이미지 뿐만 아니라 검색엔진, 추천시스템, sns 등 여러 분야에서 쉽게 발생합니다.
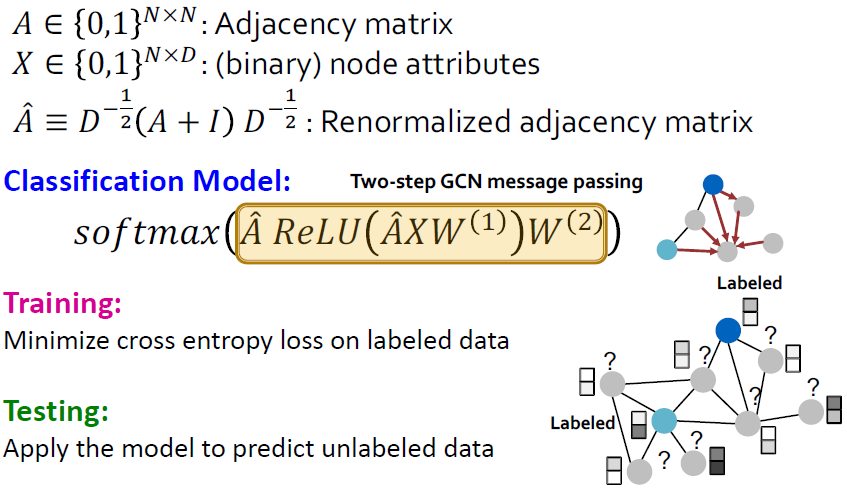
위 그림은 GCN을 활용한 semi-supervised node classification에서 비어있는 label을 채워 넣는 문제입니다.

실생활에서 attack possibilities 하는 방법에는 두가지가 있습니다.
- Direct attack
- target node를 직접적으로 변경하는 방법으로, target의 feature를 변경한 뒤 target에 대한 연결을 해줍니다. 이는 target으로부터의 연결을 제거함으로써 해결할 수 있습니다.
- Indirect attack
- target을 follow한 후 attacker의 feature를 변경합니다. 이후 attacker의 연결을 늘려 spam farm을 만들어줍니다. 이는 attacker로부터의 연결을 제거함으로써 해결 가능합니다.
Mathematical Formulation of Attack

이 공식은 타겟노드에 대한 예측된 라벨의 변화를 최대화하는 수정된 그래프를 찾는것이 목적입니다.이 공식에는 두 가지 주요 공격 유형이 있는데, adjacency matrix A를 변경하는 방법과 node feature X를 변경하는 방법이 있습니다.
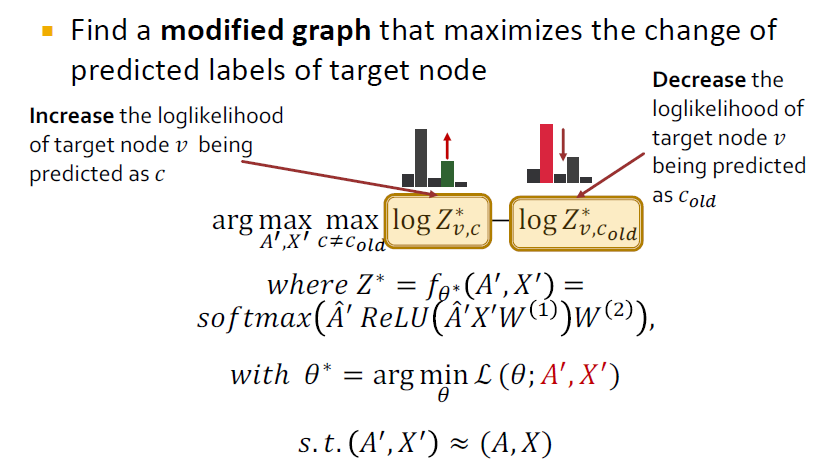
타겟노드 v가 c로 예측될 loglikelihood을 높이는 것과 변경되기 전의 c_old로 예측되는 대상 노드 v의 loglikelihood을 줄여줍니다.
공격 전에 노드 v는 c_old에 속합니다.공격 후에는 c_old에 속하는 노드 v의 확률이 낮아지고 동시에 c에 속하는 노드 v의 확률이 증가합니다.
즉, 공격 전후에 서로 다른 범주에 속하는 노드 v의 확률이 변경되어 공격이 성공합니다.
여기서 GCN은 수정 된 그래프에서 훈련 된 후 대상 노드의 레이블을 예측하는 데 사용됩니다.
이렇게 변경된 그래프는 원래의 그래프에 가까워야 합니다.
Tractable Optimization
최적의 해를 정확히 구하는 것은 불가능한데, 그 이유로는 두 가지가 있습니다.
1. Graph modification은 이산적이기 때문에 최적화를 위한 gradient descent를 사용할 수 없음
2. 과정의 일부인 GCN을 다시 학습시키는데 비용이 많이 듬
이를 해결하고 근사 솔루션을 얻기 위해 그래프의 수정을 단계적으로 해가는 방법과 ReLU를 제거하여 GCN을 단순화 하는 방법등 몇가지 간편 추론(heuristics)이 제안되었습니다.
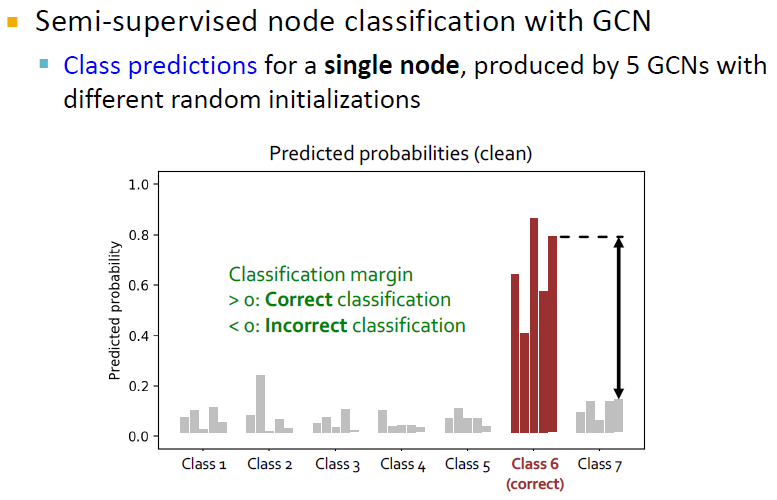
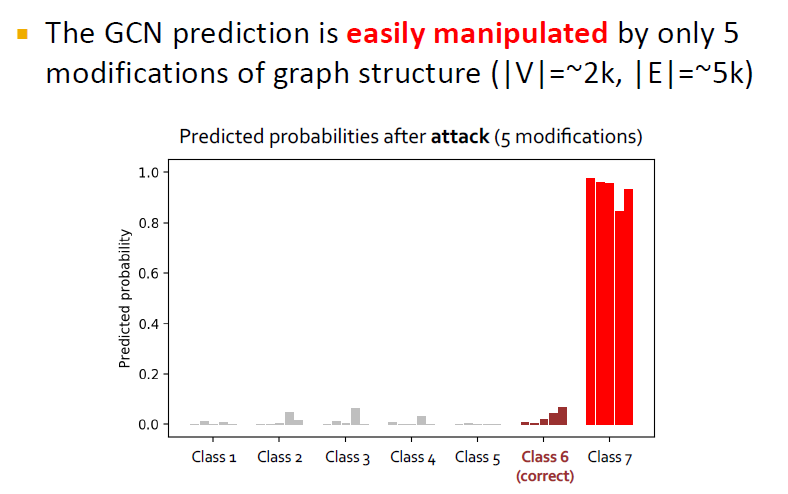
Summary of the second part
GNN은 robust하지 못하고 공격에 취약합니다.
3. Open questions & Future directions
향후 화학과 생물학 등 과학 도메인에 GNN을 적용하기 위해 연구할 예정입니다.
현재 직면한 과제로는
1. 라벨링된 데이터의 부족
- 라벨링에는 비싼 실험이 필요하고 라벨링된 데이터 부족으로 인해 모델이 오버피팅 됨
- 실제 테스트 케이스와 학습한 것이 많이 달라 분포 이탈 예측이 발생함(일반적으로 성능이 좋지 않음)
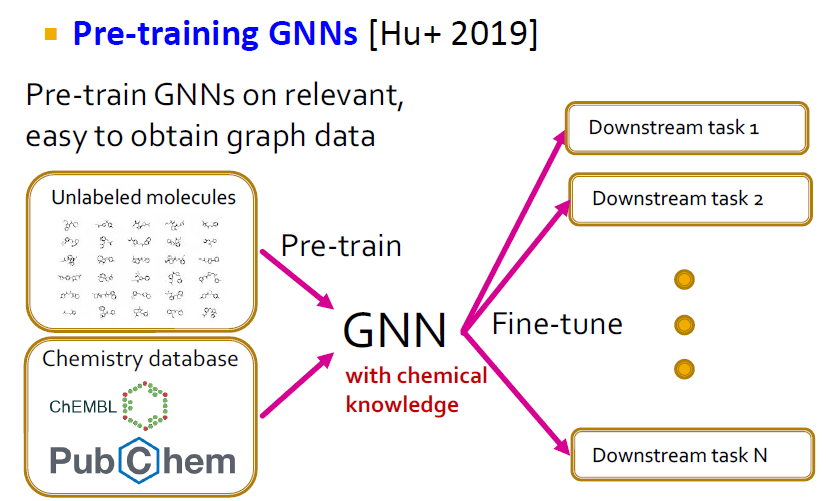

과학 분야에서의 pre-training GNN이 연구되고 있으며 공격이 있으면 방어가 있듯 GNN을 robust하게 만들기 위해 노력하고 있음

GNN은 2가지 한계가 존재합니다.
1. 기존의 GNN으로는 일부 간단한 그래프 구조를 잘 구분하지 못합니다.
2. GNN은 그래프 데이터의 noise 에 robust 하지 못합니다.
1. Graph Structure
모든 node 는 각기 다르지만,
computation graph를 구축해 보았을 때 같은 representation 을 나타낼 수 있습니다. 또한aggregation과정에서, mean/max pooling 을 적용할 시 같은 결과를 나타내기도 합니다.이를 해결하기 위해
injective function을 사용합니다.하나의 output 에 하나의 element 를 mapping 하는 것 (일대일 대응) 으로, node의 subtree가 다르면 node representation 또한 달라지게 만들어 줍니다.
또한
multi-set을 통해 aggregation 을 표현합니다.Graph Ismorphism Network (GIN)
GIN 은 Weisfeiler-Lehman (WL) Graph Isomorphism Test 와 유사하게, 동형 그래프를 쉽게 구분할 수 있습니다.
root 에서 subtree 를 내려서, computation graph 를 구축한 뒤 색을 부여해 node 를 구분합니다. 같은 색의 node 개수를 세어
isomorphism을 결정합니다.하지만 이 경우, 개수만으로 결정하는 것이기 때문에, node feature 가 존재하는 경우 효과적이지 못하다고 합니다.
2. Noise in Graph
GNN 의
attack possibility는 크게 두 가지가 있습니다.1. Direct Attack : Target node 의 feature / connection 변경
2. Indirect Attack : Target node 의 neighborhood (= 혹은 영향을 주는 node) feature / connection 변경
attack possibility 의 Mathematical Formulation 은 다음과 같습니다.
Target node 의 예측된 라벨의 변화를 최대화하는 modified graph 를 찾는 것이 목적입니다. 1. adjacency matrix A 를 변경하는 방법, 2. node feature X 를 변경하는 두 가지 주요 공격 유형이 있습니다.
argmax(max(target node v 가 c 로 예측될 loglikelihood - target node v 가 cold 로 예측될 loglikelihood)), (c=cold) 로 objective function 을 설정하여, 공격 전후에 서로 다른 범주에 속하는 노드 v의 확률이 변경되어 공격이 성공하게끔 만들어 줍니다.
띵강 감사감사 함니다 ~